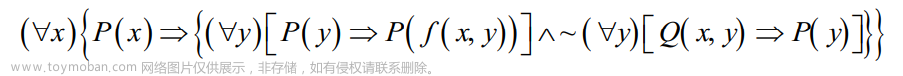各位CSDN的uu们你们好呀,今天,小雅兰来复习一下之前学过的知识点,也就是导数与微分的总复习,依旧是高等数学的内容,主要是明天就要考高等数学了,哈哈哈,下面,让我们一起进入高等数学的世界吧
一、导数
二、求导数
三、求高阶导数
四、微分
题型1:与导数定义有关问题
题型2:求复合函数导数或微分
题型3:求参数方程的导数或微分
题型4:求隐函数的导数或微分
题型5:求幂指函数的导数或微分
题型6:求分段函数的导数
题型7:求高阶导数
题型8:对数求导法
一、导数

 二、求导数
二、求导数

 三、求高阶导数
三、求高阶导数

四、微分



那知识点的简要复习就到这里了,关键的是题目
题型1:与导数定义有关问题

 这里有一个更一般性的结论,感兴趣的可以去推导一下
这里有一个更一般性的结论,感兴趣的可以去推导一下


对于这种判断题,我们一般采用举反例的方法




题型2:求复合函数导数或微分





这里要尤为注意:e是一个常数,它的导数为0,绝不能把它的导数认为成e了



题型3:求参数方程的导数或微分






题型4:求隐函数的导数或微分
直接法




题型5:求幂指函数的导数或微分




题型6:求分段函数的导数






题型7:求高阶导数


 这个题目需要用到直接法和数学归纳法
这个题目需要用到直接法和数学归纳法


间接法 

莱布尼茨公式法:看到求两个函数的乘积的高阶导数

题型8:对数求导法



这个计算就自己下去计算一下
好啦,小雅兰今天复习的高等数学的内容就到这里啦,明天高数考试冲冲冲呀!!!文章来源:https://www.toymoban.com/news/detail-788094.html
 文章来源地址https://www.toymoban.com/news/detail-788094.html
文章来源地址https://www.toymoban.com/news/detail-788094.html
到了这里,关于导数与微分总复习——“高等数学”的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!