这篇具有很好参考价值的文章主要介绍了关于吴恩达机器学习中反向传播的理解。希望对大家有所帮助。如果存在错误或未考虑完全的地方,请大家不吝赐教,您也可以点击"举报违法"按钮提交疑问。
title: 关于吴恩达机器学习中反向传播的理解
date: 2022-04-12
categories: 数学
mathjax: true
tags:
- 机器学习
- 线性代数
原文
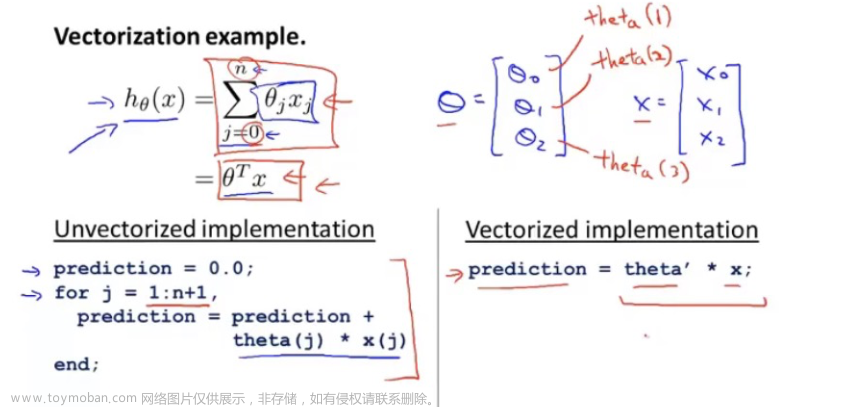
在机器学习视频反向传播章节中:
我们用 \(\delta\) 来表示误差,则: \(\boldsymbol\delta^{\left(4\right)}=\boldsymbol a^{\left(4\right)}−\boldsymbol y\) 。我们利用这个误差值来计算前一层的误差:
\(\boldsymbol\delta^{\left(3\right)}=\left(\boldsymbol\Theta^{\left(3\right)}\right)^T\boldsymbol\delta^{\left(4\right)}\cdot g^\prime\left(\boldsymbol z^{\left(3\right)}\right)\) 。其中 \(g^\prime\left(\boldsymbol{z}^{\left(3\right)}\right)\) 是 \(S\) 形函数的导数,
\(g^\prime\left(\boldsymbol z^{\left(3\right)}\right)=\boldsymbol a^{\left(3\right)}\cdot\left(1−\boldsymbol a^{\left(3\right)}\right)\) 。而 \(\left(\boldsymbol\Theta^{\left(3\right)}\right)^T\boldsymbol\delta^{\left(4\right)}\) 则是权重导致的误差的和。
问题
\[\boldsymbol\delta^{\left(3\right)}=\left(\boldsymbol\Theta^{\left(3\right)}\right)^T\boldsymbol\delta^{\left(4\right)}\cdot g^\prime\left(\boldsymbol z^{\left(3\right)}\right)
\]
看到这道算式时我百思不得其解。为什么凭空会有转置?
在我自己推一遍之后,发现原公式中可能有些不严谨的地方,所以在此阐述我的理解,欢迎大家指正:
前提
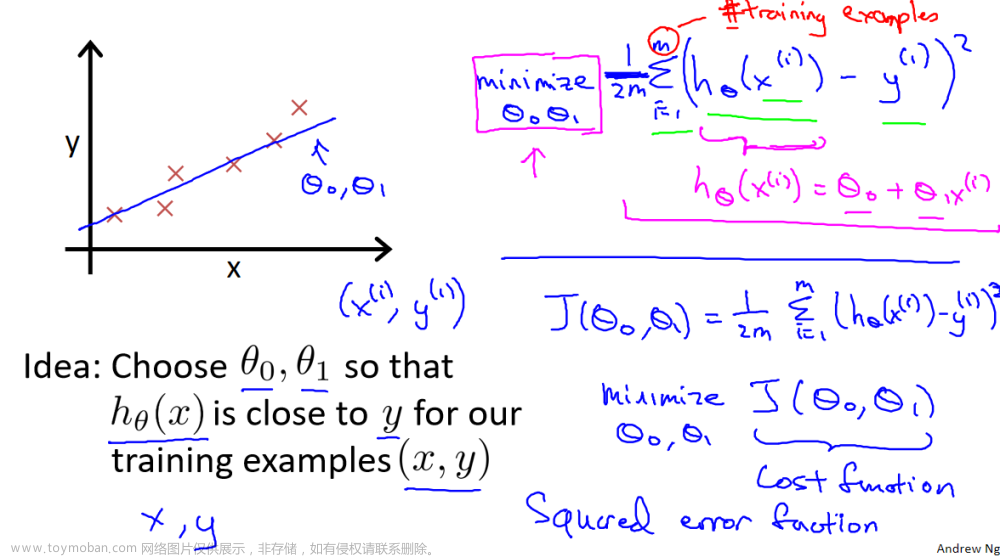
对数似然代价函数: \(J\left(\Theta\right)=y\ln h_\Theta\left(x\right)+\left(1-y\right)\ln\left(1-h_\Theta\left(x\right)\right)\)
估计函数: \(h_\Theta\left(x\right)=\sum_i\Theta_ix_i=
\begin{bmatrix}\Theta_1&\Theta_2&\cdots&\Theta_n\end{bmatrix}
\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}\)
Logistic激活函数: \(g\left(x\right)=\frac1{1+{\rm e}^{-x}}\)
此外激活函数导数为: \(g^\prime\left(x\right)=g\left(x\right)\left[1-g\left(x\right)\right]\)
我的理解
flowchart LR
x1--"(Θ<sub>1</sub><sup>(1)</sup>)<sub>1</sub>"-->z12
x1--"(Θ<sub>1</sub><sup>(1)</sup>)<sub>2</sub>"-->z22
x2--"(Θ<sub>2</sub><sup>(1)</sup>)<sub>1</sub>"-->z22
x2--"(Θ<sub>2</sub><sup>(1)</sup>)<sub>2</sub>"-->z12
a12--"(Θ<sub>1</sub><sup>(2)</sup>)<sub>1</sub>"-->z13
a12--"(Θ<sub>1</sub><sup>(2)</sup>)<sub>2</sub>"-->z23
a22--"(Θ<sub>2</sub><sup>(2)</sup>)<sub>1</sub>"-->z23
a22--"(Θ<sub>2</sub><sup>(2)</sup>)<sub>2</sub>"-->z13
z12--g-->a12
z22--g-->a22
z13--g-->a13
z23--g-->a23
a13-.->y1-.->j
a23-.->y2-.->j
subgraph x
x1((x<sub>1</sub>))
x2((x<sub>2</sub>))
end
subgraph 第一层
direction LR
z12(("z<sub>1</sub><sup>(2)</sup>"))
a12(("a<sub>1</sub><sup>(2)</sup>"))
z22(("z<sub>2</sub><sup>(2)</sup>"))
a22(("a<sub>2</sub><sup>(2)</sup>"))
end
subgraph 第二层
z13(("z<sub>1</sub><sup>(3)</sup>"))
a13(("a<sub>1</sub><sup>(3)</sup>"))
z23(("z<sub>2</sub><sup>(3)</sup>"))
a23(("a<sub>2</sub><sup>(3)</sup>"))
end
subgraph y
y1((ŷ<sub>1</sub>))
y2((ŷ<sub>2</sub>))
end
j(("J(θ)"))
如图(省略了偏置),输入数据为 \(\boldsymbol x=\begin{bmatrix}x_1\\x_2\end{bmatrix}\) ,实际输出为 \(\boldsymbol y=\begin{bmatrix}y_1\\y_2\end{bmatrix}\)
这张图上表示了所有的运算,例如:
\[a_1^{\left(2\right)}=g\left(z_1^{\left(2\right)}\right)
\]
\[z_2^{\left(2\right)}=\left(\Theta_1^{\left(1\right)}\right)_2x_1+\left(\Theta_2^{\left(1\right)}\right)_2x_2
\]
同时,此图认为预测输出为 \(\hat y_1=a_1^{\left(3\right)}\) ,即有误差(注意此处不是定义而是结论):
\[\delta_1^{\left(3\right)}=\hat y_1-y_1=a_1^{\left(3\right)}-y_1
\]
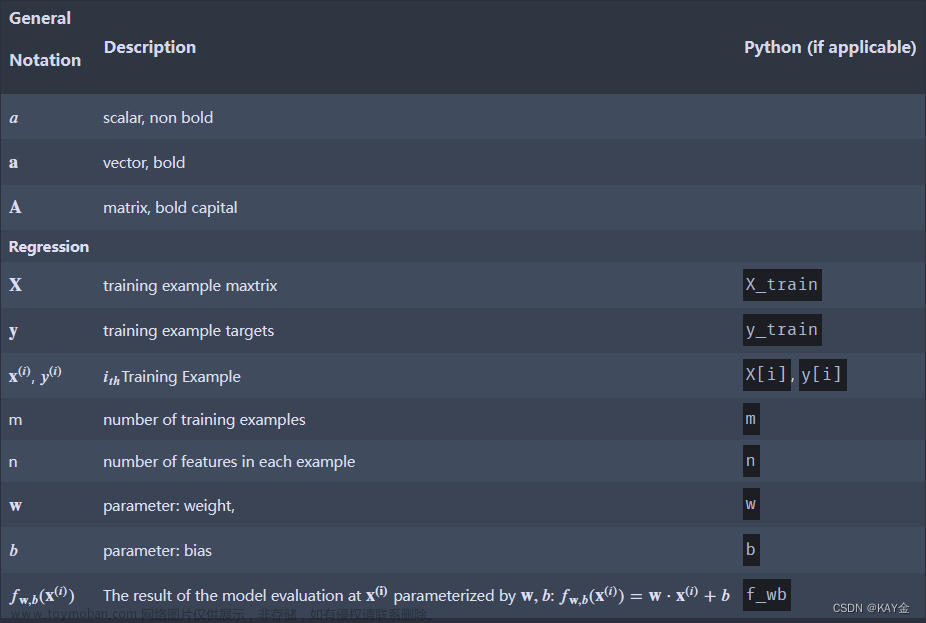
下面我们将上列函数改写成对应元素的写法,先作定义:
-
\(L\) :被 \(\Theta\) 作用的层
-
\(m\) : \(L\) 层单元数量,用 \(j\) 进行遍历(即 \(j\in\left\{1,2,\cdots,m\right\}\) )
-
\(n\) : \(L+1\) 层单元数量,用 \(i\) 进行遍历
推导
综上可得,若 \(L\) 是倒数第二层,则给出定义:
\[\begin{align*}\delta_i^{\left(L+1\right)}
&=\frac{\partial J}{\partial z_i^{\left(L+1\right)}}\\
&=\frac{\partial J}{\partial a_i^{\left(L+1\right)}}&&\cdot
\frac{\partial a_i^{\left(L+1\right)}}{\partial z_i^{\left(L+1\right)}}\\
&=\left(\frac{-y_i}{a_i^{\left(L+1\right)}}+\frac{1-y_i}{1-a_i^{\left(L+1\right)}}\right)&&\cdot
g^\prime z_i^{\left(L+1\right)}\\
&=\left(\frac{-y_i}{a_i^{\left(L+1\right)}}+\frac{1-y_i}{1-a_i^{\left(L+1\right)}}\right)&&\cdot
a_i^{\left(L+1\right)}\left(1-a_i^{\left(L+1\right)}\right)\\
&=a_i^{\left(L+1\right)}-y_i
\end{align*}\]
将同一层 \(\delta_i^{\left(L+1\right)}\) 合并为矩阵得( \(\boldsymbol\delta,\boldsymbol a,\boldsymbol y\) 都是列向量):
\[\boldsymbol\delta^{\left(L+1\right)}=\boldsymbol a^{\left(L+1\right)}-\boldsymbol y
\]
下面推隐含层,以第一个单元为例:
\[\begin{align*}
\delta_1^{\left(2\right)}&=\frac{\partial J}{\partial z_1^{\left(2\right)}}\\
&=\frac{\partial J}{\partial z_1^{\left(3\right)}}&&
\cdot\frac{\partial z_1^{\left(3\right)}}{\partial a_1^{\left(2\right)}}&&
\cdot\frac{\partial a_1^{\left(2\right)}}{\partial z_1^{\left(2\right)}}&&+
\frac{\partial J}{\partial z_2^{\left(3\right)}}&&
\cdot\frac{\partial z_2^{\left(3\right)}}{\partial a_1^{\left(2\right)}}&&
\cdot\frac{\partial a_1^{\left(2\right)}}{\partial z_1^{\left(2\right)}}\\
&=\delta_1^{\left(3\right)}&&
\cdot\left(\Theta_1^{\left(2\right)}\right)_1&&
\cdot g^\prime z_1^{\left(2\right)}&&+
\delta_2^{\left(3\right)}&&
\cdot\left(\Theta_1^{\left(2\right)}\right)_2&&
\cdot g^\prime z_1^{\left(2\right)}
\end{align*}\]
令:
\[\left\{\begin{align*}
\boldsymbol\delta^{\left(L\right)}&=\begin{bmatrix}\delta_1^{\left(L\right)}\\\delta_2^{\left(L\right)}\\\vdots\\\delta_n^{\left(L\right)}\end{bmatrix}\\
\boldsymbol\Theta_i^{\left(L\right)}&=\begin{bmatrix}
\left(\Theta_i^{\left(L\right)}\right)_1&
\left(\Theta_i^{\left(L\right)}\right)_2&
\cdots&
\left(\Theta_i^{\left(L\right)}\right)_n
\end{bmatrix}\end{align*}\right.\]
可将上式化为矩阵:
\[\delta_1^{\left(2\right)}
=\boldsymbol\Theta_1^{\left(2\right)}\boldsymbol\delta^{\left(3\right)}
\cdot g^\prime z_1^{\left(2\right)}\]
结论
由上,可写出递推普式:
\[\delta_j^{\left(L\right)}
=\boldsymbol\Theta_j^{\left(L\right)}\boldsymbol\delta^{\left(L+1\right)}\cdot g^\prime z_j^{\left(L\right)}\]
其中最后一层:文章来源:https://www.toymoban.com/news/detail-788582.html
\[\boldsymbol\delta^{\left(Last\right)}=\boldsymbol a^{\left(Last\right)}-\boldsymbol y
\]
到了这里,关于关于吴恩达机器学习中反向传播的理解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处: 如若内容造成侵权/违法违规/事实不符,请点击违法举报进行投诉反馈,一经查实,立即删除!