Leetcode 416 分割等和子集-Toy模板网

这篇具有很好参考价值的文章主要介绍了Leetcode 416 分割等和子集。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

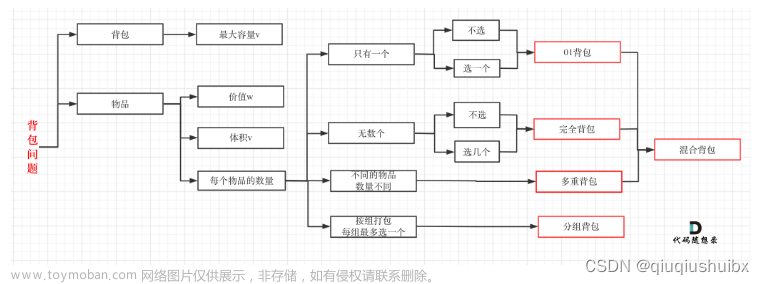
题意理解：

给你一个 只包含正整数 的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

即将数组的元素分成两组，每组数值=sum(nums)/2

若能分成这样的两组，则返回true,否则返回false

本质上，可以将这道题抽象为0-1背包问题，其中nums中的元素是物品，价值=元素大小，重量=元素大小。背包大小m=sum(nums)/2。

问题就转换成，将nums中的物品任取，放入大小为m的背包，如果此时背包的最大价值也是m，则返回true, 否则返回false。

解题思路：

首先理解题意，将其转换为一个背包问题，使用动态规划的思路来求解。

动态规划五部曲：

（1）dp[i][j]或dp[i]的含义

（2）递推公式：

dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+values[i])或

dp[j]=max(dp[j],dp[j-weight[i]]+values[i])

（3）根据题意初始化

（4）遍历求解:先遍历包还是先遍历物品

（5）打印——debug

1.动态规划二维dp数组

dp[i][j]表示下标[0,j]的元素任务，放入大小为j的背包，能获得的最大价值
递推公式：dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+values[i])
初始化第一行，第一列。
遍历：由于二维数组完整保留了两个维度所有信息，所以先遍历背包还是先遍历物品，都是可以的。

 public boolean canPartition(int[] nums) {
        int sum = 0;
        for(int i=0;i< nums.length;i++) sum+=nums[i];
        //不能分为两个相等的正整数
        if(sum%2!=0) return false;
        int target=(int)sum/2;
        int[][] dp=new int[nums.length][target+1];
        for(int i=0;i< nums.length;i++) Arrays.fill(dp[i],-1);
        for(int i=0;i< nums.length;i++) dp[i][0]=0;
        for(int j=0;j<=target;j++){
            if(nums[0]<=j) dp[0][j]=nums[0];
            else dp[0][j]=0;
        }
        for(int i=1;i<nums.length;i++){
            for(int j=1;j<=target;j++){
                if(nums[i]>j){
                    dp[i][j]=dp[i-1][j];
                }else{
                    dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-nums[i]]+nums[i]);
                }
            }
        }
        return dp[nums.length-1][target]==target?true:false;
    }

Leetcode 416 分割等和子集,刷题训练营,leetcode,算法,动态规划,数据结构

2.一维滚动数组——存储压缩

dp[j]表示装满大小为j的背包所能获得的最大价值。
递推公式：dp[j]=max(dp[j],dp[j-weight[i]]+values[i])
初始化：右边的值总是由最左边的值推导而来，而最坐标的值dp[0]表示背包大小为0所能获得的最大价值，所以有dp[0]=0.将所有元素初始化为0
遍历：由于以为滚动数组是二维dp数组的动态行滚动更新，所以遍历顺序总是先物品后背包。
注意：为了防止用同层修改过的值修改本行其他值，导致物体重复放置，故采用倒序遍历背包。

public boolean canPartition2(int[] nums) {
        int sum = 0;
        for(int i=0;i< nums.length;i++) sum+=nums[i];
        //不能分为两个相等的正整数
        if(sum%2!=0) return false;
        int target=(int)sum/2;
        int[] dp=new int[target+1];
        Arrays.fill(dp,0);
        for(int i=1;i<nums.length;i++){
            for(int j=target;j>=0;j--){
                if(nums[i]>j){
                    dp[j]=dp[j];
                }else{
                    dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
                }
            }
        }
        return dp[target]==target?true:false;
    }

Leetcode 416 分割等和子集,刷题训练营,leetcode,算法,动态规划,数据结构

3.分析

时间复杂度：O(n*target)

空间复杂度：

二维：O(n*target)

一维：O(target)

n是nums的长度，target是sum(nums)/2的大小文章来源地址https://www.toymoban.com/news/detail-788589.html

到了这里，关于Leetcode 416 分割等和子集的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！