prim和kruskal算法的正确性证明（贪心、最优子结构）-Toy模板网

这篇具有很好参考价值的文章主要介绍了prim和kruskal算法的正确性证明（贪心、最优子结构）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

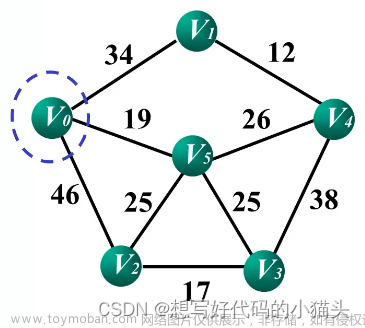
prim算法

贪心选择：

不失一般性，令起始节点为a，与a相连且度最小的另一节点为b，该边记作y，现证明y包括在某最优解中。令G为一颗最小生成树，

若其中包括y，算法正确性得证成立；若不包括y，则将y加入到G中，此时形成环，不考虑环以外节点，删除与a相邻另一条边c，删除后得新生成树G’,而，所以G'也一定为一颗最小生成树，算法正确性得证。

最优子结构：

不失一般性，设由prim算法得到的最小生成树为G，其中度最小的2个相邻节点为a,b，要证明最优子结构，此时需合并a,b为一个整体节点c,并删除连接a,b的边y，此时得到的新生成树记作G'，若G'是最小生成树，原问题正确性得证；若G'不是最小生成树，则存在另一最小生成树G''，且，将G''的c节点重新扩展为a,b得到最小生成树G''',此时

$克鲁斯卡尔最优子结构证明,算法,数据结构,动态规划$

但G是最小生成树，所以该公式矛盾，依次类推得证prim算法正确性。

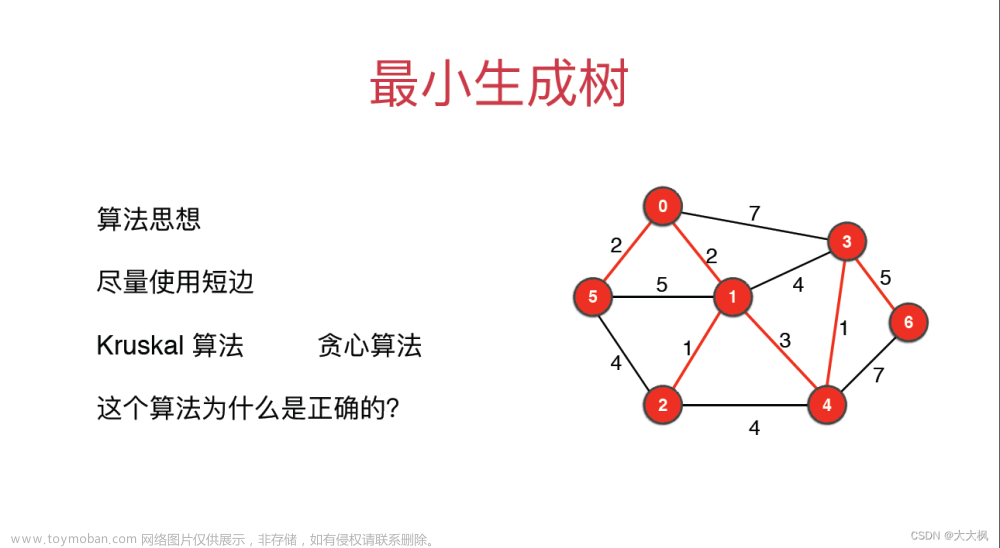
kruskal算法

贪心选择：

不失一般性，设Kruskal算法得到的树是G，假设令T为一颗最小生成树，若G=T原问题正确性已得证；若，G中至少有一条最小权值边在G中而不在T中，设该边为e,把e加入T中，此时形成环，再删掉环中不在G中的边f，得到新树T'，若w(f) > w(e), 则T’的权值和小于T的权值和，与T是最小生成树矛盾；若w(f) < w(e), 说明Kruskal算法在考虑加入e之前先考虑了边f，之所以没加入f是因为f和之前加入的边形成环，之前加入的边权值显然不超过w(f) (因为加边是从小到大的顺序加入的)，所以之前加入的边权值一定小于w(e)。而根据e的定义，G中权值小于w(e)的边都在T中，这说明T中的边会和f构成环，矛盾。所以只能w(f) = w(e)，T’仍然是最小生成树，而T’和G相同的边多了一条。原问题正确性得证。

最优子结构：

不失一般性，设由Kruskal算法得到的最小生成树为G，其中权值最小的边为e，要证明最优子结构，此时需合并以e为边的两个节点a,b为一个整体节点c,并删除边e，此时得到的新生成树记作G'，若G'是最小生成树，原问题正确性得证；若G'不是最小生成树，则存在另一最小生成树G''，且，将G''的c节点重新扩展为以e为边的两个节点a,b得到最小生成树G''',此时

$克鲁斯卡尔最优子结构证明,算法,数据结构,动态规划$