P1164-小A买菜（动态规划，01背包）-Toy模板网

这篇具有很好参考价值的文章主要介绍了P1164-小A买菜（动态规划，01背包）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

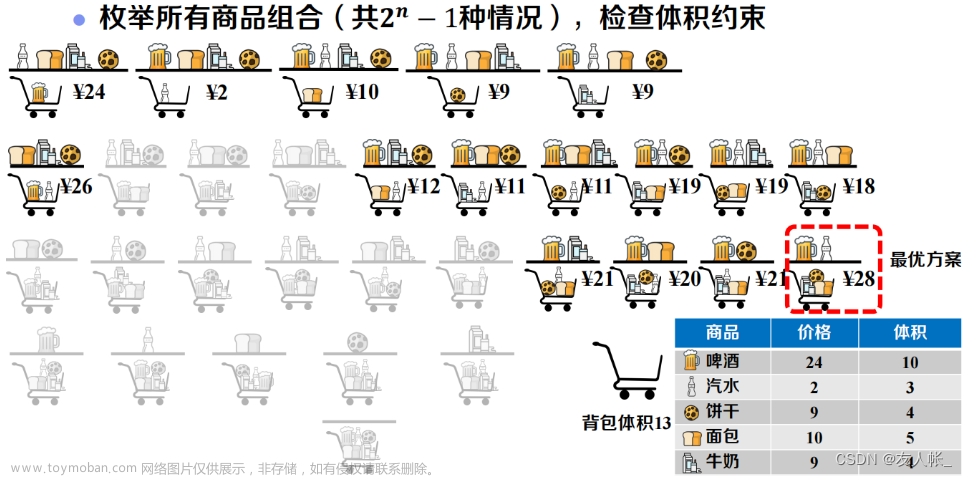
动态规划

#include<iostream>
using namespace std;
const long long N = 1e5 + 9;
int dp[1000][1000];
int a[N];
int main() {
	long long m, n,ans=0;
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 0; i <= n; i++) {
		dp[i][0] = 1;
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			if (j >= a[i]) {
				dp[i][j] += dp[i - 1][j - a[i]];
			}
			dp[i][j] += dp[i - 1][j];
		}
	}
	cout << dp[n][m];
	return 0;
}

$l in e : 11$ 为所有花费 0 元的商品的方法赋值为 1; 因为花费0元的方法,有且仅有一种,那就是都不买

$l in e : 13 - 14$ 两次循环,外循环为商品的数目,内循环为花费的钱 ,即表示每 $i:(1\to n)$ 件商品花费 $\to m)$ 元的方法数, 先历遍商品数.(动态规划的方程为$ dp[i][j] += dp[i - 1][j - a[i]]$ 就是通过 $i - 1$ 的数目推出 $i$ 的数目,所以先历遍商品数)

if (j >= a[i]) {                     
	dp[i][j] += dp[i - 1][j - a[i]];
}
dp[i][j] += dp[i - 1][j];

其中 $d p [i] [j]$ 表示前 $i$ 个商品花费 $ j $ 元的方法数.

$d p [i] [j]$ 一共有两种情况:

买第 $i$ 件商品 : $d p [i] [j] + = d p [i - 1] [j - a [i]]$ 相当于在前 $i - 1$ 件商品花费 $j - a [i]$ 元的基础之上卖下了花费 $a [i]$ 元的 $i$ 这件商品(前提是 $j >= a [i]$ 可以买)
不买第 $i$ 件商品:$dp[i][j] += dp[i - 1][j] $ 那么就表示前 $i$ 件商品和前 $i - 1$ 件商品一样花费了 $j$ 元

因为求的是方法,所以两种情况都要加上, 其中不买 $i$ 这件商品这种情况一定存在

最后输出 $d p [n] [m]$ ,即一共 $n$ 件商品花费 m元的方法

优化为一维数组

为何可以优化？：

每次循环只用到了 $i$ 的上一个 $i - 1$

所以由 $d p [i] [j]$ 可以变为 $d p [j]$

#include<iostream>
using namespace std;
const long long N = 1e5 + 9;
int dp[N];
int a[N];
int main() {
	long long m, n, ans = 0;
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> a[i];
		dp[0]= 1;//表示最初始的那个，第一个商品花费0元的方法为1；
	for (int i = 1; i <= n; i++) {
		for (int j = m; j >= 1; j--) {//注意这里要反过来应为dp[j-a[i]]可能已经改变了
         	//这里省略了一步就是 dp[j]=dp[j] 这表示 不买的情况,下一个和上一个的方法数是一样的
			if (j >= a[i]) {
				dp[j] += dp[j - a[i]];//逐渐迭代
			}
		}
	}
	cout << dp[m];
	return 0;
}

$l in e : 15$ 一维的 $d p [j] + = d p [j - a [i]]$ 对比二维的 $d p [i] [j] + = d p [i - 1] [j - a [i]]$ 文章来源地址https://www.toymoban.com/news/detail-789097.html

$d p [j] + = d p [j - a [i]]$ , 表示花费 $j - a [i]$ 元可以卖下前 $i - 1$ 个商品的方法数的基础上买下 $i$ 这件商品的方法数,直接覆盖掉 $d p : i - 1$ 的
所以要倒过来历遍 $j:(m\to 1)$ ,以防 $d p [j - a [i]]$ 被覆盖了