前言:
这么长时间~~没有写了,尊都不是我懒嘛!
尊都一直在被考试折磨中啊

我也不知道为啥别人家的学校都是考试周而我们这个小小的科大是考试月!!!

看到周围学校都放假了,而我们却还有一个星期~

好了,话不多说啦~,开更~~~
平面图
先说定义:
在一个无向图G中,各边除了顶点相交外,其余各边均不相交,称这样的无向图G为可平面图
简称:平面图
注意:
1.(每个点度数不超过4的简单图都是平面图)
2.(非平面图的母图都是非平面图,平面图的子图都是平面图)
举个栗子:
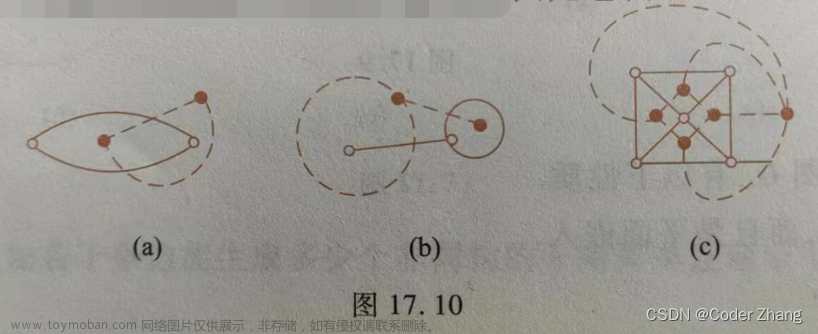
有些图从表面上看,它的某些边是相交的,但是不能就此肯定它不是平面图。
对于图(a)(b)中的无向图来说,加以重画之后,它将不包含任何边的交叉(e)(f)。(a)(b)是平面图,而(c)(d)是非平面图。

就是通俗一点吧,就是把里面的边可以挪动一下,看看能不能使原来的图变成除了顶点所连的边外,没有在相交的边(图中a和b经挪动变成了e,f,而e,f正好变成除了顶点所连的边外,没有在相交的边!
所以a,b是平面图,而c,d却不是(g是c挪的图,h是d挪的图)
面:给定平面图G的平面嵌入,G的边将平面划分成若干个区域,每个区域都称作G的一个面
其中有一个面的面积无限,称作“无限面或者外部面”
其余面的面积有限,称作“有限面或者内部面”
包围每个面的所有边组成的回路组称作该面的“边界”
边界的长度称作该面的边界
⭐面r的边数——>面的度,记D(r)
有限面=内部面 无限面=外部面

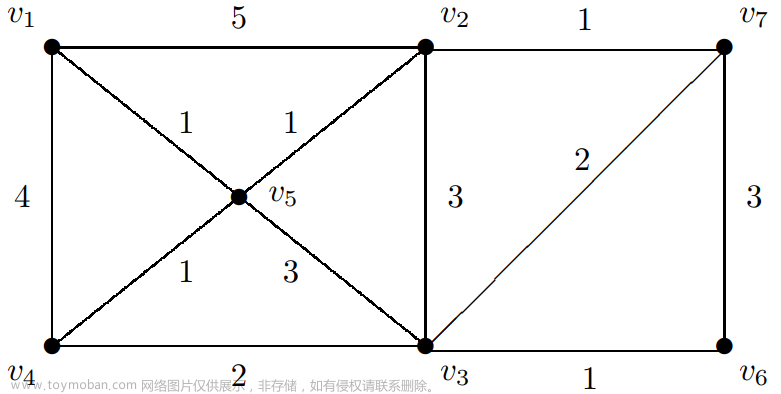
该图中就有4个面,构成的3个圈,外加一个外面!

由题可知R0的次数之和为R1+R2+R3+R4+外面
R1有7个边,次数为7
R2有环(代表两条边)+4条边,次数为6
所以R0为7+6=13
定理:平面图的所有面(有限面外加无限面)次数之和等于边数的二倍!
(说人话就是所有面的次数加和为边数的2倍,每个边会给两个面贡献次数)
极大平面图:
极大平面图是简单平面图,但是在任意两个不相邻的点之间加边就会变成非平面图特点:极大平面图一定连通 极大平面图不含有割点和桥
定理11.4:n 阶 连 通 简 单 平 面 图 是 极 大 平 面 图 ⇔ ∀ R , d e g ( R ) = 3
定理11.5:n ( n ≥ 4 ) 阶 极 大 平 面 图 G 中 , δ ( G ) ≥ 3
欧拉公式
欧拉公式:设G是连通平面图,则n − m + r = 2
其中r是G的面数,n是G的阶,m是G的边数
定理:设G是平面图,则n − m + r = 1 + p
其中r是G的面数,p是G的连通分支数
定理:设G是连通平面图,G的各面次数至少是L( ≥ 3 ) ,则m ≤ (n-2)L/(L-2)
定理:设平面图G有p个连通分支,G的各面次数至少是L( ≥ 3 ) ,则
M<=L(n-k-1)/(l-2);
定理:设n ( ≥ 3 ) 阶简单平面图G有m条边,则m =3n-6;
平面图的判断
平面图的判断:
插入2度顶点: 把 (u,v) 变成(u,w),(w,v)
删除2度顶点:deg(w)=2,把(u,w),(w,v)变成(u,v)
同胚:₁₂G₁,G₂同构或反复插入或删除2度顶点后同构
定理11.13:图G是平面图⇔G没有与₅K₅或K3,3同胚的子图
定理11.14: 图G是平面图⇔G没有可以边收缩到₅K₅或K₃,₃的子图
平面图的对偶图
对偶图的点数:n∗=x
对偶图的边数:m∗=m
对偶图的面数:r∗=n−p+1
对偶图的性质
1.如果G是连通的,则G*与G互为对偶图
2. G*是平面图,而且是平面嵌入
3. G*是连通的
4.若边e为G中的环,则G*与e对应的边e*为桥,若e为桥,则G*中与e对应的边e*为环
5.在多数情况下,G*是多重图
6.同构的平面图的对偶图不一定同构
自对偶图:
定理11.18: n≥4时,轮图ₙWₙ是自对偶图
小小离散!嘿嘿,还不拿捏你?
剩下的会尽量更新完哒!
离散更新完了,会更新一些计算机语言吼~~
大家一起进步~~~
最后的最后~,我想说的是这个排版正在努力学习哈(尬笑)
可能现在整的不是特别好,但是相信在不久的将来,一定会变得更加好看的~~文章来源:https://www.toymoban.com/news/detail-789662.html
如果哪里写错了,或者对于某个知识点有更好的理解,欢迎在评论区留言吼~文章来源地址https://www.toymoban.com/news/detail-789662.html
到了这里,关于离散数学(屈婉玲)图论<四>平面图的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!