PID横向控制和仿真实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了PID横向控制和仿真实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

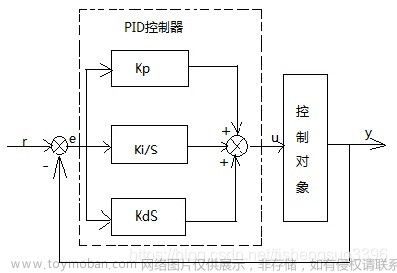
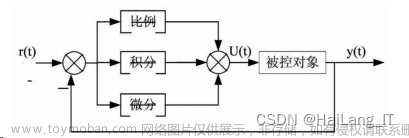
1. PID介绍

PID是一种常见的控制算法，全称为Proportional-Integral-Derivative，即比例-积分-微分控制器。PID控制器是一种线性控制器，它将设定值与实际值进行比较，根据误差的大小，控制器会相应地调整系统的比例、积分和微分系数，以减小误差。

PID控制器的基本公式为：

$K_p * e(t) + K_i * \int^{t}_{0}{e(\tau)} d\tau + K_d *\frac{d}{dt} e(t) \tag{1}$

其中，$u(t) $是控制器的输出，$ e(t)$ 是误差信号（设定值与实际值之差）， $K_p$ 、 $K_i$ 和 $K_d$ 是控制器的比例、积分和微分系数。

PID控制器在工程、科学和工业等领域中有着广泛的应用。例如，在汽车定速巡航系统、空调系统、工业自动化生产线等系统中都可以看到PID控制器的身影。此外，PID控制器还广泛应用于机器人控制、化工生产、航天器控制等领域。

将公式(1)转换为离散形式，则有

$K_p * e(n) + K_i * T*\sum^{n}_{i=0}{e(i)} + K_d *\frac{e(n)-e(n-1)}{T} \tag{2}$

其中 $T$ 为采样周期，由此公式可以得到PID代码的实现如下

#PID.py

class PIDController:
    def __init__(self, Kp, Ki, Kd):
        self.Kp = Kp
        self.Ki = Ki
        self.Kd = Kd
        self.previous_error = 0
        self.integral = 0


    def cal_output(self, error, dt):
        derivative = error - self.previous_error
        u = self.Kp * error + self.Ki * self.integral * dt + self.Kd * derivative / dt
        self.integral += error
        self.previous_error = error
        return u

2. PID横向控制原理

在自动驾驶横向控制中，主要通过控制方向盘的角度来控制车辆的横向距离误差，因此我们可以通过横向距离误差 $e_y$ 来作为PID的输入，输出可以作为方向盘转角 $\delta_f$ ，结合之前我们的车辆运动学模型（这里我们假设方向盘转角与前轮转角比是1），横向误差计算的几何结构如下图所示：

PID横向控制和仿真实现,自动驾驶-控制,pid,自动驾驶-控制,控制,汽车

图中

$P$ ：当前车辆的目标点车
$l_d$ ：车辆后轴中心点 $A$ 到 $F$ 的距离
$\theta$ ： $l_d$ 与车轴的夹角
$\varphi$ ：车辆的航向角
$e_y$ ：横向偏差

由 $A$ 和 $P$ 的坐标可以计算得

$\beta = arctan\frac{y_1-y_0}{x_1-x_0} \tag{3}$

由图中的几何关系，我们可以得到

$e_y = l_d sin\theta =l_d sin(\beta - \varphi)\tag{4}$

其中 $\varphi$ 为车辆的航向角yaw，其实现方法详见bicycle_model.py

3. 算法和仿真实现

bicycle_model.py

#!/usr/bin/python
# -*- coding: UTF-8 -*-

import math
import matplotlib.pyplot as plt
import numpy as np
from celluloid import Camera


class Vehicle:
    def __init__(self,
                 x=0.0,
                 y=0.0,
                 yaw=0.0,
                 v=0.0,
                 dt=0.1,
                 l=3.0):
        self.steer = 0
        self.x = x
        self.y = y
        self.yaw = yaw
        self.v = v
        self.dt = dt
        self.L = l  # 轴距
        self.x_front = x + l * math.cos(yaw)
        self.y_front = y + l * math.sin(yaw)

    def update(self, a, delta, max_steer=np.pi):
        delta = np.clip(delta, -max_steer, max_steer)
        self.steer = delta

        self.x = self.x + self.v * math.cos(self.yaw) * self.dt
        self.y = self.y + self.v * math.sin(self.yaw) * self.dt
        self.yaw = self.yaw + self.v / self.L * math.tan(delta) * self.dt

        self.v = self.v + a * self.dt
        self.x_front = self.x + self.L * math.cos(self.yaw)
        self.y_front = self.y + self.L * math.sin(self.yaw)


class VehicleInfo:
    # Vehicle parameter
    L = 3.0  #轴距
    W = 2.0  #宽度
    LF = 3.8  #后轴中心到车头距离
    LB = 0.8  #后轴中心到车尾距离
    MAX_STEER = 0.6  # 最大前轮转角
    TR = 0.5  # 轮子半径
    TW = 0.5  # 轮子宽度
    WD = W  #轮距
    LENGTH = LB + LF  # 车辆长度

def draw_trailer(x, y, yaw, steer, ax, vehicle_info=VehicleInfo, color='black'):
    vehicle_outline = np.array(
        [[-vehicle_info.LB, vehicle_info.LF, vehicle_info.LF, -vehicle_info.LB, -vehicle_info.LB],
         [vehicle_info.W / 2, vehicle_info.W / 2, -vehicle_info.W / 2, -vehicle_info.W / 2, vehicle_info.W / 2]])

    wheel = np.array([[-vehicle_info.TR, vehicle_info.TR, vehicle_info.TR, -vehicle_info.TR, -vehicle_info.TR],
                      [vehicle_info.TW / 2, vehicle_info.TW / 2, -vehicle_info.TW / 2, -vehicle_info.TW / 2, vehicle_info.TW / 2]])

    rr_wheel = wheel.copy() #右后轮
    rl_wheel = wheel.copy() #左后轮
    fr_wheel = wheel.copy() #右前轮
    fl_wheel = wheel.copy() #左前轮
    rr_wheel[1,:] += vehicle_info.WD/2
    rl_wheel[1,:] -= vehicle_info.WD/2

    #方向盘旋转
    rot1 = np.array([[np.cos(steer), -np.sin(steer)],
                     [np.sin(steer), np.cos(steer)]])
    #yaw旋转矩阵
    rot2 = np.array([[np.cos(yaw), -np.sin(yaw)],
                     [np.sin(yaw), np.cos(yaw)]])
    fr_wheel = np.dot(rot1, fr_wheel)
    fl_wheel = np.dot(rot1, fl_wheel)
    fr_wheel += np.array([[vehicle_info.L], [-vehicle_info.WD / 2]])
    fl_wheel += np.array([[vehicle_info.L], [vehicle_info.WD / 2]])

    fr_wheel = np.dot(rot2, fr_wheel)
    fr_wheel[0, :] += x
    fr_wheel[1, :] += y
    fl_wheel = np.dot(rot2, fl_wheel)
    fl_wheel[0, :] += x
    fl_wheel[1, :] += y
    rr_wheel = np.dot(rot2, rr_wheel)
    rr_wheel[0, :] += x
    rr_wheel[1, :] += y
    rl_wheel = np.dot(rot2, rl_wheel)
    rl_wheel[0, :] += x
    rl_wheel[1, :] += y
    vehicle_outline = np.dot(rot2, vehicle_outline)
    vehicle_outline[0, :] += x
    vehicle_outline[1, :] += y

    ax.plot(fr_wheel[0, :], fr_wheel[1, :], color)
    ax.plot(rr_wheel[0, :], rr_wheel[1, :], color)
    ax.plot(fl_wheel[0, :], fl_wheel[1, :], color)
    ax.plot(rl_wheel[0, :], rl_wheel[1, :], color)

    ax.plot(vehicle_outline[0, :], vehicle_outline[1, :], color)
    # ax.axis('equal')



if __name__ == "__main__":

    vehicle = Vehicle(x=0.0,
                      y=0.0,
                      yaw=0,
                      v=0.0,
                      dt=0.1,
                      l=VehicleInfo.L)
    vehicle.v = 1
    trajectory_x = []
    trajectory_y = []
    fig = plt.figure()
    # 保存动图用
    # camera = Camera(fig)
    for i in range(600):
        plt.cla()
        plt.gca().set_aspect('equal', adjustable='box')
        vehicle.update(0, np.pi / 10)
        draw_trailer(vehicle.x, vehicle.y, vehicle.yaw, vehicle.steer, plt)
        trajectory_x.append(vehicle.x)
        trajectory_y.append(vehicle.y)
        plt.plot(trajectory_x, trajectory_y, 'blue')
        plt.xlim(-12, 12)
        plt.ylim(-2.5, 21)
        plt.pause(0.001)
    #     camera.snap()
    # animation = camera.animate(interval=5)
    # animation.save('trajectory.gif')

main.py

from scipy.spatial import KDTree
from bicycle_model import Vehicle, VehicleInfo, draw_trailer
from PID import PIDController
import numpy as np
import matplotlib.pyplot as plt
import math
import imageio

MAX_SIMULATION_TIME = 200.0  # 程序最大运行时间200*dt
PID = PIDController(2, 0.001, 3)


def NormalizeAngle(angle):
    a = math.fmod(angle + np.pi, 2 * np.pi)
    if a < 0.0:
        a += (2.0 * np.pi)
    return a - np.pi


def main():
    # 设置跟踪轨迹
    ref_path = np.zeros((1000, 2))
    ref_path[:, 0] = np.linspace(0, 50, 1000)  # x坐标
    ref_path[:, 1] = 10 * np.sin(ref_path[:, 0] / 20.0)  # y坐标
    ref_tree = KDTree(ref_path)
    # 假设车辆初始位置为（0，0），航向角yaw=0.0，速度为2m/s，时间周期dt为0.1秒
    vehicle = Vehicle(x=0.0,
                      y=0.0,
                      yaw=np.pi/2,
                      v=2.0,
                      dt=0.1,
                      l=VehicleInfo.L)

    time = 0.0  # 初始时间

    # 记录车辆轨迹
    trajectory_x = []
    trajectory_y = []
    lat_err = []  # 记录横向误差

    i = 0
    image_list = []  # 存储图片
    plt.figure(1)

    last_idx = ref_path.shape[0] - 1  # 跟踪轨迹的最后一个点的索引
    old_idx = 0  # 记录上一次的索引点
    target_ind = 0  # 第一个目标点的索引
    while MAX_SIMULATION_TIME >= time and last_idx > target_ind:
        time += vehicle.dt  # 累加一次时间周期
        vehicle_positon = np.zeros(2)
        vehicle_positon[0] = vehicle.x
        vehicle_positon[1] = vehicle.y
        distance, target_ind = ref_tree.query(vehicle_positon)  # 在跟踪轨迹上查找离车辆最近的点
        if old_idx > target_ind:
            print("ERROR: Find the point behind the vehicle.")
            target_ind = old_idx + 1  # 查找到车辆后面的点，将目标点索引置为上一次的索引点idx+1
        old_idx = target_ind  # 记录本次索引点idx
        alpha = math.atan2(
            ref_path[target_ind, 1] - vehicle_positon[1], ref_path[target_ind, 0] - vehicle_positon[0])
        l_d = np.linalg.norm(ref_path[target_ind] - vehicle_positon)  # 目标点与车定位点距离l_d

        theta_e = NormalizeAngle(alpha - vehicle.yaw)
        e_y = l_d * math.sin(theta_e)  # 计算实际误差，0为目标距离
        lat_err.append(e_y)
        delta_f = PID.cal_output(e_y, vehicle.dt)

        vehicle.update(0.0, delta_f, np.pi / 10)  # 由于假设纵向匀速运动，所以加速度a=0.0
        trajectory_x.append(vehicle.x)
        trajectory_y.append(vehicle.y)

        # 显示动图
        plt.cla()
        plt.plot(ref_path[:, 0], ref_path[:, 1], '-.b', linewidth=1.0)
        draw_trailer(vehicle.x, vehicle.y, vehicle.yaw, vehicle.steer, plt)

        plt.plot(trajectory_x, trajectory_y, "-r", label="trajectory")
        plt.plot(ref_path[target_ind, 0], ref_path[target_ind, 1], "go", label="target")
        plt.axis("equal")
        plt.grid(True)
        plt.pause(0.001)
        plt.savefig("temp.png")
        i += 1
        if (i % 50) > 0:
            image_list.append(imageio.imread("temp.png"))

    imageio.mimsave("display.gif", image_list, duration=0.1)

    plt.figure(2)
    plt.subplot(2, 1, 1)
    plt.plot(ref_path[:, 0], ref_path[:, 1], '-.b', linewidth=1.0)
    plt.plot(trajectory_x, trajectory_y, 'r')
    plt.title("actual tracking effect")

    plt.subplot(2, 1, 2)
    plt.plot(lat_err)
    plt.title("lateral error")
    plt.show()


if __name__ == '__main__':
    main()