机器人传感器及其信息融合技术-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器人传感器及其信息融合技术。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

机器人传感器及其信息融合技术

第一章传感器的基础知识

第五章多传感器信息融合技术概述

信息融合三个核心特征：

信息融合是在多个层次上完成对多源信息处理的过程，其中每一个层次都表示不同级别的信息抽象。
信息融合包括探测、互联、相关、估计以及信息组合。
信息融合的结果包括较低层次上的状态估计，以及较高层次上的整个系统的状态估计。

多传感器信息融合的分类

按信息传递方式分类

串联型信息融合
并联型信息融合
串并混合型信息融合

按处理对象层次不同分类

像素级融合
特征层融合
决策层融合

多传感器融合方法

多传感器融合算法分类

第六章多传感器的定量信息融合

传感器建模

建立传感器模型考虑的原则：

传感器模型必须能反映观察中的不确定性。
传感器模型必须能方便地在同一参照系内表达。
传感器模型中必须包扩一系列环境特征向量及有关这些特征的先验知识。

基于参数估计的信息融合方法

假设在给定时刻，待测系统的状态向量是 $X$ ,传感器测量值是 $Y$ ，则该传感器的测量模型为

$Y = f (X) + V$

其中 $V$ 是符合高斯分布的噪声项。所谓的数据融合就是：由 $N$ 个传感器得到测量值 $Y_1$ 、 $Y_2$ 、… 、 $Y_N$ ，并按照某种估计准则从这些测量值中得到特征参数 $X$ 的最优估计。
首先使用仅由一个传感器的测量值 $Y$ ，来估计状态 $X$ 的问题。
记状态 $X$ 的估计值为 $\hat{X}(Y)$ ，并定义 $L[\hat{X}(Y), X]$ 为损失函数，相应的风险表达式为

$L[\hat{X}(Y), X]=\int \mathrm{d} Y p(x) \int \mathrm{d} X p(x \mid y) L[\hat{X}(Y), X]\tag{4}$

损失函数（loss function）用来预测模型单次预测的好坏，即模型的预测值 $f (X)$ 和真实值 $Y$ 之间的差别，记作 $L (Y, f (x))$ 。损失函数越小，表示模型预测越准确。

风险函数（risk function）又称期望损失(expected loss)，是损失函数的期望，度量平均意义下模型预测的好坏。机器学习的目标就是选择期望风险最小的模型。

其中 $p (x)$ 、 $\mid y)$ 表示概率分布。取风险最小的作为估计准则，使

$\left.\frac{\partial R}{\partial X}\right|_{X=\tilde{X}(Y)}=0$

即可取得状态的估计值 $\hat{X}(Y)$ 。对于不同的 $L[\hat{X}(Y), X]$ 得到不同的估计结果。常用的有：

$\begin{aligned}& L[\hat{X}(Y), X]=(X-\hat{X})^{\mathrm{T}} W(X-\hat{X}) \\& L[\hat{X}(Y), X]=\left[(X-\hat{X})^{\mathrm{T}} W(X-\hat{X})\right]^{1 / 2} \\& L[\hat{X}(Y), X]= \begin{cases}1 & |\hat{X}-X| \geqslant \frac{\varepsilon}{2} \\0 & |\hat{X}-X|<\frac{\varepsilon}{2}\end{cases} \\&\end{aligned}$

其中 $W$ 为正定权矩阵， $\varepsilon$ 为任意小的正数。相应的状态最优估计（最大后验估计）为

$\hat{X}_{\text {opt }}(Y)=\operatorname{argmax} p(X \mid Y)$

正定权矩阵通常指在数学和统计学中用于描述线性模型的一种矩阵。它通常被用于表示观测值之间的相关性或协方差。
在统计建模中，当我们对多个变量进行建模时，这些变量之间可能存在相关性。协方差矩阵是一种描述变量之间相关性的方法。如果这个协方差矩阵是正定的，那么它可以被称为正定权矩阵。

在具有 $N$ 个传感器的系统中，相应的信息融合可以看做是在观测值 $Y_1$ 、 $Y_2$ 、… 、 $Y_N$ 下，状态 $X$ 具有最大后验的估计，写作

$\hat{X}(Y)=\operatorname{argmax} p\left(X \mid Y_1, Y_2, \cdots, Y_N\right)$

第七章多传感器的定性信息融合

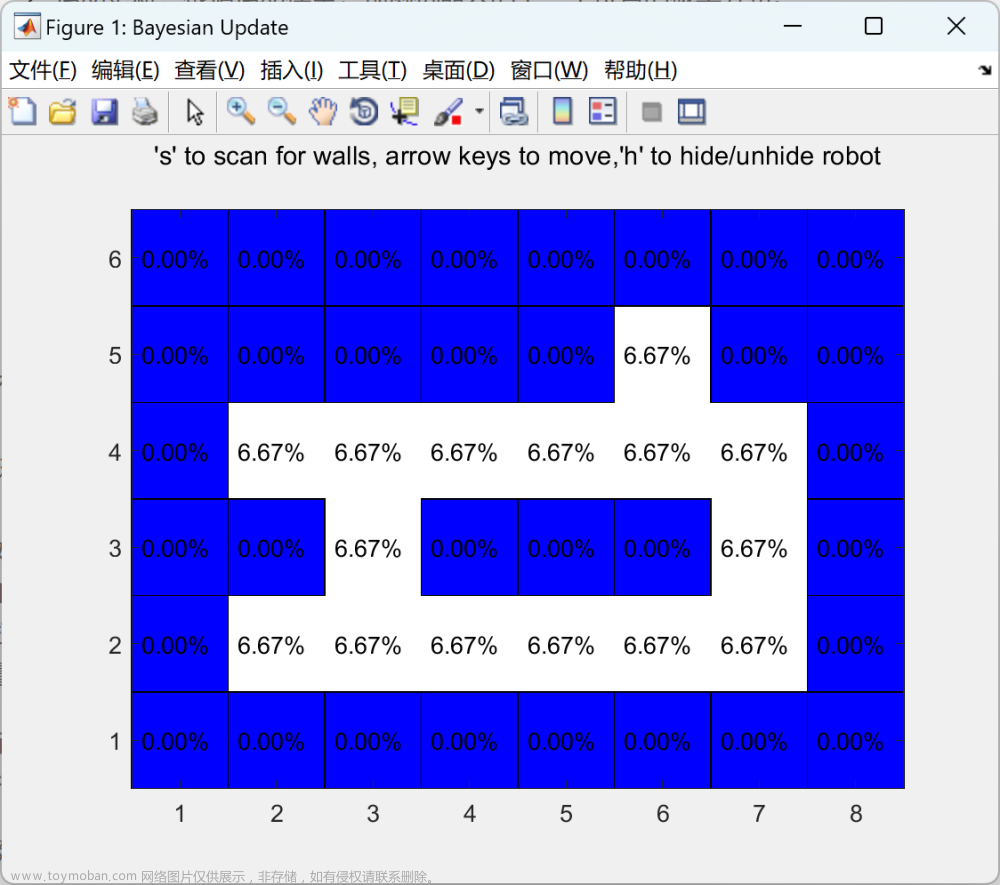
使用Bayes方法用于多传感器信息融合：在系统有m种可能决策的前提下，用Bayes方法判定哪种决策更具有可能性。

$P\left(A_i \mid B_1 \wedge B_2 \wedge \cdots \wedge B_n\right)=\frac{\prod_{k=1}^n P\left(B_k \mid A_i\right) P\left(A_i\right)}{\sum_{j=1}^m \prod_{k=1}^n P\left(B_k \mid A_j\right) P\left(A_j\right)} \quad(i=1, \cdots, n)$

其中 $A_i$ 表示各决策， $B_k$ 表示各个传感器的观测结果。如果能够利用系统的先验知识以及传感器的特性得到各先验概率 $P(A_i)$ ，以及条件概率 $P\left(B_k \mid A_i\right)$ ，就能判定哪种决策更具有可能性。

Bayes法多传感器信息融合

第十章多传感器信息融合在移动机器人中的应用

视觉与超声传感器的信息融合

自适应加权融合算法：不同传感器其加权因子各不相同，根据传感器的测量量，寻找均方误差最小的加权因子，从而以自适应方式求得最优融合解。总均方差 $\sigma^2$ 是关于各加权因子的多元二次函数

$\sigma^2=E\left|\left(x-\frac{\Lambda}{x}\right)^2\right|=\sum_{i=1}^n w_i^2 \sigma_i^2$

总均方误差最小时所对应的加权因子为
$w_i^*=\frac{1}{\sigma_i^2 \sum_{j=1}^n \frac{1}{\sigma_j^2}}(i=1,2, \cdots, n)$

则均方误差最小值为
$\sigma_{\min }^2=\frac{1}{\sum_{i=1}^n \frac{1}{\sigma_j^2}} \quad(i=1,2, \cdots, n)$

融合值可表示为
$\stackrel{\Lambda}{x}(k)=\sum_{i=1}^n \omega_i(k) x_i(k)$

其中 $\omega_i(k)$ 表示采样时刻 $k$ 时第 $i$ 个传感器的加权系数； $x_i(k)$ 表示采样时刻 $k$ 时第 $i$ 个传感器的测量值； $\stackrel{\Lambda}{x}(k)$ 则为采样时刻 $k$ 时传感器的加权融合结果。
因此，自适应加权融合算法的基本步骤为：* 计算方差 $\sigma_i^2$ ；
- 计算加权因子 $\omega_i(k)$ ；
- 计算融合值 $\stackrel{\Lambda}{x}(k)$ 。
方差的自适应求解方法：传感器的测量方差是一个随影响因素不断变化的量，因此需要根据传感器测量值计算出相应的 $\sigma_i^2$ 。
设存在两个不同传感器 $i$ 、 $j$ ，其测量值分别为 $x_i$ 、 $x_j$ ，观测误差分别为 $v_i$ 、 $v_j$ ，即 $x_i=x+v_i$ 、 $x_j=x+v_j$ ，则传感器 $i$ 、 $j$ 方差分别为：

$\sigma_i^2=E\left[v_i^2\right] ; \sigma_j^2=E\left[v_j^2\right]$

因为 $v_i$ 、 $v_j$ 互不相关，且均值为0，与 $x$ 也不相关，所以 $x_i$ 、 $x_j$ 的互协方差 $R_{i j}$ 为
$R_{i j}=E\left[x_i x_j\right]=E\left[x^2\right]$

$x_i$ 的自协方差 $R_{i i}$ 为
$R_{i i}=E\left[x_i x_i\right]=E\left[x^2\right]+E\left[v_i^2\right]$

设传感器测量数据个数为 $k$ ， $R_{i i}$ 估计值为 $R_{i i}(k)$ ， $R_{i j}$ 估计值为 $R_{i j}(k)$ ，则
$\begin{aligned}R_{i i}(k) & =\frac{1}{k} \sum_{i=1}^k x_i(l) x_i(l) \\& =\frac{k-1}{k} R_{i i}(k-1)+\frac{1}{k} x_i(k) x_i(k)\end{aligned}$

同理，
$R_{i j}(k)=\frac{k-1}{k} R_{i j}(k-1)+\frac{1}{k} x_i(k) x_j(k)$

如果传感器 $j$ 与传感器 $i$ 做相关运算，则可以得到 $R_{i j}(k)$ 的值。因此对于 $R_{i j}$ 可以进一步用 $R_{i j}(k)$ 的均值 $R_{i}(k)$ 来做它的估计，即：
$R_{i j}(k)=R_i(k)=\frac{1}{n-1} \sum_{j=1, j \neq i}^n R_{i j}(k)$

由此，可以估计出第 $k$ 时刻各个传感器的方差为：
$\sigma_i^2(k)=R_{i i}(k)-R_i(k)=R_{i i}(k)-\frac{1}{n-1} \sum_{j=1, j \neq i}^n R_{i j}(k)$

写成递推公式为： $\left\{\begin{array}{c}\sigma_i^2(k)=\frac{k-1}{k} \sigma_i^2(k-1)+\frac{1}{k} \sigma_i^2(k) \quad k=1,2 \cdots \\\sigma_i^2(0)=0\end{array}\right.$ 文章来源地址https://www.toymoban.com/news/detail-790344.html