机器学习 -决策树的案例-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器学习 -决策树的案例。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

场景

我们对决策树的基本概念和算法其实已经有过了解，那我们如何利用决策树解决问题呢？

构建决策树

数据准备

我们准备了一些数据如下：

# 定义新的数据集
new_dataSet = [
    ['晴朗', '是', '高', '是'],
    ['雨天', '否', '低', '否'],
    ['阴天', '是', '中', '是'],
    ['晴朗', '否', '高', '是'],
    ['晴朗', '是', '低', '否'],
    ['雨天', '是', '高', '否'],
    ['阴天', '否', '中', '是'],
    ['晴朗', '否', '低', '否']
]

这些数据分别是天气，是否闷热，风速和是否出门郊游。
现在要解决的问题是“基于当前的天气和其他条件，我们是否应该进行户外活动？

构建决策树

我们先检查这个数据集类别是否相同：

 classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]

很显然，数据集类别不同，那么我们需要检查是否还有特征可分:如果说，只有类别特征的话，我们选择多数：

 if len(dataSet[0]) == 1:
        return majorityCnt(classList)


def majorityCnt(classList):
    classCount = {}  # 创建一个空字典，用于存储每个元素及其出现次数
    # 遍历传入的列表
    for vote in classList:
        # 如果元素不在字典中，将其加入字典并初始化计数为0
        if vote not in classCount.keys():
            classCount[vote] = 0
        # 对于列表中的每个元素，增加其在字典中的计数
        classCount[vote] += 1

    # 对字典进行排序。这里使用sorted()函数，以字典的值（即元素的计数）作为排序依据。
    # key=operator.itemgetter(1)指定按照字典的值（第二个元素）来排序。
    # reverse=True表示降序排序，即出现次数最多的元素会排在最前面。
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)

    # 返回出现次数最多的元素。sortedClassCount[0]表示排序后的第一个元素（即出现次数最多的元素），
    # 而sortedClassCount[0][0]则是该元素本身。
    return sortedClassCount[0][0]

显然我们除了类别特征还有其他特征，我们选择最佳特征进行分割，所谓最佳特征，就是说有最高的信息增益的特征，信息增益的解释在上一节中有：
传送门：机器学习-决策树
最佳特征的索引是 2，对应于我们数据集中的 ‘风速’ 特征。这意味着在当前数据集中，'风速’在划分数据集时能提供最大的信息增益。OK

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1      # 计算特征的数量（减去最后一列标签）
    baseEntropy = calcShannonEnt(dataSet)  # 计算数据集当前的熵
    bestInfoGain = 0.0  # 初始化最佳信息增益
    bestFeature = -1    # 初始化最佳特征的索引
    for i in range(numFeatures):  # 遍历所有特征
        featList = [example[i] for example in dataSet]  # 提取当前特征列的所有值
        uniqueVals = set(featList)  # 获取当前特征的唯一值集合
        newEntropy = 0.0  # 初始化新熵
        for value in uniqueVals:  # 遍历当前特征的每个唯一值
            subDataSet = splitDataSet(dataSet, i, value)  # 根据当前特征和值分割数据集
            prob = len(subDataSet) / float(len(dataSet))  # 计算子数据集的比例
            newEntropy += prob * calcShannonEnt(subDataSet)  # 计算新熵，并累加

        infoGain = baseEntropy - newEntropy  # 计算信息增益
        if abs(infoGain) > abs(bestInfoGain):
            bestInfoGain = infoGain  # 更新最佳信息增益
            bestFeature = i  # 更新最佳特征索引
    return bestFeature  # 返回最佳特征的索引

下一步是使用这个特征来分割数据集，并递归地创建决策树。我们将对这个特征的每个唯一值进行分割，并在每个子集上重复此过程。这将形成决策树的不同分支。让我们开始构建决策树。

	bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]       #copy all of labels, so trees don't mess up existing labels
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)

如果一个特征有多个唯一值，那么 uniqueVals 将包含这些值，决策树的每个分支将对应这些值之一。
通过这些步骤，决策树逐渐在数据集的特征上进行分割，直到所有的数据都被正确分类或没有更多的特征可以用来进一步分割。

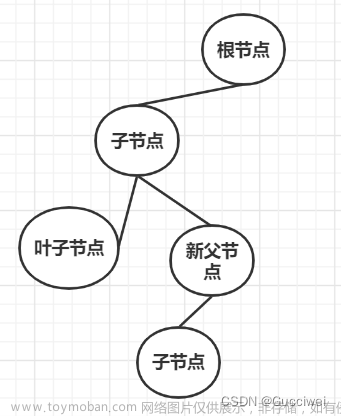
最终的决策树应该长这样：

{
    '其他条件2': {
        '低': '否', 
        '中': '是', 
        '高': {
            '天气': {
                '晴朗': '是', 
                '雨天': '否'
            }
        }
    }
}

完整可执行代码

完整的代码如下：


# 计算熵
def calcShannonEnt(dataSet):
    # 统计实例总数
    numEntries = len(dataSet)
    # 字典标签，统计标签出现的次数
    labelCounts = {}
    for data in dataSet:
        # 每个实例的最后一个元素是标签元素
        currentLabel = data[-1]
        if currentLabel not in labelCounts:
            labelCounts[currentLabel] = 0
            # 为当前类别标签的计数加一
        labelCounts[currentLabel] += 1

    # 设置初始熵
    shannonEnt = 0.0  # 初始化熵为0
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntries  # 计算每个类别标签的出现概率
        shannonEnt -= prob * log(prob, 2)  # 使用香农熵公式计算并累加熵
    return shannonEnt  # 返回计算得到的熵

def majorityCnt(classList):
    classCount = {}  # 创建一个空字典，用于存储每个元素及其出现次数

    # 遍历传入的列表
    for vote in classList:
        # 如果元素不在字典中，将其加入字典并初始化计数为0
        if vote not in classCount.keys():
            classCount[vote] = 0
        # 对于列表中的每个元素，增加其在字典中的计数
        classCount[vote] += 1

    # 对字典进行排序。这里使用sorted()函数，以字典的值（即元素的计数）作为排序依据。
    # key=operator.itemgetter(1)指定按照字典的值（第二个元素）来排序。
    # reverse=True表示降序排序，即出现次数最多的元素会排在最前面。
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)

    # 返回出现次数最多的元素。sortedClassCount[0]表示排序后的第一个元素（即出现次数最多的元素），
    # 而sortedClassCount[0][0]则是该元素本身。
    return sortedClassCount[0][0]


def splitDataSet(dataSet, axis, value):
    retDataSet = []  # 创建一个新的列表用于存放分割后的数据集
    for featVec in dataSet:  # 遍历数据集中的每个样本
        if featVec[axis] == value:  # 检查当前样本在指定特征轴上的值是否等于给定的值
            reducedFeatVec = featVec[:axis]  # 截取当前样本直到指定特征轴的部分
            reducedFeatVec.extend(featVec[axis+1:])  # 将指定特征轴之后的部分添加到截取的列表中
            retDataSet.append(reducedFeatVec)  # 将处理后的样本添加到分割后的数据集列表中
    return retDataSet  # 返回分割后的数据集

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1      # 计算特征的数量（减去最后一列标签）
    baseEntropy = calcShannonEnt(dataSet)  # 计算数据集当前的熵
    bestInfoGain = 0.0  # 初始化最佳信息增益
    bestFeature = -1    # 初始化最佳特征的索引

    for i in range(numFeatures):  # 遍历所有特征
        featList = [example[i] for example in dataSet]  # 提取当前特征列的所有值
        uniqueVals = set(featList)  # 获取当前特征的唯一值集合
        newEntropy = 0.0  # 初始化新熵
        for value in uniqueVals:  # 遍历当前特征的每个唯一值
            subDataSet = splitDataSet(dataSet, i, value)  # 根据当前特征和值分割数据集
            prob = len(subDataSet) / float(len(dataSet))  # 计算子数据集的比例
            newEntropy += prob * calcShannonEnt(subDataSet)  # 计算新熵，并累加

        infoGain = baseEntropy - newEntropy  # 计算信息增益
        if abs(infoGain) > abs(bestInfoGain):
            bestInfoGain = infoGain  # 更新最佳信息增益
            bestFeature = i  # 更新最佳特征索引

    return bestFeature  # 返回最佳特征的索引


def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]#stop splitting when all of the classes are equal
    if len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSet
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]       #copy all of labels, so trees don't mess up existing labels
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
    return myTree