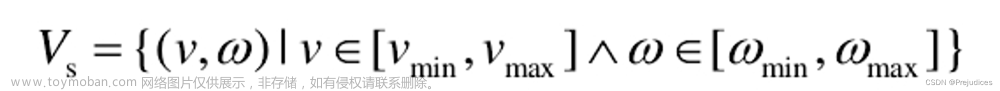Kriging代理模型理论相关推导

代理模型是指在分析和优化设计过程中可替代那些比较复杂和费时的数值分析的近似数学模型，也称为响应面模型、近似模型或元模型。代理模型方法可以大大提高优化设计效率、降低优化难度，并有利于实现并行优化设计。在现有代理模型方法中，源于地质统计学的Kriging模型是一种具有代表性的方法，本文对Kringing代理模型理论进行了一些推导。

1.1 代理模型问题的基本描述

对于一个有$m$个设计变量的优化问题，假定需要建立未知函数 $y:{\mathbb{R}}^m\to \mathbb{R}$ 对设计变量 $\mathbf{x}=[x_1{x}_2...x_m{]}^T\in {\mathbb{R}}^m$ 的代理模型。为此，首先采用试验设计方法在设计空间中进行抽样（如LHS方法或均匀采样方法），得到 $n$ 个样本点：
$$\mathbf{S}=[{\mathbf{x}}^{(1)}{\mathbf{x}}^{(2)}...{\mathbf{x}}^{(n)}]\in {\mathbb{R}}^{n\times m}\text{\hspace{1em}(1)}$$
对上述 $n$ 个样本点通过试验或者数值仿真得到其 $n$ 个响应值：
$${\mathbf{y}}_s=[y^{(1)}{y}^{(2)}...y^{(n)}{]}^T=[y({\mathbf{x}}^{(1)})y({\mathbf{x}}^{(2)})...y({\mathbf{x}}^{(n)}){]}^T\in {\mathbb{R}}^n\text{\hspace{1em}(2)}$$
所有样本点和对应的响应值构成样本数据集 $(\mathbf{S},{\mathbf{y}}_{\mathbf{s}})$，基于样本点数据集可以构建代理模型，这里主要介绍Kriging模型的建立方法。

说明：

如果一个样本对应多个响应值（目标函数），则需要对它们分别建立代理模型，或建立同时输出多个目标函数的代理模型。

1.2 Kriging模型及其预估值

Kriging模型是一种插值模型，其插值结果为已知样本响应值的线性加权，即：
$$\hat{y}(\mathbf{x})=\sum _{i=1}^n{\omega }^{(i)}{y}^{(i)}\text{\hspace{1em}(3)}$$
因此，只要给出加权系数$\mathbf{\omega }=[{\omega }^{(1)}{\omega }^{(2)}...{\omega }^{(n)}{]}^T$ 的值，就可以得到设计空间中任意点的响应值。为了计算加权系数，Kriging模型引入统计学假设：将未知函数看成是某个高斯静态随机过程的具体实现，该静态随机过程定义为：
$$Y(\mathbf{x})={\beta }_0+Z(\mathbf{x})\text{\hspace{1em}(4)}$$
上式中，${\beta }_0$ 为未知常数，也被称为全局趋势模型，代表 $Y(\mathbf{x})$的数学期望值；$Z(\cdot )$ 是均值为零、方差为 ${\sigma }^2$ 的静态随机过程。在设计空间不同位置处，这些随机变量存在一定的相关性（协方差），表示为：
$$Cov[Z(\mathbf{x}),Z({\mathbf{x}}^{\prime })]={\sigma }^{2}R(\mathbf{x},{\mathbf{x}}^{\prime })\text{\hspace{1em}(5)}$$
上式中：$R(\mathbf{x},{\mathbf{x}}^{\prime })$ 为“相关函数”（类比相关系数），相关函数只与样本的空间距离有关，且满足距离为零时等于1，距离为无穷大时等于 0，相关性随着距离的增大而减小。

基于上述假设，Kriging模型寻找最优加权系数 $\mathbf{\omega }$ ，使得均方差( 用 ${\mathbf{Y}}_s=\left[\begin{array}{cccc}{Y}^{(1)}& Y^{(2)}& \dots & Y^{(n)}\end{array}\right]$ 替换 ${\mathbf{y}}_s=\left[\begin{array}{ccc}{y}^{(1)}& y^{(2)}\dots & y^{(n)}\end{array}\right]$ )
$$MSE(\hat{y}(\mathbf{x}))=E[({\mathbf{\omega }}^T{\mathbf{Y}}_s-Y(\mathbf{x}){)}^2]\text{\hspace{1em}(6)}$$
最小，并满足如下插值条件（或无偏条件）：
$$E[\sum _{i=1}^n{\omega }^{(i)}Y({\mathbf{x}}^{(i)})]=E(Y(\mathbf{x}))\text{\hspace{1em}(7)}$$
采用拉格朗日乘数法，令:
L ( ω , λ ) = E [ ( ω T Y s − Y ( x ) ) 2 ] + μ { E [ ∑ i = 1 n ω ( i ) Y ( x ( i ) ) ] − E ( Y ( x ) ) } (8) L(\omega,\lambda)=E[(\boldsymbol\omega^TY_s-Y(\mathbf x))^2] + \mu \{E[\sum_{i=1}^n\omega^{(i)}Y(\mathbf x^{(i)})]-E(Y(\mathbf x))\} \tag 8 L(ω,λ)=E[(ωTYs​−Y(x))2]+μ{E[i=1∑n​ω(i)Y(x(i))]−E(Y(x))}(8)
则由：
$$\{\begin{array}{l}\frac{\partial L(\mathbf{\omega },\mu )}{\partial {\omega }^{(i)}}=E[2({\mathbf{\omega }}^T{\mathbf{Y}}_s-Y(\mathbf{x}))Y({\mathbf{x}}^{(i)})]+\mu E[Y({\mathbf{x}}^{(i)})]=2[{\sum }_{j=1}^n({\omega }^{(j)}R({\mathbf{x}}^{(j)},{\mathbf{x}}^{(i)}+{\beta }_0^2)]-2[{\beta }_0^2+R(\mathbf{x},{\mathbf{x}}^i)]+\mu {\beta }_0=0\\ \frac{\partial L(\mathbf{\omega },\mu )}{\partial \mu }=\mu ({\beta }_0-{\beta }_0{\sum }_{i=1}^n\omega (i))=0\end{array}\text{\hspace{1em}(9)}$$

化简得：
$$\{\begin{array}{l}{\sum }_{j=1}^n{\omega }^{(j)}R({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})+\frac{\mu }{2{\sigma }^2}=R({\mathbf{x}}^{(i)},\mathbf{x})\\ {\sum }_{i=1}^n{\omega }^{(i)}=1\end{array}\text{\hspace{1em}(10)}$$
上式写成矩阵形式为：
$$\left[\begin{array}{cc}\mathbf{R}& \mathbf{F}\\ {\mathbf{F}}^T& 0\end{array}\right]\left[\begin{array}{c}\mathbf{\omega }\\ \hat{\mu }\end{array}\right]=\left[\begin{array}{c}\mathbf{r}\\ 1\end{array}\right]\text{\hspace{1em}(11)}$$
上式中：
F = [ 1    1    . . .    1 ] T ∈ R n μ ^ = μ / ( 2 σ 2 ) R = [ R ( x ( 1 ) , x ( 1 ) )    . . .    R ( x ( 1 ) , x ( n ) )             ⋮                               ⋮ R ( x ( n ) , x ( 1 )    . . .    R ( x ( n ) , x ( n ) ) ] ∈ R n × n r = [ R ( x ( 1 ) , x ) ⋮ R ( x ( n ) , x ) ] ∈ R n (12) \begin {align} &\mathbf F=[1 \ \ 1 \ \ ... \ \ 1]^T\in\R^n \\ &\hat \mu=\mu/(2\sigma^2) \\ &\mathbf R= \begin{bmatrix} R(\mathbf x^{(1)},\mathbf x^{(1)}) \ \ ... \ \ R(\mathbf x^{(1)},\mathbf x^{(n)}) \\ \ \ \ \ \ \ \ \ \ \ \ \vdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ R(\mathbf x^{(n)},\mathbf x^{(1)} \ \ ... \ \ R(\mathbf x^{(n)},\mathbf x^{(n)})\end{bmatrix} \in \R^{n \times n} \\ &\mathbf r=\begin{bmatrix}R(\mathbf x^{(1)},\mathbf x) \\ \vdots \\ R(\mathbf x^{(n)},\mathbf x) \end {bmatrix} \in \R^n \end {align}\tag{12} ​F=[1  1  ...  1]T∈Rnμ^​=μ/(2σ2)R= ​R(x(1),x(1))  ...  R(x(1),x(n))           ⋮                             ⋮R(x(n),x(1)  ...  R(x(n),x(n))​ ​∈Rn×nr= ​R(x(1),x)⋮R(x(n),x)​ ​∈Rn​(12)
则：
$$\left[\begin{array}{c}\mathbf{\omega }\\ \hat{\mu }\end{array}\right]={\left[\begin{array}{cc}\mathbf{R}& \mathbf{F}\\ {\mathbf{F}}^T& 0\end{array}\right]}^{-1}\left[\begin{array}{c}\mathbf{r}\\ 1\end{array}\right]\text{\hspace{1em}(13)}$$
其中$\left[\begin{array}{cc}\mathbf{R}& \mathbf{F}\\ {\mathbf{F}}^T& 0\end{array}\right]$ 为对称矩阵，那么：
$${\left[\begin{array}{c}\mathbf{\omega }\\ \hat{\mu }\end{array}\right]}^T=\left[\begin{array}{cc}{\mathbf{\omega }}^T& \hat{\mu }\end{array}\right]={\left[\begin{array}{c}\mathbf{r}\\ 1\end{array}\right]}^T{\left[\begin{array}{cc}\mathbf{R}& \mathbf{F}\\ {\mathbf{F}}^T& 0\end{array}\right]}^{-1}\text{\hspace{1em}(14)}$$

其中：$\mathbf{R}$ 为相关矩阵，由所有已知样本点之间的相关函数值组成，$\mathbf{r}$ 为相关矢量，由未知点与所有已知样本点之间的相关函数值组成。联立式 (3) 和式 (11)可得：
$$\hat{y}(\mathbf{x})=\left[\begin{array}{cc}{\mathbf{\omega }}^T& \hat{\mu }\end{array}\right]\left[\begin{array}{c}{\mathbf{y}}_s\\ 0\end{array}\right]={\left[\begin{array}{c}\mathbf{r}(\mathbf{x})\\ 1\end{array}\right]}^T{\left[\begin{array}{cc}\mathbf{R}& \mathbf{F}\\ {\mathbf{F}}^T& 0\end{array}\right]}^{-1}\left[\begin{array}{c}{\mathbf{y}}_s\\ 0\end{array}\right]\text{\hspace{1em}(15)}$$
由分块矩阵求逆公式：设 $\mathbf{A}$ 是 $m\times m$ 可逆矩阵，$\mathbf{B}$ 是$m\times n$ 矩阵，$\mathbf{C}$ 是 $n\times m$ 矩阵，$\mathbf{D}$ 是 $n\times n$ 可逆矩阵，则有：
$${\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]}^{-1}=\left[\begin{array}{cc}{\mathbf{A}}^{-1}+{\mathbf{A}}^{-1}\mathbf{B}(\mathbf{D}-\mathbf{C}{\mathbf{A}}^{-1}\mathbf{B}{)}^{-1}\mathbf{C}{\mathbf{A}}^{-1}& -{\mathbf{A}}^{-1}\mathbf{B}(\mathbf{D}-\mathbf{C}{\mathbf{A}}^{-1}\mathbf{B}{)}^{-1}\\ -(\mathbf{D}-\mathbf{C}{\mathbf{A}}^{-1}\mathbf{B}{)}^{-1}\mathbf{C}{\mathbf{A}}^{-1}& (\mathbf{D}-\mathbf{C}{\mathbf{A}}^{-1}\mathbf{B}{)}^{-1}\end{array}\right]\text{\hspace{1em}(16)}$$
可得：
$${\left[\begin{array}{cc}\mathbf{R}& \mathbf{F}\\ {\mathbf{F}}^T& 0\end{array}\right]}^{-1}=\left[\begin{array}{cc}{\mathbf{R}}^{-1}-{\mathbf{R}}^{-1}\mathbf{F}({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}{)}^{-1}{\mathbf{F}}^T{\mathbf{R}}^{-1}& {\mathbf{R}}^{-1}\mathbf{F}({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}{)}^{-1}\\ ({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}{)}^{-1}{\mathbf{F}}^T{\mathbf{R}}^{-1}& -({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}{)}^{-1}\end{array}\right]\text{\hspace{1em}(17)}$$
代入式 (15) 并化简可得：
$$\hat{y}(\mathbf{x})=[{\mathbf{r}}^T{\mathbf{R}}^{-1}-{\mathbf{r}}^T{\mathbf{R}}^{-1}\mathbf{F}({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}{)}^{-1}{\mathbf{F}}^T{\mathbf{R}}^{-1}+({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}{)}^{-1}{\mathbf{F}}^T{\mathbf{R}}^{-1}]{\mathbf{y}}_s\text{\hspace{1em}(18)}$$
令 ${\beta }_0=({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}{)}^{-1}{\mathbf{F}}^T{\mathbf{R}}^{-1}{\mathbf{y}}_s$，则有:
$$\hat{y}(\mathbf{x})={\beta }_0+{\mathbf{r}}^T{\mathbf{R}}^{-1}({\mathbf{y}}_s-{\beta }_0\mathbf{F})\text{\hspace{1em}(19)}$$
令列向量${\mathbf{V}}_{krig}={\mathbf{R}}^{-1}({\mathbf{y}}_s-{\beta }_0\mathbf{F})$ ，则 ${\beta }_0$ 和 ${\mathbf{V}}_{krig}$ 都只与已知样本点有关，可以在模型训练结束后一次性计算并存储。之后，预测任意 $\mathbf{x}$ 处的响应值只需要计算 $\mathbf{r}(\mathbf{x})$ 与 ${\mathbf{V}}_{krig}$ 间的点乘。

Kriging模型给出的预估值的均方差为：

$$\begin{array}{rl}MSE[\hat{y}(\mathbf{x})]& =E[({\mathbf{\omega }}^T{\mathbf{Y}}_s-\mathbf{Y}(\mathbf{x}){)}^2]\\ & =E[({\mathbf{\omega }}^T{\mathbf{Y}}_s-\mathbf{Y}(\mathbf{x}))({\mathbf{\omega }}^T{\mathbf{Y}}_s-\mathbf{Y}(\mathbf{x}))]\\ & ={\sigma }^2({\mathbf{\omega }}^T\mathbf{R}\mathbf{\omega }-2{\mathbf{\omega }}^T\mathbf{r}+1)\\ & ={\sigma }^2[{\mathbf{\omega }}^T(\mathbf{R}\mathbf{\omega }+\mathbf{F}\hat{\mu })-{\mathbf{\omega }}^T\mathbf{F}\hat{\mu }-2{\mathbf{\omega }}^T\mathbf{r}+1]\\ & ={\sigma }^2[{\mathbf{\omega }}^T\mathbf{r}-\hat{\mu }-2{\mathbf{\omega }}^T\mathbf{r}+1]\\ & ={\sigma }^2[1-{\mathbf{\omega }}^T\mathbf{r}-\hat{\mu }]\\ & ={\sigma }^2[1-[{\mathbf{\omega }}^T\hat{\mu }]\left[\begin{array}{c}\mathbf{r}\\ 1\end{array}\right]]\\ & ={\sigma }^2[1-{\left[\begin{array}{c}\mathbf{r}\\ 1\end{array}\right]}^T{\left[\begin{array}{cc}\mathbf{R}& \mathbf{F}\\ {\mathbf{F}}^T& 0\end{array}\right]}^{-1}\left[\begin{array}{c}\mathbf{r}\\ 1\end{array}\right]]\\ & ={\sigma }^2[1-{\mathbf{r}}^T{\mathbf{R}}^{-1}\mathbf{r}+(1-{\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{r}{)}^2/({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F})]\end{array}\text{\hspace{1em}(20)}$$
上述均方差可用于指导加入新样本点，以提高代理模型精度或逼近优化问题的最优解。

1.3 相关函数

在式 (19) 所示Kriging模型表达式中，相关矩阵 $\mathbf{R}$ 和相关矢量 $\mathbf{r}$ 构造涉及相关函数的选择和计算。下表为常用的相关函数：

对于高斯指数模型，参数 $\mathbf{p}=[p_1{p}_2\dots p_m{]}^T\in {\mathbb{R}}^m$ 是决定相关函数光滑程度的各向异性参数： $p_i=2$ 时，相关函数具有全局性，且无穷阶可导； $p_i<2$时，相关函数仅一阶可导。最初人们直接采用 $p_i=2$ ，虽然能获得非常光滑的插值结果，但由于相关矩阵条件数大，容易出现奇异性，导致不稳定，之后将 $p_i$ 也作为模型参数进行优化，从而提高了Kriging模型的鲁棒性。有些研究者作了进一步简化，令各方向的指数相同，即各向同性 $p_i=p,i=1,2,\dots ,m$ ，从而减少了待定模型参数，据说预测精度与简化前相当。

三次样条函数二阶可导，在光滑性和鲁棒性方面取得很好的折中。

1.4 模型参数训练

建立Kriging模型时，可以对其模型参数（也称为超参数）进行训练，可以大大增强代理模型的灵活性。一般采用“最大似然估计”或“交叉验证”。这里以最大似然估计为例进行说明，由前述引入的高斯静态随机过程的假设，在任意一点 $\mathbf{x}$ 处的响应值 $\hat{y}(\mathbf{x})$ 服从正态分布 $N({\beta }_0,{\sigma }^2)$ ，则每个样本点处的概率密度函数为：
$$P[Y(\mathbf{x})]=\frac{1}{\sqrt{2\pi }\sigma }exp\left(-\frac{(y^{(i)}-{\beta }_0{)}^2}{2{\sigma }^2}\right),i=1,\dots ,n\text{\hspace{1em}(21)}$$
则所有样本点的联合分布密度（即似然函数）为：
$$L({\beta }_0,{\sigma }^2,\mathbf{\theta },\mathbf{p})=\frac{1}{\sqrt{(2\pi {\sigma }^2{)}^n|\mathbf{R}|}}\cdot exp(-\frac{1}{2}\frac{({\mathbf{y}}_s-{\beta }_0\mathbf{F}{)}^T{\mathbf{R}}^{-1}({\mathbf{y}}_s-{\beta }_0\mathbf{F})}{{\sigma }^2})\text{\hspace{1em}(22)}$$
上式中，超参数 $\mathbf{p}$ 仅针对高斯指数函数才存在。对上式两边取对数有：
$$lnL=-\frac{1}{2}\frac{({\mathbf{y}}_s-{\beta }_0\mathbf{F}{)}^T{\mathbf{R}}^{-1}({\mathbf{y}}_s-{\beta }_0\mathbf{F})}{{\sigma }^2}-\frac{n}{2}ln({\sigma }^2)-\frac{1}{2}ln|\mathbf{R}|-\frac{n}{2}ln(2\pi )\text{\hspace{1em}(23)}$$
要使似然函数最大，令：
$$\{\begin{array}{l}\frac{\partial lnL}{\partial {\beta }_0}=\frac{1}{2{\sigma }^2}[{\mathbf{F}}^T{\mathbf{R}}^{-1}({\mathbf{y}}_s-{\beta }_0\mathbf{F})+({\mathbf{y}}_s-{\beta }_0\mathbf{F}{)}^T{\mathbf{R}}^{-1}\mathbf{F}]=\frac{1}{2{\sigma }^2}2{\mathbf{F}}^T{\mathbf{R}}^{-1}({\mathbf{y}}_s-{\beta }_0\mathbf{F})=0\\ \frac{\partial lnL}{{\sigma }^2}=\frac{1}{2}\frac{({\mathbf{y}}_s-{\beta }_0\mathbf{F}{)}^T{\mathbf{R}}^{-1}({\mathbf{y}}_s-{\beta }_0\mathbf{F})}{({\sigma }^2{)}^2}-\frac{n}{2}\frac{1}{{\sigma }^2}=0\end{array}\text{\hspace{1em}(24)}$$
解得：
$$\{\begin{array}{l}{\beta }_0(\mathbf{\theta },\mathbf{p})=({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}{)}^{-1}{\mathbf{F}}^T{\mathbf{R}}^{-1}{\mathbf{y}}_s\\ {\sigma }^2({\beta }_0,\mathbf{\theta },\mathbf{p})=\frac{1}{n}({\mathbf{y}}_s-{\beta }_0\mathbf{F}{)}^T{\mathbf{R}}^{-1}({\mathbf{y}}_s-{\beta }_0\mathbf{F})\end{array}\text{\hspace{1em}(25)}$$
将式 (25) 代入式 (23) 并忽略常数项，则最大似然函数估计是让下式最大：
$$lnL=-\frac{n}{2}ln{\sigma }^2-\frac{1}{2}ln|\mathbf{R}|\text{\hspace{1em}(26)}$$
由于无法解析地求出 $\mathbf{\theta }$ 和 $\mathbf{p}$ 的最优值，需要采用数值优化算法寻优，如梯度优化算法等。

1.5 优化加点准则

建立初始代理模型后，下一步是通过一定的加点准则循环选择新的样本点，直到优化收敛。“优化加点准则”是指如何由建立的代理模型去指导产生新的样本点的规则。以最小化优化问题为例 ，这里对最小化代理模型预测准则(MSP)、改善期望准则(EI)、改善概率准则(PI)、均方差准则(MSE)、置信下界准则(LCB)五种常用加点准则进行介绍。

1.5.1 最小化代理模型预测准则(MSP)

最小化代理模型预测准则的原理是直接在代理模型上寻找目标函数的最小值，其带约束子优化问题（子优化问题指由加点准则确定的优化问题）的数学模型为：
$$\begin{array}{rl}& min\hat{y}(\mathbf{x})\\ & s.t.\{\begin{array}{l}{\hat{g}}_i(\mathbf{x})\le 0i=1,2,\dots ,N_c\\ {\mathbf{x}}_l\le \mathbf{x}\le {\mathbf{x}}_u\end{array}\end{array}\text{\hspace{1em}(27)}$$
上式中，$\hat{y}(\mathbf{x})$ 和 ${\hat{g}}_i(\mathbf{x})$ 分别为目标函数和约束函数的代理模型。采用梯度优化算法、遗传算法等求解上述子优化问题，可以得到代理模型上预测的目标函数最优解 ${\mathbf{x}}^{\ast }$ 。

1.5.2 改善期望准则(EI)

改善期望准则也称为高效全局优化(EGO)方法，记当前已知样本点所取得的最优目标函数值 $y_{min}$ ，并假设Kriging模型预测服从均值为 $\hat{y}(\mathbf{x})$ 、标准差为 $s(\mathbf{x})$ 的正态分布，$\hat{Y}(\mathbf{x})\in N[\hat{y}(\mathbf{x}),s^2]$ ，则其概率密度为：
$$Pdf(\hat{Y}(\mathbf{x}))=\frac{1}{\sqrt{2\pi }s(\mathbf{x})}exp(-\frac{1}{2}(\frac{\hat{Y}(\mathbf{x})-\hat{y}(\mathbf{x})}{s(\mathbf{x})}{)}^2)\text{\hspace{1em}(28)}$$
对于最小化问题，目标函数改善量$I(\mathbf{x})$定义为：
$$I=max(y_{min}-\hat{Y}(\mathbf{x}),0)\text{\hspace{1em}(29)}$$
则 $I(\mathbf{x})$ 的期望值为：
$$\begin{array}{rl}{\int }_{-\infty }^{y_{min}}Pdf\cdot I& ={\int }_{-\infty }^{y_{min}}\frac{1}{\sqrt{2\pi }s}exp(-\frac{1}{2}(\frac{\hat{Y}-\hat{y}}{s}{)}^2)\cdot (y_{min}-\hat{Y})d\hat{Y}\\ & ={\int }_{-\infty }^{y_{min}}\frac{1}{\sqrt{2\pi }s}exp(-\frac{1}{2}(\frac{\hat{Y}-\hat{y}}{s}{)}^2)\cdot y_{min}d\hat{Y}-{\int }_{-\infty }^{y_{min}}\frac{1}{\sqrt{2\pi }s}exp(-\frac{1}{2}(\frac{\hat{Y}-\hat{y}}{s}{)}^2)\cdot \hat{Y}d\hat{Y}\\ & ={\int }_{-\infty }^{y_{min}}\frac{1}{\sqrt{2\pi }}exp(-\frac{1}{2}(\frac{\hat{Y}-\hat{y}}{s}{)}^2)\cdot y_{min}d(\frac{\hat{Y}-\hat{y}}{s})+\frac{s}{\sqrt{2\pi }}{\int }_{-\infty }^{y_{min}}d(ex{p}^{-\frac{1}{2}(\frac{\hat{Y}-\hat{y}}{s})})-\frac{1}{\sqrt{2\pi }s}{\int }_{\infty }^{y_{min}}\hat{y}exp(-(\frac{\hat{Y}-\hat{y}}{s}{)}^2)d\hat{Y}\\ & =(y_{min}-\hat{y})\Phi (\frac{y_{min}-\hat{y}}{s})+s\varphi (\frac{y_{min}-\hat{y}}{s})\end{array}\text{\hspace{1em}(30)}$$
上式中，$\Phi$ 和 $\varphi$ 分别为标准正态分布累积分布函数和标准正态分布概率密度函数。上式可简化为：
$$E[I(\mathbf{x})]=\{\begin{array}{l}(y_{min}-\hat{y})\Phi (\frac{y_{min}-\hat{y}}{s})+s\varphi (\frac{y_{min}-\hat{y}}{s})s>0\\ 0s=0\end{array}\text{\hspace{1em}(31)}$$
通过求解最大化 EI 值的子优化问题：
$$\begin{array}{rl}& MaxE[I(\mathbf{x})]\\ & s.t.{\mathbf{x}}_l\le \mathbf{x}\le {\mathbf{x}}_u\end{array}\text{\hspace{1em}(32)}$$
从而可以得到新的样本点 ${\mathbf{x}}^{\ast }$ 。

当优化存在约束 $g_i(\mathbf{x})\le 0,i=1,2,\dots ,N_c$ 时，对 $g_i(\mathbf{x})$ 也需要分别建立Kriging模型，并也假定其对应的随机变量 $G_i(\mathbf{x})$ 服从均值为$g_i(\mathbf{x})$ 、标准差为 $s_{g,i}(\mathbf{x})$ 的正态分布，即 $G_i(\mathbf{x})\in N[{\hat{g}}_i(\mathbf{x}),{\hat{s}}_{g,i}^2(\mathbf{x})]$ ，其中 $g_i(\mathbf{x})$ 为 Kriging 模型预估值，${\hat{s}}_{g,i}^2(\mathbf{x})$ 为预估值的方差，那么任意点 $\mathbf{x}$ 位置处满足约束的概率为：
$$P[G_i(\mathbf{x})\le 0]=\Phi (-\frac{{\hat{g}}_i(\mathbf{x})}{s_{g,i}(\mathbf{x})})\text{\hspace{1em}(33)}$$
于是可以得到约束 EI 值：
$$E_c[I(\mathbf{x})]=E[I(\mathbf{x})\bigcap G_i\le 0]=E[I(\mathbf{x})]\cdot \prod _{i=1}^{N_c}P(G_i\le 0)\text{\hspace{1em}(34)}$$
在约束存在时，求解下述无约束子优化问题：
$$\begin{array}{rl}& MaxE[I(\mathbf{x})]\cdot \prod _{i=1}^{N_c}P[G_i\le 0]\\ & s.t.{\mathbf{x}}_l\le \mathbf{x}\le {\mathbf{x}}_u\end{array}\text{\hspace{1em}(35)}$$
从而得到新的样本点 $x^{\ast }$。

1.5.3 改善概率准则（PI）

改善概率准则方法是 EI 方法的派生方法，与 EI 准则类似，该准则通过计算目标函数改善的概率，并将改善概率最大点作为新的样本点。

目标函数改善的概率为：
$$P[I(\mathbf{x})]=\Phi (\frac{y_{min}-\hat{y}(\mathbf{x})}{s(\mathbf{x})})\text{\hspace{1em}(36)}$$
通过求解最大化 PI 值的子优化问题：
$$\begin{array}{rl}& MaxP[I(\mathbf{x})]\\ & s.t.{\mathbf{x}}_l\le \mathbf{x}\le {\mathbf{x}}_u\end{array}\text{\hspace{1em}(37)}$$
从而可以得到新的样本点 ${\mathbf{x}}^{\ast }$ 。

对于约束优化问题，可以采用与约束 EI 类似的方法进行处理，即求解下面的子优化问题：
$$\begin{array}{rl}& MaxP[I(\mathbf{x})]\cdot \prod _{i=1}^{N_c}P[G_i\le 0]\\ & s.t.{\mathbf{x}}_l\le \mathbf{x}\le {\mathbf{x}}_u\end{array}\text{\hspace{1em}(38)}$$
得到新的样本点 ${\mathbf{x}}^{\ast }$ 。

1.5.4 均方差准则（MSE）

均方差准则是直接采用Kriging模型提供的均方差估计来改善代理模型全局精度的一种加点准则，即采用子优化算法求解下述子优化问题：
$$\begin{array}{rl}& MaxMSE(\hat{y}(\mathbf{x}))\\ & s.t.{\mathbf{x}}_l\le \mathbf{x}\le {\mathbf{x}}_u\end{array}\text{\hspace{1em}(39)}$$
得到新的样本点 ${\mathbf{x}}^{\ast }$ 。

对于带约束的问题，可以引入满足约束的概率，求解下面的子优化问题：
$$\begin{array}{rl}& MaxMSE(\hat{y}(\mathbf{x}))\cdot \prod _{i=1}^{N_c}P[G_i\le 0]\\ & s.t.{\mathbf{x}}_l\le \mathbf{x}\le {\mathbf{x}}_u\end{array}\text{\hspace{1em}(40)}$$
得到新的样本点 ${\mathbf{x}}^{\ast }$ 。

1.5.5 置信下界准则（LCB）

置信下界准则方法是一种利用 Kriging 模型误差估计进行全局优化的加点准则。假设 Kriging 模型预测结果满足均值为 $\hat{y}(\mathbf{x})$ 、标准差为$s(\mathbf{x})$ 的正态分布。为了充分发掘目标函数在整个设计空间上的更小值，可将对 Kriging 模型预测的置信下界作为目标函数进行子优化，并将其最小值点作为新的样本点。LCB 函数定义为：
$$LCB(\mathbf{x})=\hat{y}(\mathbf{x})-As(\mathbf{x})\text{\hspace{1em}(41)}$$
上式中，$A$ 为一个自定义常数。当 $A\to 0,LCB\to \hat{y}(\mathbf{x})$ ，该方法退化为 MSP 方法；当 $A\to \infty ,LCB\to s(\mathbf{x})$ ，该方法退化为 MSE

方法。该准则约束的处理与 MSP 准则类似，即求解下述子优化问题：
$$\begin{array}{rl}& Min\hat{y}(\mathbf{x})-As(\mathbf{x})\\ & s.t.\{\begin{array}{l}{\hat{g}}_i(\mathbf{x})\le 0i=1,2,\dots ,N_c\\ {\mathbf{x}}_l\le \mathbf{x}\le {\mathbf{x}}_u\end{array}\end{array}\text{\hspace{1em}(42)}$$

参考文献

[1] HAN Z H. Kriging Surrogate Model and its Application to Design Optimization: A Review of Recent Progress[J]. Acta Aeronauticaet Astronautica Sinica, 2016, 37(11): 3197-3225.

[2] Ping Jiang, Qi Zhou, Xinyu Shao. Surrogate Model-Based Engineering Design and Optimization [M]. 2020.文章来源地址https://www.toymoban.com/news/detail-790651.html

到了这里，关于Kriging代理模型理论相关推导的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！