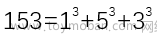人工智能概论复习笔记-Toy模板网

这篇具有很好参考价值的文章主要介绍了人工智能概论复习笔记。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

笔者精力有限，本文还没有完全完成

1.人工智能概述

人工智能概述是人工智能导论课程的第一个模块，它主要介绍了人工智能的定义、人工智能的发展历史以及人工智能的研究方向。这一部分内容旨在帮助学生了解人工智能的基本概念和背景知识。

1.1人工智能的定义

人工智能（Artificial Intelligence），英文缩写为AI。它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。人工智能是计算机科学的一个分支，它企图了解智能的实质，并生产出一种新的能以人类智能相似的方式做出反应的智能机器。根据人工智能之父约翰麦卡锡的说法，它是“制造智能机器的科学与工程，特别是智能计算机程序”

1.2人工智能的发展历史

人工智能的历史源远流长。在古代的神话传说中，技艺高超的工匠可以制作人造人，并为其赋予智能或意识。现代意义上的AI始于古典哲学家用机械符号处理的观点解释人类思考过程的尝试。20世纪40年代基于抽象数学推理的可编程数字电脑的发明使一批科学家开始严肃地探讨构造一个电子大脑的可能性。1956年，在达特茅斯学院举行的一次会议上正式确立了人工智能的研究领域

1.3人工智能的研究方向

人工智能是一个多学科交叉融合的领域，其包含机器学习、计算机视觉、自然语言处理等多个子领域。目前，实际落地比较广泛的AI领域有：计算机视觉（人脸识别、指纹识别、以图搜图、图像语义理解、目标识别等）、自然语言处理（问答系统、机器翻译等）、知识工程（知识图谱在个性化推荐、问答系统、语义搜索等场景的应用）、语音识别（AI音箱）、移动机器人（SLAM、路径规划）、工业机器人（motion planning、3D视觉）等等

2.一阶谓词逻辑知识表示法

一阶谓词逻辑知识表示法是人工智能导论课程中关于知识表示的一个重要部分。它主要介绍了命题逻辑和谓词逻辑两种逻辑形式。

2.1命题逻辑

命题逻辑是一种形式逻辑系统，它主要研究命题及其之间的关系。命题是一种陈述句，它的真值只能是真或假。命题逻辑中的基本概念包括命题、真值、逻辑联结词和真值表。

2.1.1命题

命题是一种陈述句，它的真值只能是真或假。

2.1.2真值

真值指命题的真假性。在命题逻辑中，每个命题都有一个真值，它只能是真或假。

2.1.3逻辑联结词

逻辑联结词用于连接两个或多个命题，构成新的命题。常见的逻辑联结词包括“非”（not）、“与”（and）、“或”（or）、“蕴含”（implies）和“当且仅当”（if and only if）。

2.1.4真值表

真值表是一种用于逻辑学中的数学表，特别是在连接逻辑代数、布尔函数和命题逻辑时使用。它用于计算逻辑表达式在每种论证（即每种逻辑变量取值的组合）上的值。尤其是，真值表可以用来判断一个命题表达式是否对所有允许的输入值都为真，即是否为逻辑有效的。

以下为一个真值表示例：

A	B	A AND B	A OR B
1	1	1	1
1	0	0	1
0	1	0	1
0	0	0	0

2.1.5推理规则

推理规则用于从已知命题推导出新的命题。常见的推理规则包括肯定前件（modus ponens）、否定后件（modus tollens）和假言推理（hypothetical syllogism）等。

推理规则是用于构造有效推理的方案。这些方案建立在一组称为前提的公式和称为结论的断言之间的语法关系。这些语法关系用于推理过程中，新的真实断言从其他已知的断言得出。
下面是一个简单的例子，说明了如何使用推理规则。

假设我们有以下两个前提：

如果下雨，我会带伞。
现在正在下雨。

我们可以使用一个称为“假言推理”的推理规则来推断出结论：我会带伞。

假言推理规则的形式如下：

如果P，则Q。
P。
因此，Q。

在我们的例子中，P表示“下雨”，Q表示“我会带伞”。因此，根据假言推理规则，我们可以得出结论：我会带伞。

这只是一个简单的例子，说明了如何使用推理规则。实际上，有许多不同类型的推理规则，它们可以用来构造更复杂的推理。

2.1.6证明方法

证明方法用于证明命题的真假。常见的证明方法包括直接证明、间接证明和归谬证明等。

2.1.7等价关系

等价关系用于表示两个命题在真值上相同。常见的等价关系包括德摩根定律（De Morgan’s laws）和双重否定（double negation）等。

这里有一篇不错的文章，总结了这些等价关系的常用公式。

2.2谓词逻辑

3.产生式表示法和框架表示法

产生式表示法和框架表示法是人工智能导论课程中关于知识表示的另一个重要部分。它主要介绍了两种常用的知识表示方法：产生式表示法和框架表示法。

3.1产生式表示法

产生式表示法是一种知识表示方法，它通常用于表示事实和规则。它可以表示确定性和不确定性知识。产生式系统由规则库、综合数据库和推理机三部分组成。它通过从规则库中选择可用规则与综合数据库中的已知事实进行匹配来求解问题。
规则库是产生式系统求解问题的基础，它包含了一组产生式，用于描述相应领域内的知识。综合数据库又称为事实库，用于存放问题的初始状态、原始证据、推理中得到的中间结论及最终结论等信息。推理机由一组程序组成，除了推理算法，还控制整个产生式系统的运行，实现对问题的求解。

我举个例子，用一个简单的产生式表示法表示一个医疗诊断系统。在这个系统中，规则库包含了一组产生式，每个产生式都表示一个医学规则。

IF 病人有发烧 AND 病人有咳嗽 THEN 病人可能患有感冒

在这个例子中，产生式的前提是“病人有发烧”和“病人有咳嗽”，结论是“病人可能患有感冒”。当综合数据库中包含了“病人有发烧”和“病人有咳嗽”这两个事实时，推理机会选择这条规则进行匹配，并把它推出的结论“病人可能患有感冒”加入综合数据库中。

3.2框架表示法

框架表示法是一种描述固定情况的数据结构，可以把框架看成是一个节点和关系组成的网络。它描述对于假定情况总是正确的事物，在框架的较低层次上有许多终端–被称为槽（Slots）。在槽中填入具体值，就可以得到一个描述具体事务的框架，每一个槽都可以有一些附加说明–被称为侧面（Facet），其作用是指出槽的取值范围和求值方法。

假设我们要描述一辆汽车。我们可以创建一个名为“汽车”的框架，其中包含诸如“颜色”、“品牌”和“型号”等槽。然后，我们可以在这些槽中填入具体的值，例如“红色”、“宝马”和“X5”。这样，我们就得到了一个描述具体汽车的框架。
除此之外，我们还可以在每个槽中添加侧面来指定取值范围和求值方法。例如，在“颜色”槽中，我们可以添加一个侧面来指定颜色只能是“红色”、“蓝色”或“绿色”等预定义的颜色。如果按照这个框架来描述汽车的话，就可以有如下的例子：

汽车
  颜色: 红色
  品牌: 宝马
  型号: X5

在这里，我们创建了一个名为“汽车”的框架，其中包含三个槽：“颜色”、“品牌”和“型号”。然后在这些槽中填入了具体的值，分别是“红色”、“宝马”和“X5”，这样就完成对这辆车的描述。

4.基于谓词逻辑的推理方法

基于谓词逻辑的推理方法是人工智能导论课程中关于推理方法的一个重要部分。它主要介绍了基于谓词逻辑的推理方式及其分类，以及归结演绎推理等内容。

4.1推理方式及其分类

推理是指依据一定的规则从已有的事实推出结论的过程。根据不同的标准，可以对推理进行不同的分类。常见的分类方法有以下几种：

演绎推理：**演绎推理是从一般性知识的前提出发，通过推导即“演绎”，得出具体陈述或个别结论的过程。**它是前提蕴涵结论的推理，即在推理形式有效的情况下，由真前提能够必然推出真结论的推理。
归纳推理：归纳推理是一种由个别到一般的推理。由一定程度的关于个别事物的观点过渡到范围较大的观点，由特殊具体的事例推导出一般原理、原则的解释方法。
类比推理：类比推理亦称“类推”。它是根据两个对象在某些属性上相同或相似，通过比较而推断出它们在其他属性上也相同的推理过程。

4.2归结演绎推理

归结演绎推理是一种基于逻辑“反证法”的机械化定理证明方法。其基本思想是把永真性的证明转化为不可满足性的证明。即要证明 P → Q 永真，只要能够证明 P ∧ ﹁Q 为不可满足即可。谓词公式不可满足的充要条件是其子句集不可满足。因此，要把谓词公式转换为子句集，再用鲁滨逊归结原理求解子句集是否不可满足。如果子句集不可满足，则 P → Q 永真。

接下来举一个例子来说明如何使用归结演绎推理来证明一个命题。

假设我们有以下三个前提：

所有人都会死亡。
苏格拉底是人。
苏格拉底不会死亡。

我们想要证明第三个前提是错误的。我们可以使用归结演绎推理来完成这个任务。

首先，我们将前提转换为子句集的形式：

{人(x) → 死亡(x)}
{人(苏格拉底)}
{¬死亡(苏格拉底)}

然后，我们使用鲁滨逊归结原理来对子句集进行归结。我们可以将第一个和第二个子句进行归结，得到： {死亡(苏格拉底)}

接下来，我们可以将这个新的子句与第三个子句进行归结，得到： {}

这是一个空子句，表示子句集不可满足。所以，就可以证明了第三个前提是错误的。

5.可信度方法和证据理论

可信度方法和证据理论是人工智能导论课程中关于不确定性推理的一个重要部分。它主要介绍了不确定推理、可信度方法和证据理论等内容。

5.1不确定推理

不确定推理是指从不确定性的初始证据出发，通过运用不确定性的知识，推出具有一定程度的不确定性但却是合理或近乎合理的结论的思维过程。

所有的不确定性推理方法都必须解决3个问题：表示问题、语义问题和计算问题。

1.表示问题指的是采用什么方法描述不确定性。
在专家系统中，“知识不确定性”一般分为两类：一是规则的不确定性，二是证据的不确定性。一般用 (E→H, f (H,E))来表示规则的不确定性，其中 E 是规则的前提，H 是规则的结论，f (H,E)即相应规则的不确定性程度，称为规则强度。规则强度表示了规则的可靠程度，它通常是一个数值，取值范围和具体方法取决于所采用的不确定性推理方法。一般用 (命题E, C (E))表示证据的不确定性，C (E)通常是一个数值，代表相应证据的不确定性程度，称为动态强度。规则和证据不确定性的程度常用可信度来表示。

2.语义问题指的是对表示和计算的含义进行解释。在不确定性推理中，我们需要定义一些概念和方法来描述不确定性，例如规则强度、动态强度、不确定性传递算法等。语义问题就是要求我们对这些概念和方法进行解释，指出它们的具体含义。

3.计算问题主要指不确定性的传播和更新。即计算问题定义了一组函数，求解结论的不确定性度量。计算问题主要指不确定性的传播和更新。在不确定性推理中，我们需要从初始证据出发，通过运用不确定性的知识，最终推出结论。在这个过程中，证据和知识的不确定性会传播到结论上，因此我们需要定义一组函数来计算结论的不确定性度量。这个过程包括不确定性的传递算法、结论不确定性合成和组合证据的不确定性算法等方面。
不确定性的传递算法指的是在每一步推理中，如何把证据及知识的不确定性传递给结论。在多步推理中，如何把初始证据的不确定性传递给结论。 这个过程需要定义一个函数，使得结论的不确定性度量能够根据前提的不确定性和规则强度计算出来。
结论不确定性合成指的是由两个独立的证据求得的假设的不确定性，求证据的组合导致的假设的不确定性。 这个过程需要定义一个函数，使得结论的不确定性能够根据两个独立证据求得的假设的不确定性计算出来。
组合证据的不确定性算法指的是已知两个证据的不确定性，求两个证据的析取和合取的不确定性。 这个过程需要定义两个函数，分别用于计算两个证据的析取和合取的不确定性。
下面我举一个简单的例子：

假设我们有两条规则：

如果天气晴朗，则小明会去公园玩。(E1→H1, f(H1,E1)=0.8)
如果天气阴天，则小明会在家看书。(E2→H2, f(H2,E2)=0.9)
其中 E1 表示天气晴朗，E2 表示天气阴天，H1 表示小明去公园玩，H2 表示小明在家看书。 f(H1,E1) 和 f(H2,E2) 分别表示规则 1 和规则 2 的规则强度。

现在我们知道天气晴朗这一初始证据 (E1, C(E1)=0.7)，我们想要推断出小明是否会去公园玩。

首先我们需要使用不确定性传递算法来计算结论 H1 的不确定性。由于我们只知道天气晴朗这一初始证据 (E1, C(E1)=0.7)，并没有关于天气阴天 E2 的证据，所以我们无法计算出结论 H2 的不确定性。所以我们假设 C(H2)=0。假设我们使用最大最小法，则
C(H1) = min{C(E1),f(H1,E1)} = min{0.7, 0.8} = 0.7。
然后我们可以使用结论不确定性合成来计算 H1 和 H2 的组合导致的结论 H 的不确定性。假设我们使用最大最小法，则 C(H) = max{C(H1), C(H2)} = max{0.7, 0} = 0.7。

最后我们可以使用组合证据的不确定性算法来计算 E1 和 E2 的析取和合取的不确定性。假设我们使用最大最小法，则 C(E1∧E2) = min{C(E1), C(E2)} = min{0.7, 0} = 0，C(E1∨E2) = max{C(E1), C(E2)} = max{0.7, 0} = 0.7。

5.2可信度方法

可信度方法使用可信度因子（CF）来表示规则和证据的不确定性。CF 取值范围为 [-1,1]。当 CF>0 时，表示证据的存在使得结论的可能性增大；当 CF<0 时，表示证据的存在使得结论的可能性减小；当 CF=0 时，表示证据的存在对结论的可能性无影响。
可信度方法具有简洁、直观的优点。通过简单的计算，不确定性就可以在系统中传播，并且计算具有线性的复杂度，推理的近似效果也比较理想。但是，由于可能导致计算的累计误差，如果多个规则逻辑等价于一个规则，则采用一个规则和多个规则计算的 CF 值可能就不相同。还有组合规则使用的顺序不同，可能得出不同的结果。

对于知识不确定性的表示

产生式规则表示：
IF E THEN H(CF(H,E))
CF(H,E)即可信度因子
接下来用一个简单的例子来演示可信度方法的过程。

假设我们有两条规则：

如果天气晴朗，则小明会去公园玩。(E1→H1, CF(H1,E1)=0.8)
如果天气阴天，则小明会在家看书。(E2→H2, CF(H2,E2)=0.9)

也可以写成`:

IF 天气晴朗 THEN 小明会去公园玩 (CF=0.8)
IF 天气阴天 THEN 小明会在家看书 (CF=0.9)

其中 E1 表示天气晴朗，E2 表示天气阴天，H1 表示小明去公园玩，H2 表示小明在家看书。 CF(H1,E1) 和 CF(H2,E2) 分别表示规则 1 和规则 2 的可信度。

现在我们知道天气晴朗这一初始证据 (E1, CF(E1)=0.7)，天气阴天这一初始证据(E2, CF(E2)=0.5)，我们想要推断出小明是否会去公园玩。

根据可信度方法的计算公式，CF(H2) = CF(H2,E2)×max{0,CF(E2)} = 0.9×max{0,0.5} = 0.45。

然后我们可以使用结论不确定性合成来计算 H1 和 H2 的组合导致的结论 H 的不确定性。根据可信度方法的计算公式，当 CF(H1)>0 且 CF(H2)>0 时，CF(H) = CF(H1)+CF(H2)-CF(H1)×CF(H2)；当 CF(H1)<0 且 CF(H2)<0 时，CF(H) = CF(H1)+CF(H2)+CF(H1)×CF(H2)；否则，CF(H) = (CF(H1)+CF(H2))/(1-min{|CF(H1)|,|CF(H2)|})。在这个例子中，由于 CF(H1)>0 且 CF(H2)>0，所以我们可以计算出 CF(H) = CF(H1)+CF(H2)-CF(H1)×CF(H2) = 0.56+0.45-0.56×0.45 = 0.749。

最后我们可以使用组合证据的不确定性算法来计算 E1 和 E2 的析取和合取的不确定性。根据可信度方法的计算公式，当两个证据都是合取时，CF(E) = min{CF(E1),CF(E2)}；当两个证据都是析取时，CF(E) = max{CF(E1),CF(E2)}。在这个例子中，我们可以计算出 CF(E1∧E2) = min{CF(E1),CF(E2)} = min{0.7,0.5} = 0.5，以及 CF(E1∨E2) = max{CF(E1),CF(E2)} = max{0.7,0.5} = 0.7。

5.3证据理论

证据理论（Theory of Evidence）是由Dempster首先提出，由Shafer进一步发展起来的一种不精确推理理论，也称为Dempster-Shafer (DS) 证据理论。证据理论可以在没有先验概率的情况下，灵活并有效地对不确定性建模
证据理论的核心——Dempster合成规则，能综合不同专家或者数据源的知识或者数据，这就使得证据理论在专家系统、信息融合等领域中得到了广泛应用。例如，在医学诊断、目标识别、军事指挥等许多应用领域，需要综合考虑来自多源的不确定信息，如多个传感器的信息、多位专家的意见等等，以完成问题的求解，而证据理论的联合规则在这方面的求解发挥了重要作用