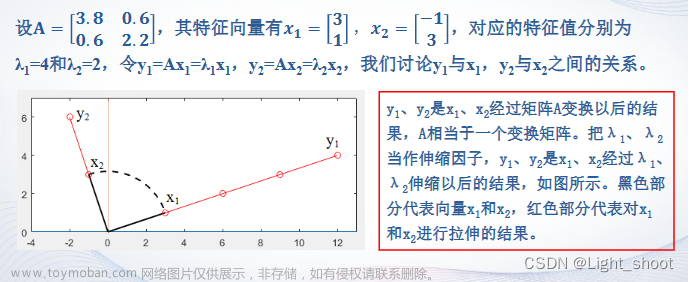
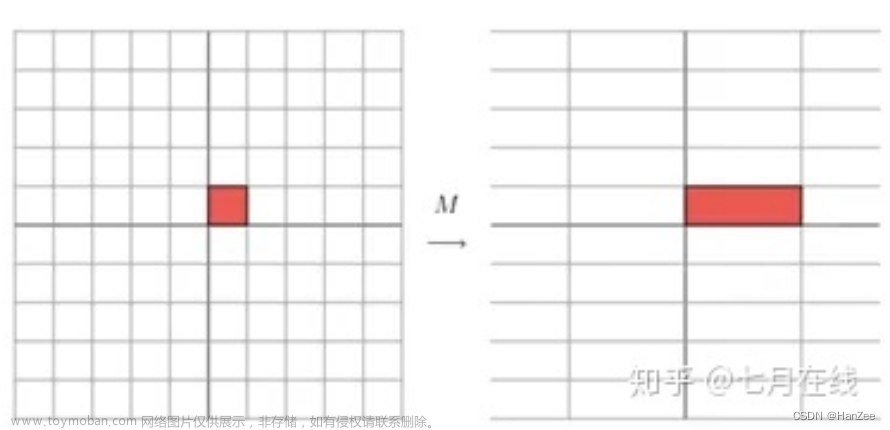
3.Hermite矩阵

Hermite矩阵

一、正规矩阵

【定义】A^H矩阵

对复矩阵 $A$
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ] A= \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} & \\ a_{21} & a_{22} & \cdots & a_{2n} & \\ \vdots & \vdots && \vdots & \\ a_{n1} & a_{n2} & \cdots & a_{nn} & \\ \end{bmatrix} A= ​a11​a21​⋮an1​​a12​a22​⋮an2​​⋯⋯⋯​a1n​a2n​⋮ann​​​ ​

有 $A^H$ 矩阵为
A H = A T ‾ = A ‾ T = [ a 11 ‾ a 12 ‾ ⋯ a 1 n ‾ a 21 ‾ a 22 ‾ ⋯ a 2 n ‾ ⋮ ⋮ ⋮ a n 1 ‾ a n 2 ‾ ⋯ a n n ‾ ] A^H=\overline{A^T}=\overline{A}^T= \begin{bmatrix} \overline{a_{11}} & \overline{a_{12}} & \cdots & \overline{a_{1n}} & \\ \overline{a_{21}} & \overline{a_{22}} & \cdots & \overline{a_{2n}} & \\ \vdots & \vdots && \vdots & \\ \overline{a_{n1}} & \overline{a_{n2}} & \cdots & \overline{a_{nn}} & \\ \end{bmatrix} AH=AT=AT= ​a11​​a21​​⋮an1​​​a12​​a22​​⋮an2​​​⋯⋯⋯​a1n​​a2n​​⋮ann​​​​ ​

【定理】 A^H的运算性质

由 $A^H$ 的定义可知：

• $(A^H{)}^H=A$
• $(A+B{)}^H=A^H+B^H$
• $(AB{)}^H=B^H{A}^H$
• $(kA{)}^H=\overline{k}{A}^H,k\in \mathbb{C}$
• $(A^H{)}^H=A$

【定义】正规矩阵、特殊的正规矩阵

正规矩阵是满足 $A^{H}A=A{A}^H$ 的矩阵，有：

• 酉矩阵：$A^{H}A=A{A}^H=E$ （参考正交矩阵 $A^{T}A=A{A}^T=E$） 是正规矩阵
• Hermite矩阵：$A^H=A$ （参考对阵矩阵 $A^H=A$）是正规矩阵
• 反Hermite矩阵：$A^H=-A$ （参考反对称矩阵/反称矩阵 $A^T=-A$）是正规矩阵
• 对角矩阵是正规矩阵

【定理】与正规矩阵酉相似的矩阵也是正规矩阵

【定理】正规的上(下)三角矩阵必为对角矩阵

【定义】复向量的内积

$<{\alpha }_j,{\alpha }_i>={\alpha }_i^H{\alpha }_j$

比如 复向量 ${\gamma }_1=[1-i,1,2{]}^T,{\gamma }_2=[1,-1,i{]}^T$，求其内积

• $<{\gamma }_1,{\gamma }_2>={\gamma }_2^H{\gamma }_1=(1,-1,-i)[1-i,1,2{]}^T=-3i$
• $<{\gamma }_2,{\gamma }_1>={\gamma }_1^H{\gamma }_2=(1+i,1,2)[1,-1,i{]}^T=3i$

【定理】Schmitt正交化

注意：下面的内积是复向量内积

${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n$（线性无关）$⟶$ ${\beta }_1,{\beta }_2,\cdots ,{\beta }_n$（正交）$⟶$ ${\eta }_1,{\eta }_2,\cdots ,{\eta }_n$（标准正交）
$${\beta }_1={\alpha }_1$$

$${\beta }_2={\alpha }_2-\frac{<{\alpha }_2,{\beta }_1>}{<{\beta }_1,{\beta }_1>}{\beta }_1$$

$${\beta }_3={\alpha }_3-\frac{<{\alpha }_3,{\beta }_2>}{<{\beta }_2,{\beta }_2>}{\beta }_2-\frac{<{\alpha }_3,{\beta }_1>}{<{\beta }_1,{\beta }_1>}{\beta }_1$$

二、酉矩阵（unitary）

酉矩阵是正交矩阵的推广

【定理】酉矩阵的判定

矩阵 $A$ 为酉矩阵当且仅当下列条件之一被满足：

• $A^{H}A=A{A}^H=E$
• $A^{-1}=A^H$

【定理】数值矩阵与酉矩阵性质的类比

数值矩阵的很多性质都可以在酉矩阵得到对应

1. 正交

• 正交矩阵 $A^{T}A=A{A}^T=E$ $\iff$ $A=[{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n]$ 是标准正交向量组（不一定非得是基）

• 酉矩阵 $A^{H}A=A{A}^H=E$ $\iff$ $A=[{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n]$ 是标准正交向量组

2. 相似

• 相似：$P^{-1}AP=B$，其中 $P$ 可逆；正交相似：$Q^{-1}AQ=Q^{T}AQ=B$，其中 $Q$ 正交
• 酉相似：$U^{H}AU=U^{-1}AU=B$，其中 $U$ 是酉矩阵

【定理】酉矩阵的所有特征值模都等于1，并且属于不同特征值的特征向量正交

这是因为在产生酉矩阵的过程中，所有的向量都进行了Schmitt正交化

【定理】Schur定理

设 $A\in {\mathbb{C}}^{n\times n}$，

则存在n阶酉矩阵 $U$，使得 $T=U^{H}AU$ 为上三角矩阵，其主对角元为 $A$ 的全部特征值

【定理】A酉相似于对角矩阵，则A为正规矩阵

设 $A\in {\mathbb{C}}^{n\times n}$，

则 $A$ 为正规矩阵当且仅当 $A$ 酉相似于对角矩阵 $diag({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)$，其中 $|{\lambda }_i|=1$

三、Hermite矩阵

【定理】Hermite矩阵的特征值必为实数，并且属于不同特征值的特征向量正交

【定理】反Hermite矩阵的特征值为0或纯虚数，并且属于不同特征值的特征向量正交

【定理】Hermite/反Hermite矩阵当且仅当的判断

设 $A\in {\mathbb{C}}^{n\times n}$，则 $A$ 为Hermite矩阵

当且仅当 $A$ 酉相似于对角矩阵 $diag({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)$，其中 ${\lambda }_i$ 均为实数，它们为 $A$ 的全部特征值

---

设 $A\in {\mathbb{C}}^{n\times n}$，则 $A$ 为反Hermite矩阵

当且仅当 $A$ 酉相似于对角矩阵 $diag({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)$，其中 ${\lambda }_i$ 的实部均为0，它们为 $A$ 的全部特征值

求酉相似对角化的酉矩阵的方法（类似本科线性代数）：
U − 1 A U = Λ = [ λ 1 λ 2 ⋱ λ n ] U^{-1}AU=\Lambda= \begin{bmatrix} \lambda_1 \\ & \lambda_2 \\ && \ddots \\ &&& \lambda_n \end{bmatrix} U−1AU=Λ= ​λ1​​λ2​​⋱​λn​​ ​
两边同时左乘 $U$ 有
$$AU=UA$$
按列分块得到
A [ η 1 , η 2 , ⋯   , η n ] = [ η 1 , η 2 , ⋯   , η n ] [ λ 1 λ 2 ⋱ λ n ] A[\eta_1,\eta_2,\cdots,\eta_n]=[\eta_1,\eta_2,\cdots,\eta_n] \begin{bmatrix} \lambda_1 \\ & \lambda_2 \\ && \ddots \\ &&& \lambda_n \end{bmatrix} A[η1​,η2​,⋯,ηn​]=[η1​,η2​,⋯,ηn​] ​λ1​​λ2​​⋱​λn​​ ​
将 $A$ 和 ${\lambda }_i$ 乘进去，得到：
$$A{\eta }_i={\lambda }_i{\eta }_i$$

四、Hermite二次型

将线性代数的实二次型扩展到复二次型

【定义】Hermite二次型

复二次型的表达式：
$$f(x_1,x_2,\cdots ,x_n)=\sum \sum a_{ij}\overline{x_i}{x}_j$$
其中 $a_{ij}=\overline{a_{ji}}$

因为
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ] A= \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{bmatrix} A= ​a11​a21​⋮an1​​a12​a22​⋮an2​​⋯⋯⋯​a1n​a2n​⋮ann​​ ​
具有性质 $A^H=A$，故 $A$ 为 Hermite 矩阵（即为 Hermite 二次型），可以写为 $f(x_1,x_2,\cdots ,x_n)=x^{H}Ax$

二次型的核心问题是怎么把二次型标准化（在一定的可逆变换下，消除掉所有的交叉项）

【定义】复相合

设 $A,B\in {\mathbb{C}}^{n\times n}$，如果存在 n 阶可逆矩阵 $Q$，使得 $Q^{H}AQ=B$，则称 $A$ 与 $B$ 复相合

【定理】每个二次型都可酉变换为标准型

任意 Hermite 二次型经过某个酉变换 $x=Uy$，$U^H=U^{-1}$，可以化为标准型 ${\lambda }_1\overline{y_1}{y}_1+{\lambda }_2\overline{y_2}{y}_2+\cdots +{\lambda }_n\overline{y_2}{y}_n$，这里 ${\lambda }_i$ 为 $A$ 的全部特征值

【定理】Hermite二次型经过适当可逆线性替换可化为规范型

Hermite二次型经过适当的可逆线性替换 $x=Qz$，这里 $Q\in {\mathbb{C}}^{n\times n}$ 为可逆矩阵，可以华为规范型：
$$f(x_1,x_2,\cdots ,x_n)=\overline{z_1}{z}_1+\cdots +\overline{z_p}{z}_p-\overline{z_{p+1}}{z}_{p+1}-\cdots \overline{z_r}{z}_r$$
这里 $r$ 为二次型 $f$ 的秩

【定理】Hermite二次型的规范型唯一

五、正定Hermite矩阵

【定义】Hermite二次型的正定、负定、半正定、半负定、不定

• 正定：如果 $\forall x\ne 0$，$x^{H}Ax>0$ 且 $x^{H}Ax=0$ 当且仅当 $x=0$，则称二次型 $f$ 为正定的
• 负定：如果 $\forall x\ne 0$，$x^{H}Ax<0$ 且 $x^{H}Ax=0$ 当且仅当 $x=0$，则称二次型 $f$ 为负定的
• 半正定：如果 $\forall x\ne 0$，$x^{H}Ax\ge 0$ 且 $\exists x\ne 0$，使得 $x^{H}Ax=0$，则称二次型 $f$ 为半正定的
• 半负定：如果 $\forall x\ne 0$，$x^{H}Ax\le 0$ 且 $\exists x\ne 0$，使得 $x^{H}Ax=0$，则称二次型 $f$ 为半负定的
• 不定：如果 $\exists x_1\ne 0$，使得 $x^{H}Ax>0$，又 $\exists x_2\ne 0$，使得 $x^{H}Ax<0$，则称二次型 $f$ 为不定的

【定理】正定、负定、半正定、半负定、不定 与 正负惯性指数 的关系

$p$ 是正惯性指数，$n$ 是负惯性指数，$r$ 是二次型的秩

• 正定 $⟺$ $p=r=n$
• 负定 $⟺$ $p=0，r=n$
• 半正定 $⟺$ $p=r<n$
• 半负定 $⟺$ $p=0，r<n$
• 不定 $⟺$ $0<p<r\le n$

【定义】Hermite矩阵的正定、负定、半正定、半负定、不定

如果 Hermite 矩阵对应的二次型是正定、负定、半正定、半负定、不定的，则该Hermite矩阵是正定、负定、半正定、半负定、不定的

【定理】正定的当且仅当条件

设 $A$ 为 n 阶矩阵，则 $A$ 为正定的当且仅当下列条件之一：文章来源地址https://www.toymoban.com/news/detail-791737.html

• $A$ 的所有特征值全部大于0
• 存在可逆矩阵 $P\in {\mathbb{C}}^{n\times n}$，使得 $P^{H}AP=E$
• 存在可逆矩阵 $Q\in {\mathbb{C}}^{n\times n}$，使得 $A=Q^{H}Q$
• $A$ 的各级顺序主子式全大于0

到了这里，关于3.Hermite矩阵的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！