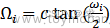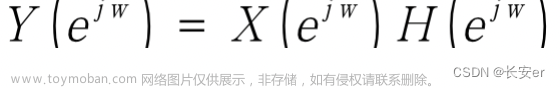1.试用Matlab计算其幅频特性和相频特性,并绘图。
代码:
n = 0:10; %定义采样点n
w = [0:1:500]*2*pi/500; % [0,pi]轴被分成1002个点
x1 = power(0.9*exp(1i*pi/3),n); %定义输入序列
x2 = exp(-1i*n); %定义一个系统的冲激响应
x = zeros(1,length(w)); %定义空数组存储系统的频域响应
for i=1:length(x1)
x=x+(x1(i)*power(x2(i),w)); %DTFT变换
end %频域相应x
H=x; %频域相应H
magH = abs(H); angH = angle(H); %幅频特性和相频特性
%在上方图窗进行绘图
subplot(2,1,1); plot(w/pi,magH); grid;
%设置横纵坐标及标题内容
xlabel('frequency in pi units'); ylabel('|H|');
title('Magnitude Response');
%在下方图窗进行绘图
subplot(2,1,2); plot(w/pi,angH/pi);grid;
%设置横纵坐标及标题内容
xlabel('frequency in pi units'); ylabel('Phase in pi Radians');
title('Phase Response');
运行结果:文章来源:https://www.toymoban.com/news/detail-791864.html

代码:
n = -10:10; %定义采样点n
w = [0:1:500]*2*pi/500; % [0,pi]轴被分成1002个点
x1 = power(0.9,n); %定义输入序列
x2 = exp(-1i*n); %定义一个系统的冲激响应
x = zeros(1,length(w)); %定义空数组存储系统的频域响应
for i=1:length(x1)
x=x+(x1(i)*power(x2(i),w));%DTFT变换
end %频域相应x
H=x; %频域相应H
magH = abs(H); angH = angle(H); %幅频特性和相频特性
%在上方图窗进行绘图
subplot(2,1,1); plot(w/pi,magH); grid;
%设置横纵坐标及标题内容
xlabel('frequency in pi units'); ylabel('|H|');
title('Magnitude Response');
%在下方图窗进行绘图
subplot(2,1,2); plot(w/pi,angH/pi);grid;
%设置横纵坐标及标题内容
xlabel('frequency in pi units'); ylabel('Phase in pi Radians');
title('Phase Response');
运行结果:

代码:
w = [0:1:500]*2*pi/500; %[0, pi]轴被分成1002个点
x=(0.5.*exp(-1i*w)).^(-2)+(0.5.*exp(-1i*w)).^(-1)+1;%信号的DTFT变换
magH= abs(x3); angH = angle(x3);%幅频特性和相频特性
%在上方图窗绘图
subplot(2,1,1); plot(w/pi,magH); grid;
%设置横纵坐标及标题内容
xlabel('frequency in pi units'); ylabel('|H|');
title('Magnitude Response');
%在下方图窗绘图
subplot(2,1,2); plot(w/pi,angH/pi); grid;
%设置横纵坐标及标题内容
xlabel('frequency in pi units'); ylabel('Phase in pi Radians');
title('Phase Response');
运行结果:

2.根据系统的单位冲击响应,用Matlab绘制系统的幅频特性和相频特性,且当
时单位冲击响应和单位阶跃响应。
代码1:
b = [1, 1, 1, 1, 1, 1]; %滤波器系数数组b
a = [5];%滤波器系数数组a
m = 0:length(b)-1; l = 0:length(a)-1; % 索引数组m和l
K = 500; k = 0:1:K; %频率的索引数组k
w = pi*k/K; %将[0, pi]范围分为501个点
num = b * exp(-j*m'*w); %频率响应的分子计算
den = a * exp(-j*l'*w); %频率响应的分母计算
H = num ./ den; %频率响应H
magH = abs(H); angH = angle(H); %幅频特性和相频特性
%在上方图窗绘图
subplot(2,1,1); plot(w/pi,magH); grid; axis([0,1,0,1]);
%设置横纵坐标以及标题内容
xlabel('frequency in pi units'); ylabel('|H|');title('Magnitude Response');
%在下方图窗绘图
subplot(2,1,2); plot(w/pi,angH/pi); grid
%设置横纵坐标以及标题内容
xlabel('frequency in pi units');ylabel('Phase in pi Radians');
title('Phase Response');
运行结果1:

代码2:
a = [5]; %滤波器系数数组a
b = [1, 1, 1, 1, 1, 1]; %滤波器系数数组b
n = [-5:10]; %定义n的范围
h = impz(b,a,n); %计算单位冲击响应
subplot(2,1,1); stem(n,h,'k');%在上方图窗绘图
%设置横纵坐标及标题内容
title('Impulse Response'); xlabel('n'); ylabel('h(n)')
x = stepseq(0,-5,10);%计算单位阶跃响应
s2 = filter(b,a,x);%对单位阶跃响应进行滤波
%在下方图窗绘图
subplot(2,1,2); stem(n,s2,'k'); axis([-5,10,0,1.5])
%设置横纵坐标及标题内容
title('Step Responsevby by filter function');xlabel('n'); ylabel('s(n)');
运行结果2:

代码1:
b = [1, 0, -1]; %滤波器系数数组b
a = [1, -0.95, -0.9025];%滤波器系数数组a
m = 0:length(b)-1; l = 0:length(a)-1; % 索引数组m和l
K = 500; k = 0:1:K; %频率的索引数组k
w = pi*k/K; %将[0, pi]范围分为501个点
num = b * exp(-j*m'*w); %频率响应的分子计算
den = a * exp(-j*l'*w); %频率响应的分母计算
H = num ./ den; %频率响应H
magH = abs(H); angH = angle(H); % 幅频特性和相频特性
%在上方图窗绘图
subplot(2,1,1); plot(w/pi,magH); grid; axis([0,1,0,1]);
%设置横纵坐标以及标题内容
xlabel('frequency in pi units'); ylabel('|H|');title('Magnitude Response');
%在下方图窗绘图
subplot(2,1,2); plot(w/pi,angH/pi); grid
%设置横纵坐标以及标题内容
xlabel('frequency in pi units');ylabel('Phase in pi Radians');
title('Phase Response');
运行结果1:

代码2:
a = [1, -0.95, -0.9025]; %滤波器系数数组a
b = [1, 0, -1]; %滤波器系数数组b
n = [-5:10]; %定义n的范围
h = impz(b,a,n); %计算单位冲击响应
%在上方图窗绘图
subplot(2,1,1); stem(n,h,'k');axis([-5,10,0,35]);
%设置横纵坐标及标题内容
title('Impulse Response'); xlabel('n'); ylabel('h(n)')
x = stepseq(0,-5,10);%计算单位阶跃响应
s2 = filter(b,a,x);%对单位阶跃响应进行滤波
%在下方图窗绘图
subplot(2,1,2); stem(n,s2,'k');
%设置横纵坐标及标题内容
title('Step Responsevby by filter function');xlabel('n'); ylabel('s(n)');
运行结果2:

3.LTI的差分方程如下,用Matlab绘制系统的幅频特性和相频特性,并求解下列输入序列的稳态响应。
代码:
b = [1, 0, 1, 0, 1, 0, 1]; %滤波器系数数组b
a = [2, 0, 0.81, 0, 0.6561, 0, 0.531441];%滤波器系数数组a
m = 0:length(b)-1; l = 0:length(a)-1; % 索引数组m和l
K = 500; k = 0:1:K; %频率的索引数组k
w = pi*k/K; %将[0, pi]范围分为501个点
num = b * exp(-j*m'*w); %频率响应的分子计算
den = a * exp(-j*l'*w); %频率响应的分母计算
H = num ./ den; %频率响应H
magH = abs(H); angH = angle(H); % 幅频特性和相频特性
%在上方图窗绘图
subplot(2,1,1); plot(w/pi,magH); grid; axis([0,1,0,1]);
%设置横纵坐标以及标题内容
xlabel('frequency in pi units'); ylabel('|H|');title('Magnitude Response');
%在下方图窗绘图
subplot(2,1,2); plot(w/pi,angH/pi); grid
%设置横纵坐标以及标题内容
xlabel('frequency in pi units'); ylabel('Phase in pi Radians');
title('Phase Response');
运行结果:

输入序列为:
代码:
b = [1, 0, 1, 0, 1, 0, 1]; %滤波器系数数组b
a = [2, 0, 0.81, 0, 0.6561, 0, 0.531441];%滤波器系数数组a
n = 0:50;%定义n的取值
x = 5 + 10 * power(-1, n); %定义输入序列
y = filter(b,a,x); %计算稳态响应
%绘制图形
stem(n, y, 'g' ,'filled');
%设置横纵坐标及标题内容
xlabel('n');ylabel('y(n)');
title('5 + 10 * (-1)^n 的稳态响应');
运行结果:

代码:
b = [1, 0, 1, 0, 1, 0, 1]; %滤波器系数数组b
a = [2, 0, 0.81, 0, 0.6561, 0, 0.531441];%滤波器系数数组a
n = 0:50;%定义n的取值
x = 1 + cos(0.5*pi*n + 1/(2*pi)); %定义输入序列
y = filter(b,a,x); %计算稳态响应
%绘制图形
stem(n, y, 'r','filled');
%设置横纵坐标及标题内容
xlabel('n');ylabel('y(n)');
title('1 + cos(0.5*pi*n + 1/(2*pi))的稳态响应');
运行结果:

代码:
b = [1, 0, 1, 0, 1, 0, 1]; %滤波器系数数组b
a = [2, 0, 0.81, 0, 0.6561, 0, 0.531441];%滤波器系数数组a
n = 0:50;%定义n的取值
x = 2*sin(n*pi/4) + 3*cos(3*pi*n/4); %定义输入序列
y = filter(b,a,x); %计算稳态响应
%绘制图形
stem(n, y, 'p','filled');
%设置横纵坐标及标题内容
xlabel('n');ylabel('y(n)');
title('2*sin(n*pi/4) + 3*cos(3*pi*n/4)的稳态响应');
运行结果:
 文章来源地址https://www.toymoban.com/news/detail-791864.html
文章来源地址https://www.toymoban.com/news/detail-791864.html
到了这里,关于数字信号处理实验---LSI系统的分析 Matlab代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!