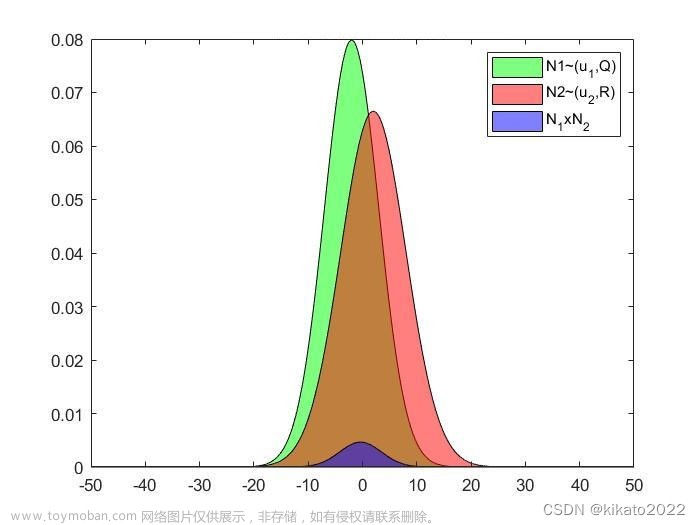
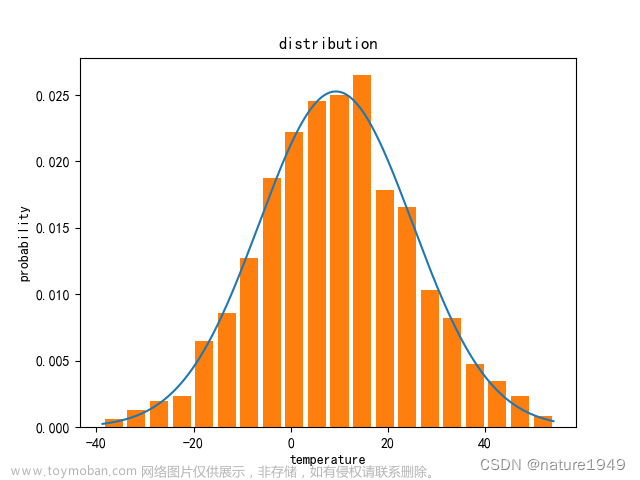
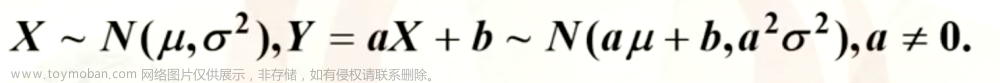公式(Z(a) = -Z(1-a)) 表示正态分布的上(a)分位点与下(1-a)分位点在分布曲线上关于均值的对称性。
-
左侧 (Z(a))： 这是分布曲线上累积概率为(a)的那个点。也就是说，这是一个使得这个点及其左侧的面积占据整个曲线下方(a)的位置。
-
右侧 (Z(1-a))： 这是分布曲线上累积概率为(1-a)的点。它位于左侧 (Z(a)) 的对称位置，使得右侧的面积占据整个曲线下方(1-a)。
-
负号的作用： 负号表示这两个点在均值的不同方向。左侧 (Z(a)) 通常是正数，表示在均值的右侧；而右侧 (Z(1-a)) 通常是负数，表示在均值的左侧。负号就是将右侧 (Z(1-a)) 的位置调整到与左侧 (Z(a)) 对称。
-
对称性理解： 在标准正态分布中，分布曲线是关于均值对称的。因此，(Z(a) = -Z(1-a)) 表示左侧 (Z(a)) 和右侧 (Z(1-a)) 在均值两侧关于对称轴对称。
-
应用场景： 这个公式在统计学中常用于计算双侧置信区间。当我们想要找到一个区间，使得这个区间两侧的面积分别为(a/2)时，就可以利用这个对称性，使用 (Z(a) = -Z(1-a)) 的关系。文章来源：https://www.toymoban.com/news/detail-791985.html
总体来说，这个公式反映了正态分布曲线的对称性质，使得上(a)分位点和下(1-a)分位点在均值两侧关于对称轴对称。
文章来源地址https://www.toymoban.com/news/detail-791985.html
到了这里，关于概率论之 证明 正态分布的上a 分位点的对称的性质的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
