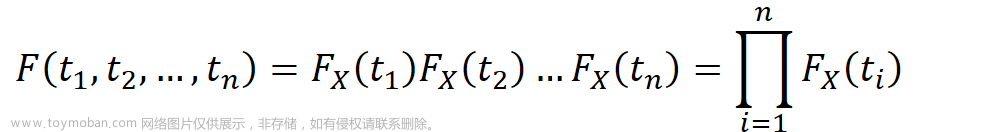VAE损失函数的推导
VAE最原始的优化目标
我们从解码器的角度来引出VAE的优化目标，即传入一个变量z，我们期待解码器能生成我们所期望生成的数据。
我们举个简单的例子来说明一下：假设在我们当前的任务下解码器的目标是根据输入的z来生成一张手写数字图片。当我们传入z之后，解码器的输出可能是各种各样的，但我们希望解码器能生成手写数字图片，而不是生成一个汉字或者是其他奇奇怪怪的符号，而这就是VAE的最原始的优化目标。
我们使用p代表解码器，p(x|z)代表给定z时解码器产生x的概率，其中x并非一个具体的值，而可以看作是一类数据，比如在我们上述的例子中，x可以代表某种风格的手写体数字，p(x|z)就是生成这些数字的概率，这里的概率也并非一个具体的值，而是某一风格的每个数字对应了一个概率，其输出的是一个概率分布。
当我们明白了这些时，我们就可以写出来VAE的优化目标，即最大化解码器输出x的概率，即最大化p(x)。
损失函数推导前的准备
我们可以将p(x)其改写为包含了传入参数的形式，即
当我们将z从离散分布变为连续分布时，该式就变成了
这里的p(z)可以是任意分布，在VAE中我们常常假设p(z)服从标准正态分布。
我们同时也需要知道KL散度的一些相关知识：KL散度用于衡量两个分布之间的差异，其值越大则两个分布的差异越大，同时两个分布的KL散度非负。计算a、b两个分布的KL散度的公式如下
损失函数的推导其一
为了最大化p(x)，我们可以采用极大似然估计的方法来进行，即最大化
对应于我们之前给的例子，这里的每个x可以代表了某一个风格的手写体，我们的目标是生成手写体数字，因此我们并不会局限其风格，只要生成的正确就要最大化其概率。
由于最大化L即相当于最大化log p(x)，因此后续目标调整为最大化log p(x)。我们假设q代表了编码器，q(z|x)就代表了给定x时编码器产生z的概率。由于
即不管给定何种x，其产生不同z的概率之和恒为1。又因为p(x)与z无关，因此我们可以将log p(x)改写为如下的形式。
由于p(x) = p(x, z) / p(z|x) = (p(x, z) / q(z|x)) * (q(z|x) / p(z|x))
其中第一次变化使用了概率论的定理，第二次变化仅仅加入了一个中间项，可以直接约分掉，并不影响结果。
此时我们可以将log p(x)写为如下形式。
我们将log里的乘积拆开，变为两项之和，即
结合之前提到过的KL散度相关的知识，我们可以看出第二项其实就是KL(q(z|x) || p(z|x))。因为该值为非负项，所以log p(x)不可能小于第一项，我们使用Lb来指代第一项，从而便于书写。
结合我们在准备阶段所提到的
我们可以知道，当p(x|z)不变时，p(x)也不变，从而log p(x)也不变，那么Lb+KL(q(z|x) || p(z|x))的值就不会变。这时如果我们利用q(z|x)来最大化Lb，那么Lb就会增大，而KL(q(z|x) || p(z|x))的值就会减小。
那么如果q(z|x)不变呢？此时当我们增大p(x|z)时，Lb会增大且p(x)会增大，即log p(x)也会增大。
由此我们可以得出结论，只要我们最大化Lb就能使log p(x)最大化。
损失函数的推导其二
此时我们的目标变为了最大化Lb。
由于p(x,z)=p(z)*p(x|z)，我们将Lb中的p(x,z)替换为p(z)*p(x|z)，并将其从log里的拆开，可以得到如下结果
我们可以看出Lb的第一项为-KL(q(z|x) || p(z))，即q(z|x)与p(z)两个分布之间的Kl散度的相反数。Lb的第二项可以看作是在q(z|x)这个分布下log p(x|z)的期望，即
此时VAE的最终目标就一目了然了，VAE的训练目标有两个：
第一，最小化KL(q(z|x) || p(z))，使q(z|x)的分布尽量向p(z)靠近。
第二，最大化在q(z|x)这个分布下log p(x|z)的期望，其中q(z|x)为编码器输入x时产生z的概率。假设解码器利用z生成出了x’，我们就需要使x’尽可能向x靠近，以最大化log p(x|z)。
实际使用时所用到的损失函数
根据上述的两个训练目标，VAE的损失函数也被设计为两个：
- L1用于最小化KL(q(z|x) || p(z))，VAE假设q(z|x)的分布为正态分布，而p(z)为标准正态分布。计算两个正态分布之间的KL散度的公式如下：
由于此处p(z)为标准正态分布，因此其μ为0，σ为1，那么我们带入后可得
其中σ为q(z|x)的标准差，μ为q(z|x)的均值。
实际实现时，当编码器接收到x时，我们并不会让编码器直接输出对应的z，而是会使编码器输出z的分布的均值和标准差，此时我们就可以使用上述的式子作为损失函数，从而更新编码器参数。文章来源：https://www.toymoban.com/news/detail-792360.html
此时我们得到了第一个损失函数。
在训练解码器时，我们会从标准正态分布中随机取样，使其乘上上述得到的方差，之后使其加上上述的均值，以此来构建解码器的输入，这样做相当于是给输入加上了噪音，使得解码器的稳定性更好。
2. L2使解码器输出的x’尽可能向x靠近，要做到这个，我们只需要最小化x’和x之间的均方误差即可，即
文章来源地址https://www.toymoban.com/news/detail-792360.html
损失函数的代码实现
def loss_function(recon, x, mu, std) -> torch.Tensor:
"""
:param recon: output of the decoder
:param x: encoder input
:param mu: mean
:param std: standard deviation
:return:
"""
recon_loss = torch.nn.functional.mse_loss(recon, x, reduction="sum")
kl_loss = -0.5 * (1 + 2 * torch.log(std) - mu.pow(2) - std.pow(2))
kl_loss = torch.sum(kl_loss)
loss = recon_loss + kl_loss
return loss
到了这里，关于VAE损失函数的推导及实现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
