知道重要，但是就是不动。
今天告诉自己，必须开始学习了。
用这篇博文作为1月份AI学习之旅的起跑点吧。
从此，无惧AI，无惧编程。
AI之路就在脚下。
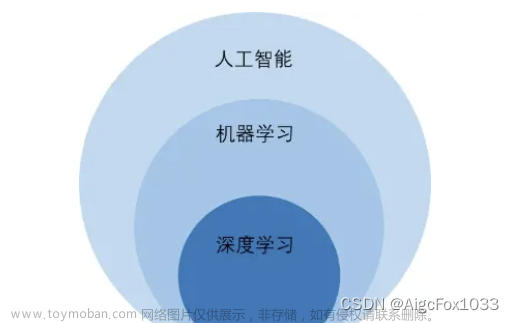
AI，在我理解，就是让机器变得更加智能，能够以人思考和行为的方式去实行某种操作，更大更快更强。
编程和AI的关系，就如同鱼与水的关系。
没有编程，AI就没有办法乖乖的听我们的话，做我们要它做的事。
编程，就相当于是发布一条条指令，指挥机器去干这个，去干那个。
机器就是一堆机械堆砌出来的玩意。他们没有感情，只会冷血的一条一条执行程序。
想让它为我所用，就得学编程。
所以，MATLAB，我来了。
反向学习：
正负1倍标准偏差的概率 =68.3%；
2、正负2倍标准偏差的概率 =95.5%；
3、正负3倍标准偏差的概率 =99.7%；
标准差是一组数值自平均值分散程度的一种测量观念。一个较大的标准差，代表大部分的数值和其平均值之间差异较大，一个较小的标准差，代表这些数值较接近平均值。
例如：
两组数的集合 {0， 5， 9， 14} 和 {5， 6， 8， 9} 其平均值都是7，但第二个集合具有较小的标准差
标准差应用于投资上，可作为量度回报稳定性的指标。标准差数值越大，代表回报远离过去平均数值，回报较不稳定故风险越高。相反，标准差数值越小，代表回报较为稳定，风险亦较小。
例如：
A，B两组各有6位学生参加同一次语文测验，A组的分数为95，85，75，65，55，45
B组的分数为73，72，71，69，68，67
这两组的平均数都是70，但A组的标准差为17.078分，B组的标准差为2.160分，说明A组学生之间的差距要比B组学生之间的差距大得多
上面的靶上有两套落点。尽管两套落点的平均中心位置都在原点 (即期望相同），但两套落点的离散程度明显有区别。蓝色的点离散程度更小。
数学上，我们用方差来代表一组数据或者某个概率分布的离散程度。可见，方差是独立于期望的另一个对分布的度量。两个分布，完全可能有相同的期望，而方差不同，正如我们上面的箭靶。文章来源：https://www.toymoban.com/news/detail-792630.html
文章来源地址https://www.toymoban.com/news/detail-792630.html
到了这里，关于我的AI之旅开始了的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
