传染病(瘟疫)经常在世界各地流行,如霍乱、天花、艾滋病、SARS、新型冠状病毒、H5N1病毒等,建立传染病的数学模型,分析其变化规律,防止其蔓延是一项艰巨的任务,这里就一般的传染规律讨论传染病的数学模型。
先从最简单的看起,
指数传播模型
为了简化模型,我们做如下假设
- 所研究区域无人员流动,无迁入迁出,不考虑出生率死亡率,区域总人口保持不变 。
- 患病人数N(t)是随时间t的连续可微函数。
- 每个病人在单位时间内传染到的人数为为常数p。
模型建立
设t时刻患病人数为N(t),t+▲t时刻患病人数为 N(t+▲t),在▲t的时间段内,患病人数为pN(t)▲t.那么就有

由于N(t)连续可微,将上述方程两边同时除以 ▲t,并且▲t趋近于0,得到微分方程

求得此模型的解析解为

适用阶段:
因为该模型表示患病人数是呈现指数型增长的,在传染病爆发初期,由于不懂得如何预防,不懂得病毒的传染方式等原因,病毒传播较快,该指数模型较为适合。
模型缺点与改进:
指数模型在t趋近与无穷时患病人数是无限增加的,这显然是不可能的,因为当健康人数减少时,单位时间内新增人数肯定是会减少的。由此我们把人均分为感染者和被感染者,建立下面的SI模型。
SI模型
为了简化模型,我们做如下假设,
- 和指数模型一样,依旧假设区域总人口N保持不变。
- 把总人群分为健康者(易感染者)和已感染者,设t时刻健康者(易感染者)和已感染者占总人口比例分别为s(t)和i(t),s(t)+i(t)=1.
- 每个病人单位时间(每天)接触平均人数为p,称为日感染率,当接触到的人为健康者,就会将其感染为病人。
- 总人数保持不变,无论是健康者还是病人,都不会死亡。
模型建立
在t到和t+▲t时刻,患病人数占据总人口比例分别为i(t),i(t+▲t),所以在这▲t时间段内,新增患病人数为Ni(t+▲t)-Ni(t).
由于病人接触的人可能为病人也可能为正常人,因此1个病人单位时间内可使ps(t)个健康人变为病人,t时刻病人总数是Ni(t),那么在▲t时间新增病人数为ps(t)Ni(t)▲t.
根据上面两条得到Ni(t+▲t)-Ni(t)=ps(t)Ni(t)▲t即

令▲t趋近于0,得到

因为s(t)+i(t)=1,

设t=0时,患病比例为i(0)=i0,则SI模型为

求解方程得到解析解

i(t)是患病人数占总人数比例,很明显t趋近于无穷时患病比例趋近于1,即所有人都被感染。
SI模型虽然把人群分为了健康者和病人,优化了指数模型中病人不断增加的缺点,但是SI模型并未考虑到病人可以被治愈,因此我们建立下面的SIS模型。
SIS模型
为了简化模型,做如下假设
- 区域总人口不变
- 把总人群分为健康者(易感染者)和已感染者,设t时刻健康者(易感染者)和已感染者占总人口比例分别为s(t)和i(t),s(t)+i(t)=1.
- 每个病人单位时间(每天)接触平均人数为p,称为日感染率,当接触到的人为健康者,就会将其感染为病人。
- 病人可以被治愈,每天被治愈人数占总人口比例为u,病人被治愈后依然可以被二次感染。
模型建立
只需在SI模型基础上减去被治愈人数

解析解为

令传染强度为

得到微分方程

解析解
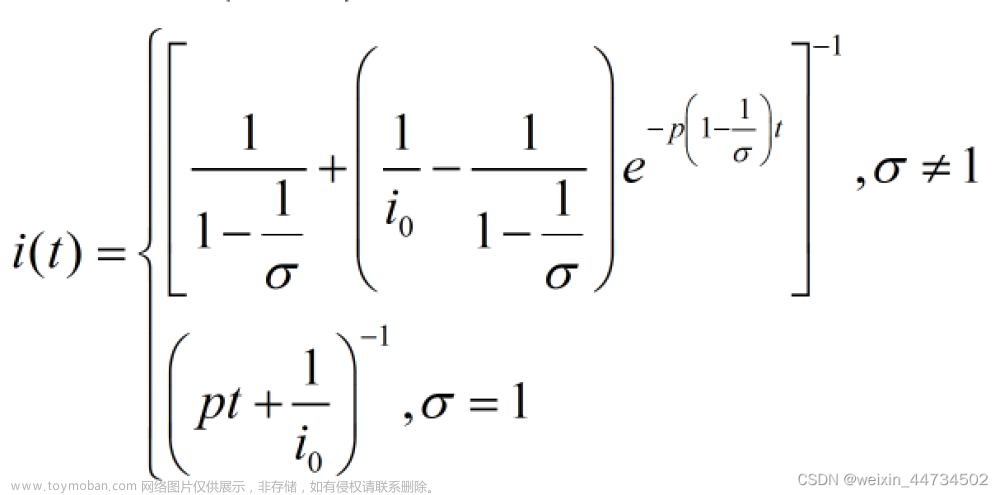
显然,传染强度是一个阈值
- 传染强度小于等于1,病人日接触率小于等于病人每日被治愈比例,即新增病人小于被治愈病人,随着时间推移,所有病人终究会被治愈。
- 传染强度大于于1,病人日接触率大于等于病人每日被治愈比例,即新增病人多于被治愈病人,随着时间推移,总有一定人口被感染成病人。
SIS假设病人可以被二次感染,但是现实中有例如天花,麻疹,肝炎等病毒在感染后会产生非常强的抗体,这些人不会再被感染,即不属于易感染者也不属于病人,这就需要用我们下面的SIR模型了。
SIR模型
为了简化模型,做如下假设,
把人群分为易感染者,病人,和有不会被感染的移除者(退出系统) ,t时刻这三种人占总人口比例为s(t),i(t),r(t),s(t)+i(t)+r(t)=1.病人日接触率为p,日治愈率为u,总人口N保持不变。
模型建立
移出者,患者,健康者人数分别为

建立微分方程传染病预测的SIR

SIR模型是多个相互关联的系统变量之间的常微分方程组,属于典型的系统动力学模型。
如果病毒具有潜伏期,那么需要多考虑一类人为潜伏者,建立SEIR模型。
文章来源地址https://www.toymoban.com/news/detail-792670.html
文章来源:https://www.toymoban.com/news/detail-792670.html
到了这里,关于微分方程传染病模型之指数模型-SI模型-SIS模型-SIR模型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!












