算法总体思想
动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题
但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解时，有些子问题被重复计算了许多次。 
如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免大量重复计算，从而得到多项式时间算法。
动态规划基本步骤
- 找出最优解的性质，并刻划其结构特征。
- 递归地定义最优值。
- 以自底向上的方式计算出最优值。
- 根据计算最优值时得到的信息，构造最优解。
矩阵连乘问题
完全加括号的矩阵连乘积可递归地定义为：
（1）单个矩阵是完全加括号的；
（2）矩阵连乘积X是完全加括号的，则X可表示为2个完全加括号的矩阵连乘积, 即Y和Z的乘积并加括号，即X=(YZ),Y和Z也是完全加括号的。
给定n个矩阵 {A1,A2,、、、An} ，其中Ai与 Ai+1是可乘的，i=1，2,、、、n-1。考察这n个矩阵的连乘积 A1A2、、、An。
由于矩阵乘法满足结合律，所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。
如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。
穷举法：
列举出所有可能的计算次序，并计算出每一种计算次序相应需要的数乘次数，从中找出一种数乘次数最少的计算次序。
算法复杂度分析：
对于n个矩阵的连乘积，设其不同的计算次序为P(n)。
由于每种加括号方式都可以分解为两个子矩阵的加括号问题：(A1...Ak)(Ak+1…An)可以得到关于P(n)的递推式如下：
（1）首先分析最优解的结构
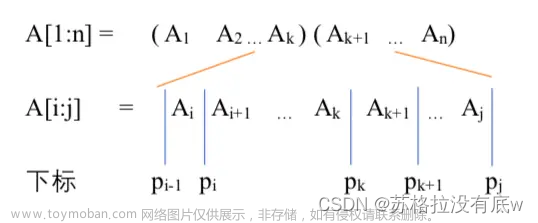
将矩阵连乘AiAi+1、、、Aj 简记为A[i:j] ，这里i≤j考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开，i≤k<j，则其相应完全加括号方式为
(AiAi+1A、、、Ak)(Ak+1Ak+2、、、Aj)
计算量：A[i:k]的计算量加上A[k+1:j]的计算量，再加上A[i:k]和A[k+1:j]相乘的计算量 
（2）建立递归关系
设计算A[i:j],1≤i≤j≤n,所需的最少数乘次数m[i,j]，则原问题的最优值为m[1,n].
（3）以自底向上的方式求最优值
用动态规划法求最优值
void MatrixChain(int *p，int n，int **m，int **s){
for (int i = 1; i <= n; i++) m[i][i] = 0;
for (int r = 2; r <= n; r++)
for (int i = 1; i <= n - r+1; i++) {
int j=i+r-1;
m[i][j] = m[i][i]+m[i+1][j]+ p[i-1]*p[i]*p[j];
s[i][j] = i;
for (int k = i+1; k < j; k++) {
int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (t < m[i][j]) { m[i][j] = t; s[i][j] = k;}
}
}
}算法复杂度分析：
算法主要计算量取决于算法中子问题的数量，已知为O（n2）,求每个子问题的最优值的时间复杂性O(n)(即k控制循环次数最大值），因此算法的计算时间上界为O(n3)。算法所占用的辅助空间显然为O(n2)。
（4）递归算法构造最优解
参考代码
#include<iostream>
#define N 20
using namespace std;
void MatrixChain(int p[N],int n,int m[N][N],int s[N][N]){
int i,j,t,k;
int r;
for(i=1;i<=n;i++){
m[i][i]=0;
}
for(r=2;r<=n;r++){
for(i=1;i<=n-r+1;i++){
j=i+r-1;
m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];
s[i][j]=i;
for(k=i+1;k<j;k++){
t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(t<m[i][j]){
m[i][j]=t;
s[i][j]=k;
}
}
}
}
}
void Traceback(int i,int j, int s[][N]){
if(i==j)
{
cout<<"A"<<i;
}
else
{
cout<<"(";
Traceback(i,s[i][j],s);
Traceback(s[i][j]+1,j,s);
cout<<")";
}
}
int main(){
int n,n1,m1,i,j=2;
int p[N]={0};
int m[N][N]={0};
int s[N][N]={0};
cout<<"Please enter the number of matrices:"<<endl;
cin>>n;
for(i=1;i<=n;i++){
cout<<"Please enter No "<<i<<"Rows and columns of matrix (n1 m1 format):";
cin>>n1>>m1;
if(i==1){
p[0]=n1;
p[1]=m1;
}
else{
p[j++]=m1;
}
}
cout<<endl<<"Record matrix rows and columns:"<<endl;
for(i=0;i<=n;i++){
cout<<p[i]<<"\t";
}
cout<<endl;
MatrixChain(p,n,m,s);
cout<<endl<<"The minimum degree matrix of matrix multiplication is:"<<endl;
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
cout<<m[i][j]<<"\t";
}
cout<<endl;
}
cout<<endl<<"The position matrix of matrix multiplication disconnection is:"<<endl;
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
cout<<s[i][j]<<"\t";
}
cout<<endl;
}
cout<<endl<<"The minimum times of matrix multiplication are:\n"<<m[1][n]<<endl;
cout<<endl;
cout<<"Disconnected position:"<<endl;
Traceback(1,n,s);
return 0;
}文章来源地址https://www.toymoban.com/news/detail-792671.html文章来源：https://www.toymoban.com/news/detail-792671.html
到了这里，关于动态规划之矩阵连乘问题C++版的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
