目录
评价类问题介绍
TOPSIS法
算法步骤
1.统一指标类型(指标正向化)
2.标准化处理
3.确定正理想解和负理想解
4.计算距离
5.计算相对接近度(S越大越接近理想解)
熵权法
概念
过程
python代码实现
作用
声明
评价类问题介绍
目的:得知一组方案的好坏,对数据评优,排序,选择
最重要步骤:权重的选择
现有A,B两名同学的各科成绩,如何评价A和B两个人谁的成绩更好?
解法是:权重*归一化后的值
归一化后的值:好得到
权重:不好得到
一般解决评价类问题采用层次分析法,但该方法的局限性在于主观性太强,不确定指标的选取为多少适宜
TOPSIS法
国内常称为优劣解距离法,它是一种常用的综合评价方法,其能充分利用原始数据的信息,其结果能精确反应各评价方案之间的差距。
如果一个方案距离理想最优解最近,距离理想最劣解最远,我们就有理由认为这个方案最好,否则就为最差的
注意:理想最优解中的数据都是各方案中的数据,而不要选择方案中没有的数据,理想最劣解同理。
算法步骤
1.统一指标类型(指标正向化)
越大越好,称为极大型指标(效益型指标)
越小越好,称为极小型指标(成本型指标)
将所有指标转化为极大型称为指标正向化
除极小型,极大型之外,另外还有中间型,区域型



2.标准化处理
-
标准化公式(消去不同指标量纲的影响)

3.确定正理想解和负理想解
找到指标的最大值和最小值

4.计算距离

优化:考虑权重
5.计算相对接近度(S越大越接近理想解)

熵权法
概念
熵的概念来自于物理学,物理意义是度量热力学系统的无序程度
熵是对不确定信息的一个度量,熵与信息量呈反比,熵值越小越好
熵权法是一种客观赋值方法。在具体使用的过程中,熵权法根据各指标的变异程度,利用信息熵计算出各指标的熵权,再通过熵权对各指标的权重进行修正,从而得到较为客观的指标权重。
信息熵小的,权重大
建模做题的时候建议使用综合主观和客观的权重,因为其更具有说服力!
过程
数据归一化处理;

python代码实现
本文为CSDN博主「笨笨洋~咩」提供的代码
详细内容请查看原文章:
https://blog.csdn.net/qq_25990967/article/details/122592159
#导入相关库
import copy
import pandas as pd
import numpy as np
#读取数据
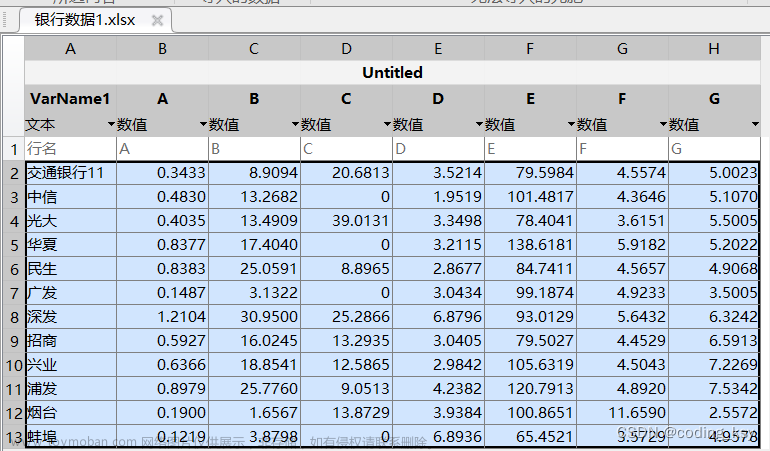
data=pd.read_excel('D:\桌面\shangquan.xlsx')
print(data)
label_need=data.keys()[2:]
print(label_need)
data1=data[label_need].values
print(data1)
#指标正向 化处理后数据为data2
data2=data1
print(data2)
#越小越优指标位置,注意python是从0开始计数,对应位置也要相应减1
index=[2,3]
for i in range(0,len(index)):
data2[:,index[i]]=max(data1[:,index[i]])-data1[:,index[i]]
print(data2)
#某点最优型指标
index1=[4]
a=90 #最优型数值
for i in range(0,len(index1)):
data2[:,index1[i]]=1-abs(data1[:,index1[i]]-a)/max(abs(data1[:,index1[i]]-a))
print(data2)
#0.002~1区间归一化
[m,n]=data2.shape
data3=copy.deepcopy(data2)
ymin=0.002
ymax=1
for j in range(0,n):
d_max=max(data2[:,j])
d_min=min(data2[:,j])
data3[:,j]=(ymax-ymin)*(data2[:,j]-d_min)/(d_max-d_min)+ymin
print(data3)
#计算信息熵
p=copy.deepcopy(data3)
for j in range(0,n):
p[:,j]=data3[:,j]/sum(data3[:,j])
print(p)
E=copy.deepcopy(data3[0,:])
for j in range(0,n):
E[j]=-1/np.log(m)*sum(p[:,j]*np.log(p[:,j]))
print(E)
# 计算权重
w=(1-E)/sum(1-E)
print(w)
#计算得分
s=np.dot(data3,w)
Score=100*s/max(s)
for i in range(0,len(Score)):
print(f"第{i}个评价对象得分为:{Score[i]}")作用
1.熵权法可对 TOPSIS 法进行修正。
2.熵权法背后的原理是利用指标的变异程度进行赋权,存在一定程度的客观性,可利用主观赋权法求得的权重向量进行综合。
3.客观赋权法存在很多,求得客观权重的方法也有很多,其中灰色关联分析法得到的关联程度也可当作权重进行应用。
4.不同的标准化方法,可能得到的标准化矩阵Z存在差异,因此根据实际情况来使用标准化方法,注意前提都是得到的Z矩阵中没有负数。
声明
本篇笔记相关图片来自于云顶数模课程,内容仅供个人学习使用
相关参考链接:
TOPSIS:
《零基础数学建模》——TOPSIS+熵权法_熵权topsis法-CSDN博客
python代码:
熵权法 —— python_熵权法python-CSDN博客
熵权法作用:文章来源:https://www.toymoban.com/news/detail-793467.html
清风数学建模学习笔记——熵权法(客观赋权法)_熵权法求权重步骤-CSDN博客文章来源地址https://www.toymoban.com/news/detail-793467.html
到了这里,关于数学建模学习笔记||TOPSIS&&熵权法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!