洛谷——P1069 [NOIP2009 普及组] 细胞分裂(分解质因数，唯一分解定理)-Toy模板网

这篇具有很好参考价值的文章主要介绍了洛谷——P1069 [NOIP2009 普及组] 细胞分裂(分解质因数，唯一分解定理)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、题目

[NOIP2009 普及组] 细胞分裂

题目描述

Hanks 博士是 BT（Bio-Tech，生物技术）领域的知名专家。现在，他正在为一个细胞实验做准备工作：培养细胞样本。

Hanks 博士手里现在有 $N$ 种细胞，编号从 $\sim N$ ，一个第 $i$ 种细胞经过 $1$ 秒钟可以分裂为 $S_i$ 个同种细胞（ $S_i$ 为正整数）。现在他需要选取某种细胞的一个放进培养皿，让其自由分裂，进行培养。一段时间以后，再把培养皿中的所有细胞平均分入 $M$ 个试管，形成 $M$ 份样本，用于实验。Hanks 博士的试管数 $M$ 很大，普通的计算机的基本数据类型无法存储这样大的 $M$ 值，但万幸的是， $M$ 总可以表示为 $m_1$ 的 $m_2$ 次方，即 $M = m_1^{m_2}$ ，其中 $m_1,m_2$ 均为基本数据类型可以存储的正整数。

注意，整个实验过程中不允许分割单个细胞，比如某个时刻若培养皿中有 $4$ 个细胞，Hanks 博士可以把它们分入 $2$ 个试管，每试管内 $2$ 个，然后开始实验。但如果培养皿中有 $5$ 个细胞，博士就无法将它们均分入 $2$ 个试管。此时，博士就只能等待一段时间，让细胞们继续分裂，使得其个数可以均分，或是干脆改换另一种细胞培养。

为了能让实验尽早开始，Hanks 博士在选定一种细胞开始培养后，总是在得到的细胞“刚好可以平均分入 $M$ 个试管”时停止细胞培养并开始实验。现在博士希望知道，选择哪种细胞培养，可以使得实验的开始时间最早。

输入格式

第一行，有一个正整数 $N$ ，代表细胞种数。

第二行，有两个正整数 $m_1,m_2$ ，以一个空格隔开，即表示试管的总数 $M = m_1^{m_2}$ 。

第三行有 $N$ 个正整数，第 $i$ 个数 $S_i$ 表示第 $i$ 种细胞经过 $1$ 秒钟可以分裂成同种细胞的个数。

输出格式

一个整数，表示从开始培养细胞到实验能够开始所经过的最少时间（单位为秒）。

如果无论 Hanks 博士选择哪种细胞都不能满足要求，则输出整数 $- 1$ 。

样例 #1

样例输入 #1

1 
2 1 
3

样例输出 #1

-1

样例 #2

样例输入 #2

2
24 1
30 12

样例输出 #2

提示

【输入输出样例 #1 说明】

经过 $1$ 秒钟，细胞分裂成 $3$ 个，经过 $2$ 秒钟，细胞分裂成 $9$ 个，……，可以看出无论怎么分裂，细胞的个数都是奇数，因此永远不能分入 $2$ 个试管。

【输入输出样例 #2 说明】

第 $1$ 种细胞最早在 $3$ 秒后才能均分入 $24$ 个试管，而第 $2$ 种最早在 $2$ 秒后就可以均分（每试管 $144 / {24}^1 = 6$ 个）。故实验最早可以在 $2$ 秒后开始。

【数据范围】

对于 $\%$ 的数据，有 $m_1^{m_2} \le 30000$ 。

对于所有的数据，有 $\le N \le 10000$ ， $\le m_1 \le 30000$ ， $\le m_2 \le 10000$ ， $\le S_i \le 2 \times {10}^9$ 。

NOIP 2009 普及组第三题

二、题解

1.基本思路：

看到数据范围暴力做肯定是不行的，不难发现细胞的分裂时指数形式的，可以表示s[i](1 秒钟可以分裂成同种细胞的个数)的t次方，t为多少秒。而试管的个数时m1的m2次方，根据唯一分解定理他们的底数都可以分解成质因数之积的形式。由于细胞要平均分入试管中，所以试管总数分解后有的质数，细胞的分解后也有，如果没有的话不能是试管的倍数。
第二个需要判断的就是细胞经过t次分裂后，分解后包含的试管总数分解后有的质数的幂次一定要大于等于试管总数分解后的质数的幂次。
唯一分解定理是在这里学的，点击链接即可跳转

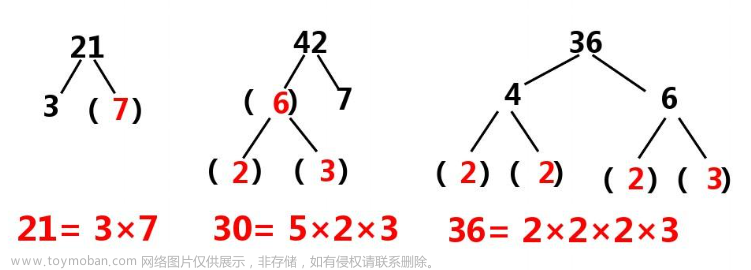
唯一分解定理是数论中一个非常重要且实用的定理,这个定理是注意描述的，任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积N=P1a1P2a2P3a3…Pnan，这里P1<P2<P3…<Pn均为质数，其中指数ai是正整数。文章来源地址https://www.toymoban.com/news/detail-793527.html

2.代码：

#include<bits/stdc++.h>
using namespace std;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long 
#define repn(i,o,n) for(int i=o;i<=n;i++)
#define rep(i,o,n) for(int i=o;i<n;i++)
const int N = 3e4+10;
//唯一分解定理是数论中一个非常重要且实用的定理
//任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有
//限个质数的乘积N=P1a1P2a2P3a3......Pnan，这里P1<P2<P3......<Pn均为质数，其中指数ai是正整数。
int p1[N],e1[N],cnt1=0;//将m1的m2次方拆分成若干质数的乘积
//p1记录质数，e1记录质数的幂，cnt1记录多少个不同的质数的乘积 
int p2[N],e2[N];// 将s[i]拆分成若干质数的乘积
//p2,e2,cnt2功能同上 
int n,m1,m2,s[N],t[N],cnt2=0,temp[N];//记录每个细胞分裂成到满足条件所需要的时间，如果n个细胞都为0,说明哪种细胞都不满足条件，输出-1
 
void divide1(int n1){
	for(int i=2;i*i<=n1;i++){
		if(n1%i==0){
			p1[++cnt1]=i,e1[cnt1]=0;
			while(n1%i==0){
				n1/=i;
				e1[cnt1]++;
			}
		}
	}
	if(n1>1)
	  p1[++cnt1]=n1,e1[cnt1]++;
	repn(i,1,cnt1)
	  e1[i]*=m2;//幂的乘法，前面求的是m1的质数幂之积，将m2乘进去即可 
//	for(int i=1;i<=cnt1;i++)
//	  cout<<p1[i]<<"^"<<e1[i]<<"  ";
//	cout<<endl;
}

void divide2(int n1){
	int cnt=0;
	for(int i=2;i*i<=n1;i++){
		if(n1%i==0){
			p2[++cnt]=i,e2[cnt]=0;
			while(n1%i==0){
				n1/=i;
				e2[cnt]++;
			}
		}
	}
	if(n1>1)
	  p2[++cnt]=n1,e2[cnt]++;
	cnt2=cnt;
//	for(int i=1;i<=cnt;i++)
//	  cout<<p2[i]<<"^"<<e2[i]<<"  ";
//	cout<<endl;
}

void solve(){
	cin>>n;//代表细胞种数
	cin>>m1>>m2;
	if(m1==1){
		cout<<0;
		return;
	}
	repn(i,1,n)
	  cin>>s[i];
	divide1(m1);
	unordered_map<int,int> mp;//m1有哪些质数 
	repn(i,1,cnt1)
	  mp[p1[i]]=e1[i];
	repn(i,1,n){
		memset(p2,0,sizeof(p2));
		memset(e2,0,sizeof(e2));
		divide2(s[i]);
		//先判断该细胞分离后可不可以均分
		int num=0;
		repn(j,1,cnt2)
		  if(mp.count(p2[j])){
		  	num++;
		  }
		if(num!=cnt1) continue;
		//可以均分，求出时间 
		int time=1;
		while(1){
			repn(j,1,cnt2)
		      temp[j]=e2[j];
			repn(j,1,cnt2)
			  temp[j]*=time;
			bool flag=true;
			repn(j,1,cnt2)
			   if(mp.count(p2[j])&&temp[j]<mp[p2[j]]){
			   	flag=false;
			   	//cout<<temp[j]<<' '<<p2[j]<<endl;
			   	break;
			   }
		 	if(flag) break;
		 	time++;  
		}
		//cout<<time<<endl;
		t[i]=time;
	}
	int ans=1LL*1<<32;
	repn(i,1,n)
	  if(t[i]&&ans>t[i])
	    ans=t[i];
	if(ans!=1LL<<32)
	  cout<<ans<<endl;
	else
	  cout<<-1<<endl;
}

signed main(){
	//IOS;
	int T=1;
	//cin>>T;
	while(T--){
		solve();
	}
	return 0;
}