评价类问题
确定评价指标、形成评价体系

- 评价的目标
- 有哪几种评价的方案
- 评价的标准/指标:题目中的背景资料、常识、网上(知网、万方、百度学术、谷歌学术)搜到的参考资料等结合 虫部落‐快搜 : https://search.chongbuluo.com/
权重分析
分而治之的思想,两个两个指标进行比较,最终根据两两比较的结果推算权重

判断矩阵
特点:
(1)𝑎ij表示的意义是,与指标𝑗相比,𝑖的重要程度。
(2)当i=j时,两个指标相同,因此同等重要记为1,这就解释了主对角线元素为1。
(3)𝑎ij> 0且满足𝑎ij*aji=1 (我们称满足这一条件的矩阵为正互反矩阵)
一致矩阵

若正互反矩阵满足aij×ajk=aik,则我们称其为一致矩阵。
特点:各行(列)之间成倍数关系
注意:在使用判断矩阵求权重之前,必须对其进行一致性检验。
一致性检验



特征值可以用matlab计算,如果特征值中有虚数,则比较的是特征值的模长
%% Matlab中求特征值和特征向量
% 在Matlab中,计算矩阵A的特征值和特征向量的函数是eig(A),其中最常用的两个用法:
A = [1 2 3 ;2 2 1;2 0 3]
% (1)E=eig(A):求矩阵A的全部特征值,构成向量E。
E=eig(A)
% (2)[V,D]=eig(A):求矩阵A的全部特征值,构成对角阵D,并求A的特征向量构成V的列向量。(V的每一列都是D中与之相同列的特征值的特征向量)
[V,D]=eig(A)
步骤:
第一步:计算一致性指标CI

第二步:查找对应的平均随机一致性指标RI

第三步:计算一致性比例CR

如果CR < 0.1, 则可认为判断矩阵的一致性可以接受;否则需要对判断矩阵进行修正
总结:
不一致如何调整:根据各行成倍数关系往一致矩阵上调整
计算权重
一致矩阵计算权重:


判断矩阵计算权重:
方法一:算术平均法求权重
第一步:将判断矩阵按照列归一化(每一个元素除以其所在列的和)
第二步:将归一化的各列相加(按行求和)
第三步:将相加后得到的向量中每个元素除以n即可得到权重向量

方法二:几何平均法求权重
第一步:将A的元素按照行相乘得到一个新的列向量
第二步:将新的向量的每个分量开n次方
第三步:对该列向量进行归一化即可得到权重向量 
方法三:特征值法求权重
第一步:求出矩阵A的最大特征值以及其对应的特征向量
第二步:对求出的特征向量进行归一化即可得到我们的权重

汇总权重计算得分
用EXCEL计算可大大减轻工作量
要点: F4可以锁定单元格
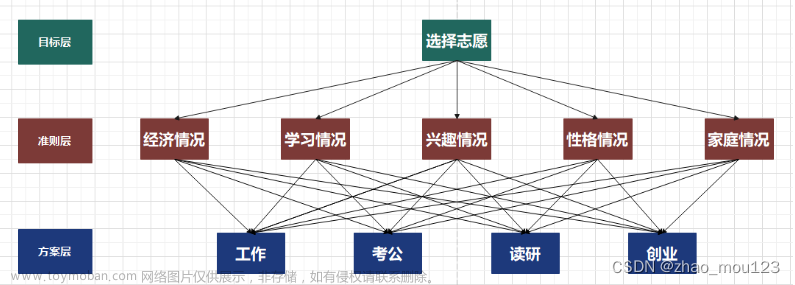
层次分析法
步骤
第一步:分析系统中各因素之间的关系,建立系统的递阶层次结构.

层次结构图制作方法:1.PPT自带SmartArt功能 2.专业软件:亿图图示或在线的ProcessOn
第二步:对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)
矩阵数据:几乎都是自己填的,在论文中直接给出来。
准则层—方案层的判断矩阵的数值要结合实际来填写,如果题目中有其他数据,可以考虑利用这些数据进行计算。
第三步:由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验(检验通过权重才能用)
三种方法计算权重:(1)算术平均法(2)几何平均法(3)特征值法
论文中加上:为了保证结果的稳健性,本文采用了三种方法分别求出了权重后计算平均值,再根据得到的权重矩阵计算各方案的得分,并进行排序和综合分析,这样避免了采用单一方法所产生的偏差,得出的结论将更全面、更有效
注:(1)一致矩阵不需要进行一致性检验,只有非一致矩阵的判断矩阵才需要进行一致性检验;
(2)在论文写作中,应该先进行一致性检验,通过检验后再计算权重,视频中讲解的只是为了顺应计算过程。
第四步:根据权重矩阵计算得分,并进行排序。
局限性
(1)评价的决策层不能太多,太多的话n会很大,判断矩阵和一致矩阵差异可能会很大。
平均随机一致性指标RI的表格中n最多是15。
(2)如果决策层中指标的数据是已知的,层次分析法不再适用
模型拓展

(1)当准则层出现多层时一层一层处理,逐渐向目标层推进
(2)当一个方案只对应一个或几个准则时,与该方案不对应的准则在矩阵中记为0
例:

代码分析
注意:在论文写作中,应该先对判断矩阵进行一致性检验,然后再计算权重,因为只有判断矩阵通过了一致性检验,其权重才是有意义的。
在下面的代码中,我们先计算了权重,然后再进行了一致性检验,这是为了顺应计算过程,事实上在逻辑上是说不过去的。
因此大家自己写论文中如果用到了层次分析法,一定要先对判断矩阵进行一致性检验。
而且要说明的是,只有非一致矩阵的判断矩阵才需要进行一致性检验。
如果你的判断矩阵本身就是一个一致矩阵,那么就没有必要进行一致性检验。(一般在论文中不会直接用一致矩阵)文章来源:https://www.toymoban.com/news/detail-793584.html
%% 输入判断矩阵
clear;clc
disp('请输入判断矩阵A: ')
% A = input('判断矩阵A=')
A =[1 1 4 1/3 3;
1 1 4 1/3 3;
1/4 1/4 1 1/3 1/2;
3 3 3 1 3;
1/3 1/3 2 1/3 1]
% matlab矩阵有两种写法,可以直接写到一行:
% [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 也可以写成多行:
[1 1 4 1/3 3;
1 1 4 1/3 3;
1/4 1/4 1 1/3 1/2;
3 3 3 1 3;
1/3 1/3 2 1/3 1]
% 两行之间以分号结尾(最后一行的分号可加可不加),同行元素之间以空格(或者逗号)分开。
%% 方法1:算术平均法求权重
% 第一步:将判断矩阵按照列归一化(每一个元素除以其所在列的和)
Sum_A = sum(A)
[n,n] = size(A) % 也可以写成n = size(A,1),求矩阵大小即条件个数n
% 因为我们的判断矩阵A是一个方阵,所以这里的r和c相同,我们可以就用同一个字母n表示
SUM_A = repmat(Sum_A,n,1) %repeat matrix的缩写,即把Sum_A看成一个整体重复n×1次构造一个n×n的新矩阵
% 另外一种替代的方法如下:
SUM_A = []; %初始化SUM_A
for i = 1:n %循环哦,这一行后面不能加冒号(和Python不同),这里表示循环n次
SUM_A = [SUM_A; Sum_A]
end
clc;A
SUM_A
Stand_A = A ./ SUM_A
% 这里我们直接将两个矩阵对应的元素相除即可
% 第二步:将归一化的各列相加(按行求和)
sum(Stand_A,2)
% 第三步:将相加后得到的向量中每个元素除以n即可得到权重向量
disp('算术平均法求权重的结果为:');
disp(sum(Stand_A,2) / n)
% 首先对标准化后的矩阵按照行求和,得到一个列向量
% 然后再将这个列向量的每个元素同时除以n即可(注意这里也可以用./哦)
%% 方法2:几何平均法求权重
% 第一步:将A的元素按照行相乘得到一个新的列向量
clc;A
Prduct_A = prod(A,2)
% prod函数和sum函数类似,一个用于乘,一个用于加 dim = 2 维度是行,即按行相乘
% 第二步:将新的向量的每个分量开n次方
Prduct_n_A = Prduct_A .^ (1/n)
% 这里对每个元素进行乘方操作,因此要加.号哦。 ^符号表示乘方哦 这里是开n次方,所以我们等价求1/n次方
% 第三步:对该列向量进行归一化即可得到权重向量
% 将这个列向量中的每一个元素除以这一个向量的和即可
disp('几何平均法求权重的结果为:');
disp(Prduct_n_A ./ sum(Prduct_n_A))
%% 方法3:特征值法求权重
% 第一步:求出矩阵A的最大特征值以及其对应的特征向量
clc
[V,D] = eig(A) %V是特征向量, D是由特征值构成的对角矩阵(除了对角线元素外,其余位置元素全为0)
Max_eig = max(max(D)) %也可以写成max(D(:))哦~
% 那么怎么找到最大特征值所在的位置了? 需要用到find函数,它可以用来返回向量或者矩阵中不为0的元素的位置索引。
% 那么问题来了,我们要得到最大特征值的位置,就需要将包含所有特征值的这个对角矩阵D中,不等于最大特征值的位置全变为0
% 这时候可以用到矩阵与常数的大小判断运算
D == Max_eig
[r,c] = find(D == Max_eig , 1)
% 找到D中第一个与最大特征值相等的元素的位置,记录它的行和列。
% 如果有两个最大特征值完全一样取其中一个即可
% 第二步:对求出的特征向量进行归一化即可得到我们的权重
V(:,c)
disp('特征值法求权重的结果为:');
disp( V(:,c) ./ sum(V(:,c)) )
% 我们先根据上面找到的最大特征值的列数c找到对应的特征向量,然后再进行标准化。
%% 计算一致性比例CR
clc
CI = (Max_eig - n) / (n-1);
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦,这里的RI最多支持 n = 15
%将RI的第二个数据改为0.001可以进行代码修正避免被除数为0时出错,判断结果是相同的
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因为CR < 0.10,所以该判断矩阵A的一致性可以接受!');
else
disp('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!');
end优化代码
disp('请输入判断矩阵A') %matlab中disp()就是屏幕输出函数,类似于c语言中的printf()函数
% 注意,disp函数比较特殊,这里可要分号,可不要分号哦
A=input('A=');
% 这里输入的就是我们的判断矩阵,其为n阶方阵(行数和列数相同)
% [1 3 1/3 1/3 1 1/3;1/3 1 1/4 1/5 1 1/5;3 4 1 1 2 3;3 5 1 1 2 1;1 1 1/2 1/2 1 1;3 5 1/3 1 1 1]
% [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 在开始下面正式的步骤之前,我们有必要检验下A是否因为粗心而输入有误
ERROR = 0; % 默认输入是没有错误的
%(1)检查矩阵A的维数是否不大于1或不是方阵
[r,c]=size(A);
%size(A)函数是用来求矩阵的大小的,返回一个行向量,第一个元素是矩阵的行数,第二个元素是矩阵的列数
%[r,c]=size(A) %将矩阵A的行数返回到第一个输出变量r,将矩阵的列数返回到第二个输出变量c
if r ~= c || r <= 1
% 注意哦,不等号是 ~= (~是键盘Tab上面那个键,要和Shift键同时按才会出来),别和C语言里面的!=搞混了
% ||表示逻辑运算符‘或’(在键盘Enter上面,也要和Shift键一起按) 逻辑运算符且是 && (&读and,连接符号,是and的缩写。 )
ERROR = 1;
end
% Matlab的判断语句,if所在的行不需要冒号,语句的最后一定要以end结尾 ;中间的语句要注意缩进。
%(2)检验是否为正互反矩阵 a_ij > 0 且 a_ij * a_ji = 1
if ERROR == 0
[n,n] = size(A);
% 因为我们的判断矩阵A是一个非零方阵,所以这里的r和c相同,我们可以就用同一个字母n表示
% 判断是否有元素小于0
% for i = 1:n
% for j = 1:n
% if A(i,j)<=0
% ERROR = 2;
% end
% end
% end
if sum(sum(A <= 0)) > 0
ERROR = 2;
end
end
%顺便检验n是否超过了15,因为RI向量为15维
if ERROR == 0
if n > 15
ERROR = 3;
end
end
if ERROR == 0
% 判断 a_ij * a_ji = 1 是否成立
if sum(sum(A' .* A ~= ones(n))) > 0
ERROR = 4;
end
% A' 表示求出 A 的转置矩阵,即将a_ij和a_ji互换位置
% ones(n)函数生成一个n*n的全为1的方阵, zeros(n)函数生成一个n*n的全为0的方阵
% ones(m,n)函数生成一个m*n的全为1的矩阵
% MATLAB在矩阵的运算中,“/”号和“*”号代表矩阵之间的乘法与除法,对应元素之间的乘除法需要使用“./”和“.*”
% 如果a_ij * a_ji = 1 满足, 那么A和A'对应元素相乘应该为1
end
if ERROR == 0
% % % % % % % % % % % % %方法1: 算术平均法求权重% % % % % % % % % % % % %
% 第一步:将判断矩阵按照列归一化(每一个元素除以其所在列的和)
% 第二步:将归一化的各列相加
% 第三步:将相加后的向量除以n即可得到权重向量
Sum_A = sum(A);
% matlab中的sum函数的用法
% a=sum(x);%按列求和
% a=sum(x,2);%按行求和
% a=sum(x(:));%对整个矩阵求和
% % 基础:matlab中如何提取矩阵中指定位置的元素?
% % (1)取指定行和列的一个元素(输出的是一个值)
% % A(2,1) A(3,2)
% % (2)取指定的某一行的全部元素(输出的是一个行向量)
% % A(2,:) A(5,:)
% % (3)取指定的某一列的全部元素(输出的是一个列向量)
% % A(:,1) A(:,3)
% % (4)取指定的某些行的全部元素(输出的是一个矩阵)
% % A([2,5],:) 只取第二行和第五行(一共2行)
% % A(2:5,:) 取第二行到第五行(一共4行)
% % (5)取全部元素(按列拼接的,最终输出的是一个列向量)
% % A(:)
SUM_A = repmat(Sum_A,n,1);
% B = repmat(A,m,n):将矩阵A复制m×n块,即把A作为B的元素,B由m×n个A平铺而成。
% 另外一种替代的方法如下:
% SUM_A = [];
% for i = 1:n %循环哦,不需要加冒号,这里表示循环n次
% SUM_A = [SUM_A;Sum_A];
% end
Stand_A = A ./ SUM_A;
% MATLAB在矩阵的运算中,“*”号和“/”号代表矩阵之间的乘法与除法,对应元素之间的乘除法需要使用“./”和“.*”
% 这里我们直接将两个矩阵对应的元素相除即可
disp('算术平均法求权重的结果为:');
disp(sum(Stand_A,2) / n)
% 首先对标准化后的矩阵按照行求和,得到一个列向量,然后再将这个列向量的每个元素同时除以n即可(注意这里也可以用./哦)
% % % % % % % % % % % % %方法2: 几何平均法求权重% % % % % % % % % % % % %
% 第一步:将A的元素按照行相乘得到一个新的列向量
Prduct_A = prod(A,2);
% prod函数和sum函数类似,一个用于乘,一个用于加
% 第二步:将新的向量的每个分量开n次方
Prduct_n_A = Prduct_A .^ (1/n);
% 这里对元素操作,因此要加.号哦。 ^符号表示乘方哦 这里是开n次方,所以我们等价求1/n次方
% 第三步:对该列向量进行归一化即可得到权重向量
% 将这个列向量中的每一个元素除以这一个向量的和即可
disp('几何平均法求权重的结果为:');
disp(Prduct_n_A ./ sum(Prduct_n_A))
% % % % % % % % % % % % %方法3: 特征值法求权重% % % % % % % % % % % % %
% 计算矩阵A的特征值和特征向量的函数是eig(A),其中最常用的两个用法:
% (1)E=eig(A):求矩阵A的全部特征值,构成向量E。
% (2)[V,D]=eig(A):求矩阵A的全部特征值,构成对角阵D,并求A的特征向量构成V的列向量。(V的每一列都是D中与之相同列的特征值的特征向量)
[V,D] = eig(A); %V是特征向量, D是由特征值构成的对角矩阵(除了对角线元素外,其余位置元素全为0)
Max_eig = max(max(D)); %也可以写成max(D(:))哦~
% 那么怎么找到最大特征值所在的位置了? 需要用到find函数,它可以用来返回向量或者矩阵中不为0的元素的位置索引。
% 下面例子来自博客:https://www.cnblogs.com/anzhiwu815/p/5907033.html
% 关于find函数的更加深入的用法可参考原文
% >> X = [1 0 4 -3 0 0 0 8 6];
% >> ind = find(X)
% ind =
% 1 3 4 8 9
% 其有多种用法,比如返回前2个不为0的元素的位置:
% >> ind = find(X,2)
% >> ind =
% 1 3
%若X是一个矩阵,索引该如何返回呢?
% >> X = [1 -3 0;0 0 8;4 0 6]
% X =
% 1 -3 0
% 0 0 8
% 4 0 6
% >> ind = find(X)
% ind =
% 1
% 3
% 4
% 8
% 9
% 这是因为在Matlab在存储矩阵时,是一列一列存储的,我们可以做一下验证:
% >> X(4)
% ans =
% -3
% 假如你需要按照行列的信息输出该怎么办呢?
% [r,c] = find(X)
% r =
% 1
% 3
% 1
% 2
% 3
% c =
% 1
% 1
% 2
% 3
% 3
% [r,c] = find(X,1) %只找第一个非0元素
% r =
% 1
% c =
% 1
% 那么问题来了,我们要得到最大特征值的位置,就需要将包含所有特征值的这个对角矩阵D中,不等于最大特征值的位置全变为0
% 这时候可以用到矩阵与常数的大小判断运算,共有三种运算符:大于> ;小于< ;等于 == (一个等号表示赋值;两个等号表示判断)
% 例如:A > 2 会生成一个和A相同大小的矩阵,矩阵元素要么为0,要么为1(A中每个元素和2比较,如果大于2则为1,否则为0)
[r,c]=find(D == Max_eig , 1);
% 找到D中第一个与最大特征值相等的元素的位置,记录它的行和列。
disp('特征值法求权重的结果为:');
disp( V(:,c) ./ sum(V(:,c)) )
% 我们先根据上面找到的最大特征值的列数c找到对应的特征向量,然后再进行标准化。
% % % % % % % % % % % % %下面是计算一致性比例CR的环节% % % % % % % % % % % % %
% 当CR<0.10时,我们认为判断矩阵的一致性可以接受;否则应对其进行修正。
CI = (Max_eig - n) / (n-1);
RI=[0 0.00001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦,这里的RI最多支持 n = 15
% 这里n=2时,一定是一致矩阵,所以CI = 0,我们为了避免分母为0,将这里的第二个元素改为了很接近0的正数
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因为CR<0.10,所以该判断矩阵A的一致性可以接受!');
else
disp('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!');
end
elseif ERROR == 1
disp('请检查矩阵A的维数是否不大于1或不是方阵')
elseif ERROR == 2
disp('请检查矩阵A中有元素小于等于0')
elseif ERROR == 3
disp('A的维数n超过了15,请减少准则层的数量')
elseif ERROR == 4
disp('请检查矩阵A中存在i、j不满足A_ij * A_ji = 1')
end注意:代码仅供参考,一定不要直接用于自己的数模论文中,国赛对于论文的查重要求非常严格,代码雷同也算作抄袭文章来源地址https://www.toymoban.com/news/detail-793584.html
到了这里,关于层次分析法(APH):评价类问题(数学建模清风笔记)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!