深入解析多目标优化技术：理论、实践与优化-Toy模板网

这篇具有很好参考价值的文章主要介绍了深入解析多目标优化技术：理论、实践与优化。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

本文深入探讨了多目标优化技术及其在机器学习和深度学习中的应用，特别聚焦于遗传算法的原理和实践应用。我们从多目标优化的基础概念、常见算法、以及面临的挑战入手，进而详细介绍遗传算法的工作原理、Python代码实现，以及如何应用于实际的机器学习模型参数优化

关注TechLead，分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验，同济本复旦硕，复旦机器人智能实验室成员，阿里云认证的资深架构师，项目管理专业人士，上亿营收AI产品研发负责人

深入解析多目标优化技术：理论、实践与优化,机器学习,人工智能,深度学习

一、引言

在现代机器学习和深度学习的世界里，优化算法扮演着核心角色。它们是推动算法向预期目标前进的引擎，无论是在精度、速度还是效率方面。但随着技术的发展，我们越来越多地面临着一个不可避免的挑战：如何在多个目标间寻找最佳平衡点。这就引出了多目标优化（Multi-Objective Optimization，简称MOO）的概念。

多目标优化技术是解决同时包含多个目标函数的优化问题的关键。这些目标往往是相互冲突的，例如，在设计一个推荐系统时，我们可能既想提高推荐的准确性，又想增加用户的多样性体验。在这种情况下，单目标优化算法就显得力不从心，因为它们通常只能优化一个目标。

多目标优化在机器学习和深度学习领域的应用日益增多，因为它们提供了一种有效的方式来平衡多个性能指标，从而在复杂的现实世界应用中实现更好的总体性能。本文旨在为资深的机器学习和深度学习从业者提供一个全面的多目标优化技术指南，包括其基础理论、主要难点、详细说明以及具体的Python代码实现。

二、多目标优化技术的基础

1. 多目标优化问题的定义

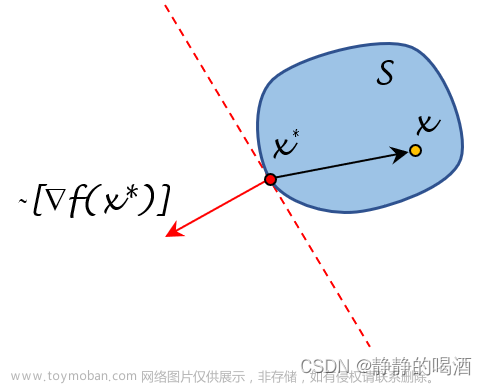
多目标优化问题（MOOP）是优化问题的一个类别，其中涉及两个或更多个相互冲突的目标函数。这些目标通常无法同时达到最优，因此解决方案涉及到在不同目标之间找到最佳折中点。例如，在自动驾驶汽车的算法开发中，安全性和响应速度就是两个需要同时考虑的目标。多目标优化的目的是找到一组“帕累托最优解”（Pareto optimal solutions），在这组解中，没有哪一个解在所有目标上都比其他解更优。

2. 常见的多目标优化算法概览

在多目标优化领域，已经发展了多种算法来处理这类问题。其中包括：

遗传算法：这类算法模仿生物进化的过程，通过选择、交叉和变异操作来进化解决方案的种群。
粒子群优化：灵感来自鸟群和鱼群的社会行为，通过模拟群体中个体的社会共享信息过程来寻找最优解。
模拟退火：模仿物质冷却过程中的原子排列，通过概率性的过程探索解空间。

每种算法都有其独特之处，适用于不同类型的多目标问题。

3. 多目标优化与单目标优化的比较

虽然多目标优化与单目标优化在核心目标——寻找最优解——上相似，但它们在处理问题的方式上存在显著差异。在单目标优化中，通常有一个明确的最优解，而在多目标优化中，则需要在多个目标之间找到一个平衡点。这使得多目标优化更加复杂，因为它需要考虑目标间的权衡和交互效应。

三、多目标优化的难点与挑战

1. 处理多个目标间的权衡

在多目标优化中，最主要的挑战之一是如何处理多个目标间的权衡。每个目标可能代表了不同的需求和优先级，它们之间可能存在天然的冲突。例如，在设计一款消费者产品时，成本和质量通常是两个需要平衡的主要目标。在这种情况下，优化算法需要能够识别和调整这些目标之间的权衡，以找到一个可接受的折中方案。这需要算法不仅要能够有效搜索解空间，还要能够在多维度目标中做出适当的选择和折中。

2. 算法的复杂性和计算资源需求

随着目标数量的增加，多目标优化问题的复杂性也随之增加。这种复杂性不仅体现在算法的设计上，还体现在对计算资源的需求上。多目标优化算法通常需要评估大量的候选解，这在计算上是非常昂贵的。此外，算法还需要能够有效地处理和存储这些解，以便于进一步的分析和决策。对于一些特别复杂或者规模特别大的问题，即使是最先进的算法和计算资源也可能难以应对。

3. 真实世界应用中的挑战

在理论研究中，多目标优化问题往往被简化或抽象化，以便于分析和求解。然而，在现实世界的应用中，这些问题可能会变得更加复杂和多变。例如，在金融领域，优化一个投资组合涉及到对风险和回报的权衡，这两个目标受到市场波动、政策变化和其他不可预测因素的影响。因此，多目标优化算法需要能够适应这种动态变化的环境，同时还要考虑到问题的特定背景和约束条件。

4. 算法的普适性和定制化

另一个挑战是如何在算法的普适性和定制化之间找到平衡。一方面，我们希望开发出能够应对各种问题的通用算法；另一方面，特定问题的特殊性又要求算法有一定的定制化能力。这就需要在算法设计时考虑到灵活性和适应性，使其能够根据不同问题的特点进行调整。同时，这也意味着从业者需要有足够的专业知识来理解和应用这些算法，以及根据具体情况进行必要的修改。

5. 算法的评估和选择

在多目标优化领域，没有一种算法可以在所有情况下都是最优的。因此，选择或者开发适合特定问题的算法是一个重要的挑战。这不仅需要深入理解问题的本质和需求，还需要对不同算法的特点和适用范围有清晰的认识。此外，评估算法的效果也是一个挑战，因为我们需要考虑到多个目标和可能的权衡。这通常涉及到复杂的评估指标和决策标准。

四、多目标优化的主流算法一览

在多目标优化领域，有几种核心算法被广泛研究和应用。这些算法各有特点，适用于解决不同类型的多目标问题。以下是几种关键算法的详细介绍：

1. 遗传算法（Genetic Algorithms, GAs）

深入解析多目标优化技术：理论、实践与优化,机器学习,人工智能,深度学习
遗传算法是启发式搜索算法的一种，灵感来源于自然选择和遗传学原理。它们通过模拟生物进化的过程来解决优化问题。

核心概念：

种群（Population）：一组候选解的集合。
适应度（Fitness）：衡量解决方案质量的函数。
选择（Selection）：根据适应度选择最佳解进行繁殖。
交叉（Crossover）：结合两个解决方案的特点生成新解。
变异（Mutation）：随机改变解决方案的部分特性以引入多样性。

算法流程：

初始化一个随机种群。
计算每个个体的适应度。
通过选择、交叉和变异操作生成新种群。
重复步骤2和3直到满足终止条件。

应用场景：
遗传算法适用于搜索空间较大或问题结构不清晰的情况。它们在解决复杂、非线性和多峰值问题方面表现出色。

2. 粒子群优化（Particle Swarm Optimization, PSO）

深入解析多目标优化技术：理论、实践与优化,机器学习,人工智能,深度学习
粒子群优化是另一种基于群体智能的优化算法，模拟鸟群和鱼群的行为。

核心概念：

粒子（Particle）：解空间中的一个候选解。
速度（Velocity）：粒子在解空间中移动的速度和方向。
个体最佳（Personal Best, pBest）：粒子历史上最优位置。
全局最佳（Global Best, gBest）：整个群体中的最优位置。

算法流程：

初始化粒子群和它们的速度。
评估每个粒子的适应度。
更新每个粒子的个体最佳和全局最佳。
调整粒子的速度和位置。
重复步骤2至4直到满足终止条件。

应用场景：
PSO在处理连续空间优化问题时非常有效，特别是当问题可用数学模型准确描述时。

3. 模拟退火（Simulated Annealing, SA）

深入解析多目标优化技术：理论、实践与优化,机器学习,人工智能,深度学习
模拟退火是一种概率性搜索算法，灵感来源于物质加热和随后的缓慢冷却过程。

核心概念：

温度（Temperature）：控制搜索过程中随机性的参数。
冷却计划（Cooling Schedule）：降低温度的时间表。

算法流程：

选择一个初始解和初始温度。
在当前解的邻域内随机选择一个新解。
根据特定准则（如Metropolis准则

）决定是否接受新解。
4. 降低温度并重复步骤2和3直到满足终止条件。

应用场景：
模拟退火适用于各种类型的优化问题，尤其是那些局部最优解众多的问题。

4. 非支配排序遗传算法 II（NSGA-II）

非支配排序遗传算法 II（NSGA-II）是一种专门为解决多目标优化问题而设计的遗传算法。

核心概念：

非支配排序（Non-dominated Sorting）：根据解的支配关系对种群进行分层排序。
拥挤度比较（Crowding Distance）：衡量解在目标空间中的分布密集程度。

算法流程：

初始化种群，并对其进行非支配排序和拥挤度计算。
选择父代，进行交叉和变异产生子代。
将父代和子代合并，并按非支配排序和拥挤度进行选择，形成新一代种群。
重复步骤2和3直到满足终止条件。

应用场景：
NSGA-II在处理具有多个目标的优化问题时非常有效，特别是在需要平衡探索和利用的情况下。

5. 多目标进化算法基于分解（MOEA/D）

多目标进化算法基于分解（MOEA/D）是将多目标优化问题分解为一系列子问题，并同时求解这些子问题的方法。

核心概念：

分解方法（Decomposition Methods）：将多目标问题分解为若干单目标问题。
邻域结构（Neighborhood Structure）：定义子问题之间的互相影响。

算法流程：

将多目标问题分解为多个单目标子问题。
初始化解，并为每个子问题分配一个解。
根据邻域结构更新解。
重复步骤3直到满足终止条件。

应用场景：
MOEA/D适用于那些可以有效分解为多个子问题的复杂多目标问题。

6. 多目标粒子群优化（MOPSO）

多目标粒子群优化（MOPSO）是粒子群优化算法的多目标版本，专门用于解决具有多个目标的优化问题。

核心概念：

外部存档（External Archive）：存储非支配解的集合。
引导粒子（Leader Selection）：选择引导其他粒子的非支配解。

算法流程：

初始化粒子群和外部存档。
评估每个粒子的适应度，并更新外部存档。
根据外部存档中的非支配解引导粒子更新位置。
重复步骤2和3直到满足终止条件。

应用场景：
MOPSO在处理那些目标间存在复杂权衡关系的问题时表现良好，尤其适用于连续目标空间的问题。

7. 多目标蚁群优化（MOACO）

多目标蚁群优化（MOACO）是基于蚁群算法的多目标优化版本，它模仿了蚂蚁寻找食物的行为。

核心概念：

信息素（Pheromone）：蚂蚁在路径上留下的信息素，用于指导其他蚂蚁。
启发式信息（Heuristic Information）：影响蚂蚁选择路径的额外信息。

算法流程：

初始化蚂蚁群和信息素矩阵。
每只蚂蚁根据信息素和启发式信息选择路径。
评估每条路径并更新信息素。
重复步骤2和3直到满足终止条件。

应用场景：
MOACO特别适用于处理离散空间的多目标问题，如调度和路径规划。

8. 多目标差分进化（MODE）

多目标差分进化（MODE）是差分进化算法的多目标版本，用于解决连续优化问题。

核心概念：

差分操作（Differential Operation）：通过组合种群中的个体产生新个体。
交叉（Crossover）：结合父代和子代个体的特性。
选择（Selection）：根据适应度选择更优个体。

算法流程：

初始化种群。
对种群中的每个个体应用差分操作、交叉和选择。
重复步骤2直到满足终止条件。

应用场景：
MODE特别适用于需要处理大量连续变量的多目标问题。

9. 多目标遗传规划（MOGP）

多目标遗传规划（MOGP）是遗传规划的多目标版本，用于自动生成计算机程序或模型。

核心概念：

程序树（Program Trees）：表示解决方案的树状结构。
遗传操作（Genetic Operations）：包括交叉和变异，用于修改程序树。

算法流程：

初始化程序树的种群。
评估每棵树的适应度。
应用遗传操作产生新一代程序树。
重复步骤2和3直到满足终止条件。

应用场景：
MOGP适用于需要自动生成或优化复杂结构或模型的场景，如符号回归和自动编程。

五、Python代码实现：遗传算法解决多目标优化问题

1.应用场景

场景描述：
假设我们需要优化一个机器学习模型的参数，以达到高准确度和低资源消耗（例如计算时间）的目标。这是一个典型的多目标优化问题，我们需要在准确度和资源消耗之间找到最佳平衡。

问题定义：

目标1：最大化模型的准确度。
目标2：最小化模型的资源消耗（例如计算时间）。

我们将使用遗传算法来同时处理这两个目标。

2.遗传算法实现

算法概述：

初始化：随机生成一组候选解（参数集）作为初始种群。
适应度评估：评估每个候选解的性能，考虑两个目标：准确度和资源消耗。
选择：根据适应度选择较好的候选解进行繁殖。
交叉和变异：应用交叉和变异操作生成新一代候选解。
重复：重复适应度评估、选择、交叉和变异步骤，直到达到预定的迭代次数。

Python代码实现：

import numpy as np
import random

# 模拟一个机器学习模型的评估函数
def evaluate_model(parameters):
    # 这里用随机数模拟评估结果
    accuracy = random.uniform(0.7, 0.99)  # 模拟准确度
    resource_consumption = random.uniform(0.1, 1.0)  # 模拟资源消耗
    return accuracy, resource_consumption

# 适应度函数
def fitness(accuracy, resource_consumption):
    # 这里我们希望准确度高且资源消耗低
    return accuracy / resource_consumption

# 初始化种群
def initialize_population(pop_size, param_size):
    return np.random.rand(pop_size, param_size)

# 选择操作
def selection(population, fitnesses, num_parents):
    parents = np.empty((num_parents, population.shape[1]))
    for parent_num in range(num_parents):
        max_fitness_idx = np.where(fitnesses == np.max(fitnesses))
        max_fitness_idx = max_fitness_idx[0][0]
        parents[parent_num, :] = population[max_fitness_idx, :]
        fitnesses[max_fitness_idx] = -999999
    return parents

# 交叉操作
def crossover(parents, offspring_size):
    offspring = np.empty(offspring_size)
    crossover_point = np.uint8(offspring_size[1]/2)
    for k in range(offspring_size[0]):
        parent1_idx = k % parents.shape[0]
        parent2_idx = (k+1) % parents.shape[0]
        offspring[k, 0:crossover_point] = parents[parent1_idx, 0:crossover_point]
        offspring[k, crossover_point:] = parents[parent2_idx, crossover_point:]
    return offspring

# 变异操作
def mutation(offspring_crossover):
    for idx in range(offspring_crossover.shape[0]):
        random_value = np.random.uniform(-1.0, 1.0, 1)
        offspring_crossover[idx, :] = offspring_crossover[idx, :] + random_value
    return offspring_crossover

# 遗传算法主函数
def genetic_algorithm(pop_size, param_size, num_generations):
    population = initialize_population(pop_size, param_size)
    for generation in range(num_generations):
        fitnesses = []
        for individual in population:
            accuracy, resource_consumption = evaluate_model(individual)
            fitnesses.append(fitness(accuracy, resource_consumption))
        parents = selection(population, np.array(fitnesses), pop_size//2)
        offspring_crossover

 = crossover(parents, (pop_size-parents.shape[0], param_size))
        offspring_mutation = mutation(offspring_crossover)
        population[0:parents.shape[0], :] = parents
        population[parents.shape[0]:, :] = offspring_mutation
    return population

# 参数设置
pop_size = 10  # 种群大小
param_size = 5  # 参数个数
num_generations = 5  # 迭代次数

# 运行遗传算法
optimized_population = genetic_algorithm(pop_size, param_size, num_generations)
print("Optimized Parameters:\n", optimized_population)

这段代码展示了如何使用遗传算法来处理一个简化的多目标优化问题。代码中包含了模型评估、适应度计算、种群初始化、选择、交叉和变异等关键步骤。

六、应用遗传算法优化机器学习模型参数

在前面的代码实现中，我们模拟了遗传算法的基本框架。现在，让我们将其应用于一个更具体的场景：优化机器学习模型的参数以达到高准确度和低计算资源消耗。

1.场景再定义

假设我们正在处理一个分类问题，我们选择了支持向量机（SVM）作为我们的机器学习模型。我们的目标是优化SVM的参数，例如C（正则化参数）和gamma（核函数参数），以获得最佳的分类性能和计算效率。

2.改进策略

为了使遗传算法在这个场景中更加有效，我们可以采取以下策略：

精确的适应度函数：适应度函数需要精确地反映出模型性能和资源消耗。我们可以使用交叉验证准确率作为性能指标，同时考虑模型训练和预测的时间作为资源消耗指标。
特定问题的遗传操作：我们可以针对SVM参数的特性来定制交叉和变异操作。例如，对于C和gamma参数，我们可以设计特定的变异策略来探索更广泛的参数空间。
并行计算：鉴于遗传算法中的种群可以独立评估，我们可以利用并行计算来加速适应度的评估过程。
早期停止机制：为了避免过度计算，我们可以设定一个早期停止机制，比如在连续几代中适应度没有显著提升时停止算法。

示例代码修改

下面是针对这个具体场景修改后的Python代码示例：

import numpy as np
from sklearn import svm
from sklearn.model_selection import cross_val_score
import time

# 模拟SVM模型评估
def evaluate_svm(parameters, X, y):
    model = svm.SVC(C=parameters[0], gamma=parameters[1])
    start_time = time.time()
    scores = cross_val_score(model, X, y, cv=5)
    elapsed_time = time.time() - start_time
    accuracy = np.mean(scores)
    resource_consumption = elapsed_time
    return accuracy, resource_consumption

# 修改后的适应度函数
def fitness_modified(accuracy, resource_consumption):
    return accuracy / resource_consumption  # 可根据需要调整适应度计算公式

# 略去种群初始化、选择、交叉和变异函数

# 遗传算法主函数修改
def genetic_algorithm_modified(pop_size, param_size, num_generations, X, y):
    population = initialize_population(pop_size, param_size)
    for generation in range(num_generations):
        fitnesses = []
        for individual in population:
            accuracy, resource_consumption = evaluate_svm(individual, X, y)
            fitnesses.append(fitness_modified(accuracy, resource_consumption))
        # 略去选择、交叉和变异步骤
    return population

# 示例数据集
# X, y = 加载您的数据集

# 参数设置
pop_size = 10
param_size = 2  # SVM的两个参数
num_generations = 10

# 运行遗传算法
optimized_population = genetic_algorithm_modified(pop_size, param_size, num_generations, X, y)
print("Optimized Parameters:\n", optimized_population)

在这个修改后的版本中，我们专注于优化SVM的参数，并采用了更加精确的评估和适应度计算方法。这些改进有助于更有效地应用遗传算法于实际的机器学习参数优化问题。

七、进一步优化遗传算法

1. 高级技巧与实践建议

多目标优化：
- 在机器学习中，我们经常需要同时考虑多个目标，如准确度、模型复杂度、运行时间等。
- 遗传算法可以通过非支配排序（如NSGA-II）来优化多个目标。
超参数调整：
- 遗传算法的效果很大程度上取决于其超参数，如种群大小、交叉率、变异率等。
- 通过实验和调整这些参数，可以显著提高算法的性能。
特征选择：
- 在某些机器学习问题中，除了优化模型参数外，还可以使用遗传算法进行特征选择。
- 通过优化特征子集来提高模型的性能和泛化能力。
与其他优化算法结合：
- 遗传算法可以与其他优化技术如梯度下降、贝叶斯优化等结合使用。
- 这种混合方法可以充分利用各自算法的优点，提高整体的优化效率。
并行化和分布式计算：
- 鉴于遗传算法的种群可以独立评估，它很适合进行并行化和分布式计算。
- 使用并行计算可以显著加快大规模问题的求解速度。

2.示例：进阶版遗传算法的Python实现

这里，我将提供一个更进阶的遗传算法实现示例，展示上述技巧的部分应用。

import numpy as np
from sklearn import datasets, svm
from sklearn.model_selection import cross_val_score
import time
from scipy.stats import rankdata

# 加载数据集
X, y = datasets.load_iris(return_X_y=True)

# 评估函数：SVM模型的交叉验证性能
def evaluate_svm(parameters):
    model = svm.SVC(C=parameters[0], gamma=parameters[1])
    scores = cross_val_score(model, X, y, cv=5)
    return np.mean(scores)

# 遗传算法的适应度函数：调整以适应多目标优化
def fitness(accuracy, time_consumed):
    # 这里可以根据实际需求调整多目标优化的权衡
    return accuracy - time_consumed

# 略去种群初始化、选择、交叉和变异函数

# 进阶版遗传算法主函数
def advanced_genetic_algorithm(pop_size, param_size, num_generations):
    population = initialize_population(pop_size, param_size)
    for generation in range(num_generations):
        fitnesses = []
        for individual in population:
            start_time = time.time()
            accuracy = evaluate_svm(individual)
            time_consumed = time.time() - start_time
            fitnesses.append(fitness(accuracy, time_consumed))
        # 略去选择、交叉和变异步骤
    return population

# 参数设置
pop_size = 20
param_size = 2
num_generations = 20

# 运行进阶版遗传算法
optimized_population = advanced_genetic_algorithm(pop_size, param_size, num_generations)
print("Optimized Parameters:\n", optimized_population)