Redis的实现三：c语言实现平衡二叉树，通过平衡二叉树实现排序集-Toy模板网

这篇具有很好参考价值的文章主要介绍了Redis的实现三：c语言实现平衡二叉树，通过平衡二叉树实现排序集。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

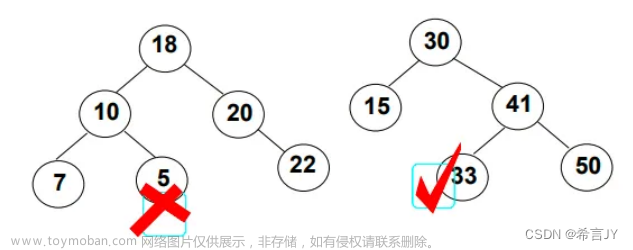
概况：Redis中的排序集数据结构是相当复杂的独特而有用的东西。它不仅提供了顺序排序数据的能力，而且具有按排名查询有序数据的独特特性。

Redis中的排序集

（Sorted Set）是一种特殊的数据结构，它结合了集合（Set）和有序列表（List）的特点。在Redis中，每个成员都有一个分数（score），分数可以是整数或浮点数。根据分数对成员进行排序，分数较低的成员排在前面，分数较高的成员排在后面。

以下是Redis中排序集的一些基本操作：

ZADD：向排序集中添加一个或多个成员，或者更新已存在成员的分数。
ZREM：从排序集中移除一个或多个成员。
ZRANGE：按照分数范围返回排序集中的成员。
ZREVRANGE：按照分数范围逆序返回排序集中的成员。
ZCOUNT：返回排序集中指定分数范围内的成员数量。
ZINCRBY：将指定成员的分数增加指定的值。
ZRANK：返回指定成员在排序集中的排名。
ZREVRANK：返回指定成员在排序集中的排名（逆序）。
ZSCORE：返回指定成员的分数。
ZDIFF、ZINTER、ZUNION：合并多个排序集并返回结果。

实际上真正的Redis项目使用的是skiplist，跳表在一定程度上可以替代平衡二叉树

c语言实现平衡二叉树

第一步：定义结构体

typedef struct Node {
    int data;
    struct Node *left;
    struct Node *right;
    int height;
} Node;

左节点，右节点，深度，数据

第二步：定义比较算法

int max(int a, int b) {
    return (a > b) ? a : b;
}

这个很简单的算法，就是单纯的比较两个数，取其中最大的。

第三步：创建节点

Node* createNode(int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    newNode->height = 1;
    return newNode;
}

第四步：得到高度

int getHeight(Node* node) {
    if (node == NULL) {
        return 0;
    }
    return node->height;
}

每个节点里面都包含了高度，这个属性。

第五步：计算平衡因子

int getBalance(Node* node) {
    if (node == NULL) {
        return 0;
    }
    return getHeight(node->left) - getHeight(node->right);
}

如果平衡因子为0，则表示该节点的左右子树高度相等，因此它是平衡的。如果getHeight(node->left) - getHeight(node->right)小于0，则表示左子树比右子树高，需要向左旋转操作来恢复平衡。如果getHeight(node->left) - getHeight(node->right)大于0，则表示右子树比左子树高，需要向右旋转操作来恢复平衡。

第六步：左旋函数

Node* leftRotate(Node* x) {
    Node* y = x->right;
    Node* T2 = y->left;

    y->left = x;
    x->right = T2;

    x->height = max(getHeight(x->left), getHeight(x->right)) + 1;
    y->height = max(getHeight(y->left), getHeight(y->right)) + 1;

    return y;
}

Redis的实现三：c语言实现平衡二叉树，通过平衡二叉树实现排序集,redis,数据库

第七步：右旋函数

Node* rightRotate(Node* y) {
    Node* x = y->left;
    Node* T2 = x->right;

    x->right = y;
    y->left = T2;

    y->height = max(getHeight(y->left), getHeight(y->right)) + 1;
    x->height = max(getHeight(x->left), getHeight(x->right)) + 1;

    return x;
}

这里就不过多讲解了。和左旋一样，画个图就明白了。

第八步：插入函数

Node* insert(Node* node, int data) {
    if (node == NULL) {
        return createNode(data);
    }

    if (data < node->data) {
        node->left = insert(node->left, data);
    } else if (data > node->data) {
        node->right = insert(node->right, data);
    } else {
        return node;
    }

    node->height = 1 + max(getHeight(node->left), getHeight(node->right));

    int balance = getBalance(node);

    if (balance > 1 && data < node->left->data) {
        return rightRotate(node);
    }

    if (balance < -1 && data > node->right->data) {
        return leftRotate(node);
    }

    if (balance > 1 && data > node->left->data) {
        node->left = leftRotate(node->left);
        return rightRotate(node);
    }

    if (balance < -1 && data < node->right->data) {
        node->right = rightRotate(node->right);
        return leftRotate(node);
    }

    return node;
}

这里面大多都运用到了递归，兄弟们可以先了解递归再来看这个。

第九步：遍历函数

void inorderTraversal(Node* root) {
    if (root != NULL) {
        inorderTraversal(root->left);
        printf("%d ", root->data);
        inorderTraversal(root->right);
    }
}

第十步：测试看结果

Redis的实现三：c语言实现平衡二叉树，通过平衡二叉树实现排序集,redis,数据库文章来源地址https://www.toymoban.com/news/detail-794063.html

完整代码

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int data;
    struct Node *left;
    struct Node *right;
    int height;
} Node;

int max(int a, int b) {
    return (a > b) ? a : b;
}

Node* createNode(int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    newNode->height = 1;
    return newNode;
}

int getHeight(Node* node) {
    if (node == NULL) {
        return 0;
    }
    return node->height;
}

int getBalance(Node* node) {
    if (node == NULL) {
        return 0;
    }
    return getHeight(node->left) - getHeight(node->right);
}

Node* rightRotate(Node* y) {
    Node* x = y->left;
    Node* T2 = x->right;

    x->right = y;
    y->left = T2;

    y->height = max(getHeight(y->left), getHeight(y->right)) + 1;
    x->height = max(getHeight(x->left), getHeight(x->right)) + 1;

    return x;
}

Node* leftRotate(Node* x) {
    Node* y = x->right;
    Node* T2 = y->left;

    y->left = x;
    x->right = T2;

    x->height = max(getHeight(x->left), getHeight(x->right)) + 1;
    y->height = max(getHeight(y->left), getHeight(y->right)) + 1;

    return y;
}

Node* insert(Node* node, int data) {
    if (node == NULL) {
        return createNode(data);
    }

    if (data < node->data) {
        node->left = insert(node->left, data);
    } else if (data > node->data) {
        node->right = insert(node->right, data);
    } else {
        return node;
    }

    node->height = 1 + max(getHeight(node->left), getHeight(node->right));

    int balance = getBalance(node);

    if (balance > 1 && data < node->left->data) {
        return rightRotate(node);
    }

    if (balance < -1 && data > node->right->data) {
        return leftRotate(node);
    }

    if (balance > 1 && data > node->left->data) {
        node->left = leftRotate(node->left);
        return rightRotate(node);
    }

    if (balance < -1 && data < node->right->data) {
        node->right = rightRotate(node->right);
        return leftRotate(node);
    }

    return node;
}

void inorderTraversal(Node* root) {
    if (root != NULL) {
        inorderTraversal(root->left);
        printf("%d ", root->data);
        inorderTraversal(root->right);
    }
}

int main() {
    Node* root = NULL;
    root = insert(root, 70);
    root = insert(root, 20);
    root = insert(root, 30);
    root = insert(root, 40);
    root = insert(root, 50);
    root = insert(root, 25);

    printf("Inorder traversal of the constructed AVL tree is: ");
    inorderTraversal(root);

    return 0;
}

到了这里，关于Redis的实现三：c语言实现平衡二叉树，通过平衡二叉树实现排序集的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！