算法设计与分析 期末复习 北邮BUPT

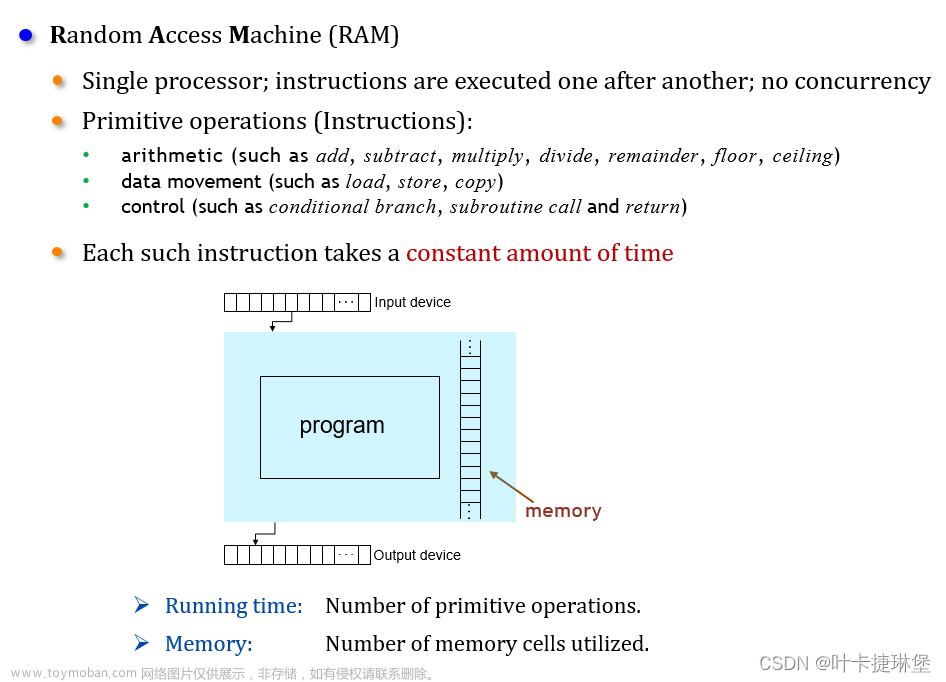
以下内容以“算法设计与分析-2022”王晓茹老师的ppt为大纲
问题、要求也均为老师课堂上的口述要求和ppt上的要求

1 算法复杂性分析和渐进性原理

1.1 算法复杂性的概念

• 渐进上界、渐进下界
  
• 证明 O ( f ( n ) ) + O ( g ( n ) ) = O ( m a x { f ( n ) , g ( n ) } ) O(f(n))+O(g(n)) = O(max\{f(n),g(n)\}) O(f(n))+O(g(n))=O(max{f(n),g(n)})
  
  （最后一行注意一下）

1.2 用特征方程解递归方程的通解

• ppt作业题
  
• 考试题
  
• ppt上的特殊情况（有两个特征根相等）
  

2 分治

2.1 快速排序

注意1：如何解决退化？（参考另一个博主的内容）
快速排序的优化

• 三数取中法（下方黄色字体“区分2”有详细代码）
• 当待排序序列的长度分割到一定大小后，使用插入排序
• 在一次分割结束后，把与key相等的元素聚在一起，继续下次分割时，不用再对与key相等元素分割

注意2：如何设计稳定排序？

• 插入排序
  利用有序表的插入操作进行排序（有序表的插入: 将一个记录插入到已排好序的有序表中，从而得到一个新的有序表。）
• 冒泡排序
  实现将n个数从小到大排序，两两比较，将最大的数放右边，一趟比较完后最右边的数即为最大数，然后n-1个数继续两两比较，将最大的数放在最右边，这是第二趟，共需要进行n-1趟。
• 合并排序
  实现一组数从小到大排序，核心即拆合，先将这组数拆成两两一组，按从小到大排序好，即有序，再将各个数组两两合并。

区分1：挖坑法与hoare法的区别

• 下方主代码为挖坑法（思路：取最左或最右边的元素为key，假设把这个位置“挖空”，让最右边的q向左走，直到遇到比key小的数，将其放到key的位置，自己的位置变“空”。直到pq相遇，那么这个位置就是最终的坑位，再将key填入这个坑位，就完成了一趟排序。）
• 另一种hoare方法见“线性时间选择”中的partition，区别在于，挖坑法进行一趟排序的时候key需要被保存，因为最开始就被a[j]给替代了；而hoare法则是key一直被保留在第一个，进行一趟排序的过程中a[i]和a[j]不断交换，最后退出while循环后进行a[key]和a[i]的交换。

区分2：基准值的三种选取

• 固定位置选择（以第一个元素为例）

int Normal(int a[],int low,int high)  
{  
    return a[low];  
}  

• 随机选择

int Random(int a[],int low,int high)  
{  
    //产生枢轴的位置
    srand((unsigned)time(NULL));  
    int temp = rand()%(high - low) + low;  
    //若要生成 a 与 b 之间的随机实数，应使用：rand()*(b-a)+a
    //把枢轴位置的元素和low位置元素互换，即可像普通的快排一样调用划分函数  
    swap(a[temp], a[low]);  
    return a[low];  
}  

• 三数取中

/*函数作用：取待排序序列中low、mid、high三个位置上数据，选取他们中间的那个数据作为枢轴*/  
int Median(int a[],int low,int high)  
{  
    int mid = low + (high - low) / 2;//计算数组中间的元素的下标  
    if (a[mid] > a[high])//目标: a[mid] <= a[high]  
    {  
        swap(a[mid], a[high]);  
    }  
    if (a[low] > a[high])//目标: a[low] <= a[high]  
    {  
        swap(a[low], a[high]);  
    }  
    if (a[mid] > a[low]) //目标: a[low] >= a[mid]  
    {  
        swap(a[mid], a[low]);  
    }  
    //此时，a[mid] <= a[low] <= a[high]  
    return a[low];  
    //low的位置上保存这三个位置中间的值，分割时可以直接使用low位置的元素作为枢轴，而不用改变分割函数了  
} 

考试题1：分析划分元素的选取对算法性能的影响？

• 快速排序算法的性能取决于划分的对称性。通过修改算法partition，可以设计出采用随机选择策略的快速排序算法。在快速排序算法的每一步中，当数组还没有被划分时，可以在a[p:r]中随机选出一个元素作为划分基准，这样可以使划分基准的选择是随机的，从而可以期望划分是较对称的。（来自ppt）
• 基准元素的选取对于快速排序的性能影响很大
  • 最好的情况是选取的基准元素是序列的中位数，这样划分以后左子序列和右子序列的大小就相同；
  • 如果选取的基准元素是最小值或最大值，那么划分以后左子序列和右子序列有一个几乎为空，这样算法的效率就退化为$n^2$。比如，原来的序列已经几乎是有序的，那么上述选取基准值的方法就不可靠了。
• 在对于序列没有任何先验假设的情况下，一个比较稳妥的方法是选取左边界值，中间值，右边界值的中位数作为基准元素。

考试题2：快速排序的基本思想

• 选取一个基准，一趟排序确定两个区间，一个区间全部比基准值小，另一个区间全部比基准值大，接着再选取一个基准值来进行排序，以此类推，最后得到一个有序的数列。

其他问题：快速排序的步骤

• 选取基准值，通过不同的方式挑选出基准值。
• 用分治的思想进行分割，通过该基准值在序列中的位置，将序列分成两个区间，在准值左边的区间里的数都比基准值小（默认以升序排序），在基准值右边的区间里的数都比基准值大。
• 递归调用快速排序的函数对两个区间再进行上两步操作，直到调用的区间为空或是只有一个数。

void quicksort(int a[10000], int left, int right)
{
    int i = left, j = right, pivotkey = a[left];
    if (left >= right) return;
    while (i < j)
    {
        while (i < j && a[j] >= pivotkey)//从右向左扫描
            j--;
        a[i] = a[j];//碰到更小的数则停下来放到基准位置左边（基准位置会变）
        while (i < j && a[i] <= pivotkey)//从左向右扫描
            i++;
        a[j] = a[i];//碰到更大的数则停下来放到基准位置右边
    }
    a[i] = pivotkey;
    quicksort(a, left, i - 1);//对基准位置以左的区间做子任务
    quicksort(a, i + 1, right);//对基准位置以右的区间做子任务
}

含有partition、三数取中的版本（另一个博主的代码）
partion+qsort

//交换子表的记录，使枢轴记录到位，并返回枢轴所在的位置
int Partition(int a[], int low, int high){
 
	/*三数中值分割法*/
	int mid = low + (high - low) / 2;//计算数组中间的元素的下标  
    if (a[mid] > a[high])//目标: a[mid] <= a[high]  
    {  
        swap(a[mid], a[high]);  
    }  
    if (a[low] > a[high])//目标: a[low] <= a[high]  
    {  
        swap(a[low], a[high]);  
    }  
    if (a[mid] > a[low]) //目标: a[low] >= a[mid]  
    {  
        swap(a[mid], a[low]);  
    }  
	int pivotkey = a[low];
	
	/*随机基准元
	int randomIndex = rand() % (high - low) + low;//取数组中随机下标
	swap(array, randomIndex, low);                //与第一个数交换
	int pivotkey = array[low];
	*/
 
	int i = low, j = high;
	while(i < j) //从表的两端交替向中间扫描,当没有相遇
	{
		while (a[j] >= pivotkey && i<j){
			j--;
		}
		while (a[i] <= pivotkey && i<j){
			i++;
		}
		if (i < j)
		{
			swap(a, i, j);
		}	
	}
	//最终将基准数归位
	swap(a, low, i);
	return i;              //返回枢轴所在的位置
}
void QSort(int array[], int low, int high){
	int pivot;
	if (low < high)
	{
		pivot = Partition(array, low, high);//算出枢轴值
		QSort(array, low, pivot - 1);       //对低子表递归排序
		QSort(array, pivot + 1, high);      //对高子表递归排序
	}
}
//对array做快速排序
void QuickSort(int array[], int n){
	QSort(array, 0, n - 1);
}

2.2 合并排序

注意1：合并过程较为复杂，对于分解和合并的函数要掌握好
注意2：合并排序的空间复杂度和辅助空间

• 临时的数组和递归时压入栈的数据占用的空间：n + logn；所以空间复杂度为: $O(n)$

注意3：合并排序的两种方式（消除分解与否？）

• 方法一基本思想：将待排序元素分成大小大致相同的2个子集合，分别对2个子集合进行排序，最终将排好序的子集合并成为所要求的排好序的集合。
• 方法二具体过程：（算法mergeSort的递归过程可以消去）
  • 首先将长度为1的n个数组相邻元素两两合并，构成了长度为2的n/2个数组，合并时用比较算法对这每个子数组中元素进行排序；
  • 再将这些长度为2的n/2个数组两两合并，构成了长度为4的n/4的子数组，合并时用比较算法对每个子数组中元素进行排序。
  • 继续，直到形成长度为n，子数组个数=1的整个数组为止。

注意4：合并排序算法的稳定性

• 合并排序是把序列递归地分成短序列，递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换)，然后把各个有序的段序列合并成一个有序的长序列，不断合并直到原序列全部排好序。
• 在1个或2个元素的序列中，1个元素不会交换，2个元素如果大小相等也没有人故意交换，这不会破坏稳定性。
• 那么，在短的有序序列合并的过程中，稳定是是否受到破坏？没有，合并过程中可以保证如果两个当前元素相等，处在前面的序列的元素会被保存在结果序列的前面，这样就保证了稳定性。

注意5：时间复杂度

void merge(int a[10000], int left, int right)
{
    int i = left, j = (left + right) / 2 + 1, point = 0;
    int b[10000];
    memset(b, 0, sizeof(b));
    while (i <= (left + right) / 2 && j <= right)//在两个对半的区间进行合并处理
    {
        if (a[i] < a[j])//左侧区间的数字更小
            b[point++] = a[i++];//同时进行临时数组的更新和指针的移动
        else//右侧区间的数字更小（或者相等）
            b[point++] = a[j++];//同时进行临时数组的更新和指针的移动
    }
    while (i <= (left + right) / 2)//左半区间如果还有剩下的则放入临时数组b中
        b[point++] = a[i++];
    while (j <= right)//右半区间同理，此二循环只有一个循环会被执行
        b[point++] = a[j++];
    point = 0;
    for (j = left; j <= right; j++)//临时数组中的内容复制回原数组中
        a[j] = b[point++];
}
void mergesort(int a[10000], int left, int right)
{
    if (left >= right) return;//当前区间长度小于等于1结束递归
    int mid = (left + right) / 2;
    mergesort(a, left, mid);//划分出左半区间做子任务
    mergesort(a, mid + 1, right);//划分出右半区间做子任务
    merge(a, left, right);//子任务的关键是合并
}

2.3 线性时间选择

• 题目：
  • 选择问题：给定线性序集中n个元素和一个整数k，1≤k≤n，要求找出这n个元素中第k小的元素
  • 线性时间选择问题：如果能在线性时间内找到一个划分基准，使得按这个基准所划分出的2个子数组的长度都至少为原数组长度的ε倍(0<ε<1是某个正常数)，那么就可以在最坏情况下用$O(n)$时间完成选择任务。
    • 例如，若ε=9/10，算法递归调用所产生的子数组的长度至少缩短1/10。所以，在最坏情况下，算法所需的计算时间T(n)满足递归式$T(n)\le T(9n/10)+O(n)$ 。
      由此可得$T(n)=O(n)$。
• 考试题目：
  （1）（5分）说明用分治法设计相关算法的过程；(2)(3)略
  
  • Pivot/划分基准的选择：
    i)将n个输入元素划分成 n/5 个组，每组5个元素，只可能有一个组不是5个元素。用任意一种排序算法，将每组中的元素排好序，并取出每组的中位数，共 n/5 个。
    ii)递归调用select来找出这 n/5 个元素的中位数。如果 n/5 是偶数，就找它的2个中位数中较大的一个。
    iii)以这个元素作为划分基准。
  • 设所有元素互不相同。在这种情况下，找出的基准x至少比3(n-5)/10个元素大，因为在每一组中有2个元素小于本组的中位数，而n/5个中位数中又有(n-5)/10个小于基准x。同理，基准x也至少比3(n-5)/10个元素小。而当n≥75时，3(n-5)/10≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4。
    （需要-5的原因：要考虑n不是5的倍数的情况）
• 时间复杂度分析
  （考试题目）对该算法最坏情况下的时间复杂度（比较次数）进行分析，注意尽可能给出最坏情况下的分析时相关的准确比较次数。
  • 最坏情况时间复杂度
    若ε=9/10，算法递归调用所产生的子数组的长度至少缩短1/10。所以，在最坏情况下，算法所需的计算时间T(n)满足递归式T(n)≤T(9n/10)+O(n) 。由此可得T(n)=O(n)。
  • 代码时间复杂度
    
    $T(n)=O(n)$

注意1：partition函数（选择第n小），存在退化
注意2：ppt代码未写出来，需要补全

#include<iostream>
#include<cstdlib>
#include<cstdio>
using namespace std;

void bubbleSort(int a[],int p,int r)
{
    for (int i = p; i < r; i++)
    {
        for (int j = i + 1; j <= r; j++)
        {
            if (a[j] < a[i])
                swap(a[i], a[j]);
        }
    }
}
int Partition(int a[], int p, int r, int val)//单趟排序（hoare法）
{
    int pos = p, t = a[pos];
    int i = p, j = r;
    while (i < j)
    {
        while (i < j && a[j] >= t)//从右向左扫描
            j--;
        while (i < j && a[i] <= t)//从左向右扫描
            i++;
        swap(a[i], a[j]);
    }
    swap(a[pos], a[i]);
    return j;
}
int Select(int a[], int p, int r, int k)
{
    if (r - p < 75)
    {
        bubbleSort(a, p, r);//用某个简单排序算法对数组a[p:r]排序;
        return a[p + k - 1];
    }
    //找中位数的中位数，r-p-4即上面所说的n-5
    for (int i = 0; i <= (r - p - 4) / 5; i++)//把每个组的中位数交换到区间[p,p+(r-p-4)/4]
    {
        //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
        bubbleSort(a, p + 5 * i, p + 5 * i + 4);
        swap(a[p + i], a[p + 5 * i + 2]);//交换每组中的中位数到前面
    }
    //找所有中位数的中位数，r-p-4即上面所说的n-5
    int x = Select(a, p, p + (r - p - 4) / 5, (r - p - 4) / 10);
    /* (r-p+1)/10 = (p+(r+p-4)/5-p+1)/2 */
    //以x为基准做一次快排
    int i = Partition(a, p, r, x), j = i - p + 1;
    //判断k属于哪个部分
    if (k <= j) return Select(a, p, i, k);
    else return Select(a, i + 1, r, k - j);
}
int main()
{
    int x;
    //数组a存了0-79
    int a[80]= {3,1,7,6,5,9,8,2,0,4,13,11,17,16,15,19,18,12,10,14,23,21,27,26,25,29,28,22,20,24,33,31,37,36,35,39,38,32,30,34,43,41,47,46,45,49,48,42,40,44,53,51,57,56,55,59,58,52,50,54,63,61,67,66,65,69,68,62,60,64,73,71,77,76,75,79,78,72,70,74};
    cin >> x;
    cout << "第" << x << "小的数是" << Select(a, 0, 79, x) << endl;
}

3 动态规划

• 要求：
  • 分析是否满足最优子结构，证明方法是用反证法来进行证明的，子问题的最优解和原问题的最优解在这一部分是重叠的。
  • 写出递推式
  • 自底向上求解，避免重复
  • 构造最优解

3.1 矩阵连乘

• 问题描述：
  • 给定n个矩阵{$A_1$, $A_2$, …, $A_n$}，其中Ai与$A_{i+1}$是可乘的，i=1,2,…,n-1。
  • 考察这n个矩阵的连乘积$A_1{A}_2...A_n$
  • 由于矩阵乘法满足结合律，所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。
  • 若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号，则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积
    
• 递归关系式
  
  其中k的位置只有j-i种可能
• 代码

#include <iostream>
using namespace std;
int A[100][100], s[100][100], p[100];
void traceback(int i, int j)
{
    if (i == j) return;
    traceback(i, s[i][j]);
    traceback(s[i][j] + 1, j);
    cout << i << ' ' << s[i][j] << ' ';
    cout << s[i][j] + 1 << ' ' << j << "    ";
    cout << p[i] << ' ' << p[s[i][j]] << ' ';
    cout << p[s[i][j] + 1] << ' ' << p[j] << endl;
}
int main() {
    int n;
    int i, j, r, k;
    cin >> n;
    for (i = 0; i <= n; i++)
        cin >> p[i];
    for (i = 1; i <= n; i++)
        A[i][i] = 0;
    for (r = 2; r <= n; r++)
        for (i = 1; i <= n - r + 1; i++)//不算第n行
        {
            j = i + r - 1; //比如最开始算的是（1,2）
            A[i][j] = A[i + 1][j] + p[i - 1] * p[i] * p[j];
            s[i][j] = i;
            for (k = i + 1; k <= j; k++)
                if (A[i][k] + A[k + 1][j] + p[i - 1] * p[k] * p[j] <= A[i][j])
                {
                    A[i][j] = A[i][k] + A[k + 1][j] + p[i - 1] * p[k] * p[j];
                    s[i][j] = k;
                }
        }
    traceback(1, n);
    return 0;
}
/*
6
30 35 15 5 10 20 25
 */

3.2 最长公共子序列

• 问题描述：给定两个序列 X = { x 1 , x 2 , … . . , x m } X=\{ x_1, x_2, ….., x_m\} X={x1​,x2​,…..,xm​}， Y = { y 1 , y 2 , … … , y n } Y=\{y_1, y_2, ……, y_n\} Y={y1​,y2​,……,yn​}，找出X和Y的一个最长公共子序列。
• 最优子结构性质：
  • 设序列 X = { x 1 , x 2 , … . . , x m } X=\{ x_1, x_2, ….., x_m\} X={x1​,x2​,…..,xm​}和 Y = { y 1 , y 2 , … … , y n } Y=\{y_1, y_2, ……, y_n\} Y={y1​,y2​,……,yn​}的最长公共子序列为 Z = { z 1 , z 2 , … … , z k } Z=\{z_1, z_2, ……, z_k\} Z={z1​,z2​,……,zk​}，则
  1. 若$x_m=y_n$，则$z_k=x_m=y_n$，且$Z_{k-1}$是$X_{m-1}$和$Y_{n-1}$的最长公共子序列。
  2. 若$x_m\ne y_n$且$z_k\ne x_m$，则$Z_k$是$X_{m-1}$和$Y_n$的最长公共子序列。
  3. 若$x_m\ne y_n$且$z_k\ne y_n$，则$Z_k$是$X_n$和$Y_{n-1}$的最长公共子序列。
• 子问题的递归结构
  
• 代码

void LCSLength(int m, int n, char x[100], char y[100], int c[100][100], int b[100][100])//求长度
{
    int i, j;
    for (i = 1; i <= m; i++) c[i][0] = 0;
    for (i = 1; i <= n; i++) c[0][i] = 0;
    c[0][0] = 0;
    for (i = 1; i <= m; i++)
        for (j = 1; j <= n; j++)
        {
            if (x[i] == y[j])
            {
                c[i][j] = c[i - 1][j - 1] + 1; b[i][j] = 1;
            }
            else if (c[i - 1][j] >= c[i][j - 1])
            {
                c[i][j] = c[i - 1][j]; b[i][j] = 2;
            }
            else
            {
                c[i][j] = c[i][j - 1]; b[i][j] = 3;
            }
        }
}

void LCS(int i, int j, char x[100], int b[100][100])//构造公共子序列
{
      if (i == 0 || j == 0) return;
      if (b[i][j] == 1)
      {
          LCS(i - 1, j - 1, x, b);
          cout << x[i];
      }
      else if (b[i][j] == 2)
          LCS(i - 1, j, x, b);
      else LCS(i, j - 1, x, b);
}

3.3 最大字段和

• 问题描述
  
  
• 数组b[j]：表示以下标j结束的最大子数组的和的值。
• 思考：以下标1为结束的数组{1,-5}的最大子数组和是什么？（注意：这里指的最大子数组必须以下标1(或者说j)结束）
• 答案：
  • 如果以下标0结束的最大子数组的和为正数，那么b[1]就是b[0]+a[1]；
  • 如果如果以下标0结束的最大子数组的和为负数，那么b[1]就是a[1]。所以b[1]=b[0]+a[1]=-4。
• 递归关系式
  
• 代码（原始版本）

int maxSum(int n, int a[100])
{
    int sum = 0, b = 0;
    for (int i = 1; i <= n; i++)
    {
        if (b > 0) b += a[i];
        else b = a[i];
        if (b > sum) sum = b;
    }
    return sum;
}

上面的代码中，也对空间复杂度做了小小的优化，b[]这个数组没有必要开，原因是b[j]只和b[j-1]有关系，所以用一个变量b即可。从代码中也可以看到，只有一层循环i，用来枚举结束的下标。

• 代码（构造了最优解的版本）

int maxSum(int n, int a[100])
{
    int sum = 0, b = 0;
    for (int i = 1; i <= n; i++)
    {
        if (b > 0) b += a[i];
        else
        {
            b = a[i];
            tempbegin = i;
        }
        if (b > bestsum)
        {
            bestsum = b;
            bestbegin = tempbegin;
            bestend = i;
        }
    }
    return sum;
}

• ppt上的代码
  

int getmax(int a[100], int n)
{
    int sum = 0, sumMin = 0, max = a[0];
    for (int i = 0; i < n; i++)
    {
        if (sumMin > sum)
            sumMin = sum;
        sum = sum + a[i];
        if (sum - sumMin > Max)
            Max = sum - sumMin;
    }
    return Max;

3.4 01背包问题（优化问题不考）

• 递推关系式
  
• 代码

#include<iostream>
#include<iomanip>
using namespace std;
int n, c;
int m[100][100], weight[100], value[100], x[100];
void Traceback()//构造最优解
{
    memset(x, 0, sizeof(x));
    for (int i = 1; i < n; i++)
        if (m[i][c] == m[i + 1][c])
            x[i] = 0;
        else
        {
            x[i] = 1;
            c -= weight[i];
        }
    if (m[n][c] != 0)
        x[n] = 1;
    else m[n][c] = 0;
}
int main()
{
    int i, j;
    cin >> n >> c;//n件物品 c的容量
    for (i = 1; i <= n; i++)
        cin >> weight[i] >> value[i];
    for (j = 0; j <= c; j++)//注意从0开始
        if (j < weight[n]) m[n][j] = 0;  //不要忘记对m赋初始值
        else m[n][j] = value[n];
    for (i = n - 1; i >= 1; i--)
        for (j = 0; j <= c; j++)
        {
            if (j >= weight[i])
            {
                if (m[i + 1][j] > m[i + 1][j - weight[i]] + value[i])
                    m[i][j] = m[i + 1][j];
                else
                    m[i][j] = m[i + 1][j - weight[i]] + value[i];
            }
            else m[i][j] = m[i + 1][j];
        }
    cout << m[1][c] << endl;
    for (i = 1; i <= n; i++)
    {
        for (j = 0; j <= c; j++)
            cout << setw(3) << m[i][j];
        cout << endl;
    }
    Traceback();
    for (i = 1; i <= n; i++)
        cout << setw(3) << x[i];
    cout << endl;
}

4 贪心

• 贪心和动态规划的使用范围：
  • 如果问题的最优解包含两个（或更多）子问题的最优解，且子问题多有重叠，则考虑使用动态规划算法。
  • 如果问题经过贪心选择后，只剩下一个子问题，且具有最优子结构，那么可以使用贪心算法。
• 注意1：证明当前问题用贪心法可以得到最优解（包括最优子结构+贪心选择的证明）
• 注意2：复习复杂性（要包括排序的时间复杂度）

4.1 活动安排

• 问题描述

设有n个活动的集合E＝{1，2，…，n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。
每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi，且si＜fi。如果选择了活动i，则它在半开时间区间[si ，fi)内占用资源。若区间[si ，fi)与区间[sj，fj)不相交，则称活动i与活动j是相容的。当 si ≥ fj 或 sj ≥ fi时，活动i与活动j相容。 活动安排问题就是在所给的活动集合中选出最大的相容活动子集合。

• 贪心选择
  
• 最优子结构
  
  
  
• 贪心策略和时间复杂度
  
• 过程
  • 将各个活动按照活动结束时间fi排序，且f1<=f2<=f3…
  • 选择结束时间最早的活动1
  • 从2开始按顺序比较各个活动，选择第一个与活动1相容的活动i
  • 从i+1开始按顺序考察各个活动，选择第一个与活动 i 相容的活动 j
• 代码

void greedy(int n, int s[100], int f[100], bool a[100])
{
    A[1] = true;
    int j = 1;
    for (int i = 2; i <= n; i++){
        if (s[i] >= f[j])
        {
            A[i] = true;
            j = i;
        }
        else A[i] = false;
}

4.2 背包问题

• 问题描述

与01背包问题类似，所不同的是在选择物品i装入背包时，可以选择物品i的一部分，而不一定要全部装入背包，1<=i<=n。

• 背包问题和01背包问题的区分
  • 与0-1背包问题类似，不同的是在选择物品i装入背包时，可以选择物品的一部分，即0<=$x_i$<=1
  • 这两类问题极为相似，都具有最优子结构性质：对n种物品E={1, 2, 3, … , n}，其最优解为{$x_1$, $x_2$, $x_3$, … , $x_{n-1}$, $x_n$}。则$X_j$=X-{$x_j$}={$x_1$, $x_2$, … , $x_{j-1}$, $x_{j+1}$, … , $x_{n-1}$, $x_n$}是n-1个物品的子问题E’={1, 2, … , j-1, j+1, … , n-1, n}的最优解——去掉第j个物品。
  • 这两类问题都具有最优子结构性质；但是背包问题具有贪心选择性质，可以用贪心算法求解；而0-1背包问题不能用贪心算法求解。
• 背包问题有三种看似合理的贪心策略
  • 选择价值最大的物品
  • 选择重量最轻的物品
  • 选择单位重量价值最大的物品
• 01背包问题不能用贪心算法的原因
  
• 考试题：
  (1) （4分）给出此优化问题的整数规划数学公式，即问题的形式化描述。
  
  (2) （4分）给出该问题贪心算法求解的贪心策略。
  
  
  (3) （6分）基于C/C++/Java/Python等高级编程语言写出贪心算法的伪代码。
  见下方代码
  (4) （3分）分析(3)中给出的贪心算法的时间复杂性。
  $O(nlogn)$
  (5) （3分）给定4种物品重量分别为{10, 40, 55, 20} 价值分别为{20, 120, 55, 100}, 背包容量是100，求背包的最大价值以及对应的放入背包的物品重量。
• 过程
  • 计算每种物品的单位重量的价值
  • 排序，装入背包；
  • 尾部处理
• 代码

void package(int n, float M, float v[], float w[], float x[])
{
    sort(n, v, w);//对n个物品计算单位重量的价值v[i]/w[i]，从大到小排序
    int i;
    for (i = 1; i <= n; i++)
        x[i] = 0;
    float c = M;
    for (i = 1; i <= n; i++)
    {
        if (w[i] > c) break;//物品i的重量超出当前可用背包容量，算法停止
        x[i] = 1;
        c -= w[i];
    }
    if (i <= n && c > 0) x[i] = c / w[i];
    //如果背包还有剩余容量（C>0），将剩余容量分配给物品i
}

4.3 最优装载（另一个老师复习ppt上的重点内容）

• 问题描述

有n个集装箱要装上一艘载重量为c的轮船。其中集装箱i的重量为Wi。
最优装载问题要求确定在装载体积不受限制的情况下，将尽可能多的集装箱装上轮船—装载的集装箱数目极大化，且装入的总重量不超过c（装载重量受限）。

最优装载问题看作是0-1背包问题的1个特例：集装箱=物品，每种物品价值函数v[i]=1。

• 数学化形式
  
• 贪心策略
  
• 贪心选择
  设集装箱已按重量从小到大排序，{x1, x2, …, xn} 是最优装载问题的一个最优解。
  设k为最先装入箱中的最轻货物，即
  
  当问题有最优解（有可能是非贪心策略解）时，
  （1）当k=1，即最轻的第1个货物被装入，货物选择的放入顺序符合贪心策略， {x1, x2, …, xn} 是满足贪心选择性质的一个最优解
  （2）当k>1时，最轻的货物1没有被装入。
  按如下方式从{x1, x2, …, xn}构造出一个满足贪心策略的最优解{y1, y2, …,yk, …, yn}, y1=0：
  i) 对k, 其中1<k<n, yk=1**,取y1=1, yk=0**，将第1个货物放入，第k个货物拿出，即用第1个货物替换原方案中最轻的货物，而第1个货物比第k个货物更轻，即w1≤wk。
  ii) yi=xi, 1≤i≤n, i≠k, 其它货物是否被放入仍保持不变。
  新方案仍然满足容量约束条件：
  
• 最优子结构
  假设货物{1,2,…,n}已按重量从小到大排序。
  对原问题：待装货物为{1,2,…, n}、容量为C，{x1, x2, …, xn}是其满足贪心策略的1个最优解, 且x1=1。
  e.g. {x1, x2, …, xn}={1, 0, 1, 0, 1}，k=1
  则对子问题：待装货物为{2,…,n}、容量为C-w1， {x2, …, xn}是一个最优解, e.g. {x2, …, xn}={0, 1, 0, 1}
  e.g. {x2, …, xn}={0, 1, 0, 1}
• 代码

void loading(int x[], int w[], int c, int n)
{
    sort(w, t, n);
    for (int i = 1; i <= n; i++) x[i] = 0;
    for (int i = 1; i <= n && w[t[i]] <= c; i++)//t[i]存储的是物品标号（从小到大排列）
    {
        x[t[i]] = 1;
        c -= w[t[i]];
    }
}

4.4 哈弗曼编码

（此处贪心选择和最优子结构写的不全，参考ppt）

• 贪心选择
  设字符集C’={c | f©}，x和y是其中具有最小频率f(x)和f(y)的2个字符，则存在C’的最优前缀码，使x和y具有相同码长，且只有最后一位编码不相同。
  e.g. f: 1100, e:1101
  如果能证明上述命题，就说明构造算法是正确的——全局最优
• 最优子结构
  需要证明：
  给定字符集C和其对应的最优前缀码T，可以从中得到子问题C’ (C的子集)及其对应的最优前缀子树T‘
• 时间复杂度
  $T=O(nlogn)$
• 构建哈夫曼树的详细过程参考：哈夫曼树算法、示例
• 伪代码

void Huffman(PriorityQueue Q[ ], int n)
{
    //Let Q be the priority queue.
    Q = {initialize priority queue with frequencies of all symbol or message}
    for (i = 1; i < n; i++)
    { 
        create a new node z;
        /* be greedy here */
        x = extract_min(Q);
    	y = extract_min(Q);
    	Frequency(z) = Frequency(x) +Frequency(y);
        /* weight of a tree = sum of the frequencies of its leaves */
        Insert(z, Q);
    }
}

4.5 最小生成树（略）

4.6 单源最短路径

• 考试题：

（1）(5分)说明Dijkstra求解该问题的贪心策略，并给出求解过程。
每次从V-S中取出具有(只经过S中顶点)的最短特殊路长度dist[u]的顶点u，将u添加到S中，同时对数组dist作必要的修改。


（2）(6分)证明该贪心算法的正确性，即该贪心算法能够获得最优解（参考ppt）

A.贪心策略

在每步迭代时，从V-S中选择具有最短特殊路径dist[u]的顶点u，加入S

B.贪心选择

需证明对任意顶点u，从v开始、经过G中任意顶点到达u的全局最短路径的长度d(v, u) =从v开始、只经过S中顶点到达u的最短路径的长度dist(u)。
即：不存在另一条v到u的最短路径，该路径上某些节点x不在V-S中，且该路径的长度d(v,u) < dist[u]。

反证法
a.假设：
i.在迭代求解过程中，顶点u是遇到的第1个满足: d(v,u) < dist[u], 即 d(v,u)≠dist[u] 的顶点
ii.从v到u的全局最短路径上，第1个属于V-S的顶点为x

b.首先，因为u是第一个满足全局最短路径不完全在S集合中的顶点, 即d(v, u) < dist[u]

c.而x是在u之前遇到的顶点，x的最短路径完全在S中，即dist[x] = d(v, x)

d.对v到u的全局最短路径，有d(v, x) + distance(x, u) = d(v ,u) < dist[u]（根据假设）

e.由于distance(x, u) >0，因此dist[x] = d(v, x) ≤ d(v ,u) < dist[u]，即dist[x]< dist[u]

f.但是根据路径p构造方法，在下图所示情况下，u、x都在集合S之外，即u、x都属于V-S，但u被选中时，并没有选x，根据扩展S的原则——选dist最小的顶点加入S，说明此时dist[u] ≤ dist[x]

这与前面推出的dist[x]< dist[u]相矛盾

c.最优子结构

对顶点u，考察将u加到S之前和之后，**dist[u]**的变化，添加u之前的S称为老S，加入u之后的S称为新S。
要求：u加到S中后，dist[u]不增加。

对另外1个节点i，考察u的加入对**dist[i]**的影响：
1）假设添加u后, 出现1条从v到i的新路，该路径先由v经过老S中的顶点到达u，再从u经过一条直接边到达i
如果dist[u] + c[u][i] <原来的dist[i]，则算法用dist[u] + c[u][i] 替代dist[i]，得到新的dist[i]。否则， dist[i]不更新。

2）如果新路径如下图所示，先经过u，再回到S中的x，由x直接到达i。
x处于老的S中， 故dist[x]已经是最短路径，x比u先加入S，因此
dist[x] ≤dist[u] + d(u,x)
此时，从原v到i的最短路径dist[i]小于路径（v, u, x, i）的长度，因此算法更新dist[i]时不需要考虑该路径，u的加入对dist[i]无影响。

因此，无论算法中dist[u]的值是否变化，它总是关于当前顶点集合S的到顶点u的最短路径。
也就是说：对于加入u之前、之后的新老S所对应的2个子问题，算法执行过程保证了dist[u]始终是u的最优解

（3）(4分)分析所写算法的复杂性
用带权邻接矩阵表示具有n个顶点和e条边的带权有向图G(V, E)。
Dijkstra算法的主循环体需要$O(n)$时间。这个循环需要执行n-1次，所以完成循环需要$O(n^2)$时间。
算法的其余部分所需要时间不超过$O(n^2)$

• 代码

bool visited[MaxVerNum];//访问标记数组，用于遍历时的标记
//最短路径 - Dijkstra算法 参数：图G、源点v
void Dijkstra(Graph G, int v)
{
    //初始化：是否在S中、距离D、前驱结点标号Pr
    int n = G.vexnum;//n为图的顶点个数
    for (int i = 0; i < n; i++)
    {
        S[i] = false;
        D[i] = G.Edge[v][i];
        if (D[i] < INF)Pr[i] = v; //v与i连接，v为前驱
        else Pr[i] = -1;
    }
    S[v] = true;
    D[v] = 0;
    //初始化结束,求最短路径，并加入S集
    for (int i = 1; i < n; i++)
    {
        int min = INF;
        int temp;
        for (int w = 0; w < n; w++)
            if (!S[w] && D[w] < min) //某点temp未加入s集，且为当前最短路径
            {
                temp = w;
                min = D[w];
            }
        S[temp] = true;
        //更新从源点出发至其余点的最短路径 通过temp
        for (int w = 0; w < n; w++)
            if (!S[w] && D[temp] + G.Edge[temp][w] < D[w])
            {
                D[w] = D[temp] + G.Edge[temp][w];
                Pr[w] = temp;
            }
    }
}
//两次更新，对于每次更新都是两个条件+两个项的更新

5 回溯

• 回溯法的基本思想
  
  
• 子集树和排列树
  • 子集树
    • 当所给的问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间称为子集树。
    • 遍历子集树需$O(2^n)$计算时间
      
    • 伪代码

    void backtrack(int t)
    {
        if (t > n) output(x);
        else
            for (int i = 0; i <= 1; i++)
            {
                x[t] = i;
                if (legal(t)) backtrack(t + 1);
            }
    }
    

  • 排列树
    • 当所给的问题是确定n个元素满足某种性质的排列时，相应的解空间树成为排列树。
    • 遍历排列树需要$O(n!)$计算时间
      
    • 伪代码

    void backtrack(int t)
    {
        if (t > n) output(x);
    	else
    	    for (int i = t; i <= n; i++)
    	    {
    	        swap(x[t], x[i]);
    	        if (legal(t)) backtrack(t + 1);
    	        swap(x[t], x[i]);
    	    }
    } 
    

5.1 轮船装载问题

• 问题描述：
  有一批共n个集装箱要装上2艘载重量分别为c1和c2的轮船，其中集装箱i的重量为wi，且$\sum _n^{i=1}{w}_i\le c_1+c_2$
• 时间复杂度：
  由于bestx可能被更新$2^n$次，算法的时间复杂度为$O(2^n)$

注意1：子集树

void loading(int i)
{
    if (i > n)
    {
        for (int j = 1; j <= n; j++)
            cout << x[j] << ' ';
        cout << endl;
        if (cw > bestw)
        {
            for (int j = 1; j <= n; j++)
                bestx[j] = x[j];
            bestw = cw;
        }
        return;
    }
    //r -= w[i];
    if (cw + w[i] <= c)
    {
        x[i] = 1;
        cw += w[i];
        loading(i + 1);
        x[i] = 0;//无论进入下一层与否都会执行，这是更保险的位置
        cw -= w[i];
    }
    //if (cw + r > bestw)
    //{
        loading(i + 1);
    //}
    //r += w[i];
}

对于样例n=3, c1=50, w={20, 40, 40}

• 剪枝下的情况
  
• 未剪枝下的情况
  

5.2 旅行售货员问题

注意1：排列树文章来源地址https://www.toymoban.com/news/detail-794470.html

• 作业题（非ppt上代码）
• 函数说明：
  • inX：判断当前结点是否被访问过
  • TSPrecursion：回溯
• 伪代码：
  • 边界条件
    • 更新路径和最优解
    • 更新路径最优解
    • 路径和回溯
  • 循环递归
    • 可行性：剩余可选城市
    • 剪枝：加入当前城市会小于最短路径
      • 路径选中
      • 路径和选中
      • 递归下一层
      • 路径回溯
      • 路径和回溯
• 剪枝/约束条件
  • 1：如果当前正在考虑的顶点j与当前路径中的末端结点i没有边相连，即w[i, j]= ∞, 则不必搜索j所在分支
  • 2：如果B(i) ≥ bestw, 则停止搜索x[i]分支及其下面的层 ，
    其中，bestw代表到目前为止,在前面的搜索中，从其它已经搜索过的路径中，找到的最佳完整回路的权和（总长度）
• 时间复杂度：求排列问题。确认n个元素的满足某种性质的排列。其搜索树称为排列树，通常有n!个叶结点，因此遍历排列树需要时间为$O(n!)$
• 解空间树（包括剪枝）练习
  
  

bool inX(int i)//判断当前结点i是否被访问过
{
    for (int j = 0; j <= i - 1; j++)
        if (i == x[j]) return true;
    return false;
}
void TSPrecursion(int i)//回溯法计算
{
    int u;
    if (i == n) // 结束
    {
        cv = cv + w[x[n - 1]][1];
        if (cv <= v_best) // 小于最短路径
        {
            v_best = cv;// 更新最优解
        }
        for (int j = 0; j <= n - 1; j++)
        {
            x_best[j] = x[j];
            cout << x_best[j]<<' ';
        }
        cv = cv - w[x[n - 1]][1];//回溯（最大值回溯）
        return;
    }
    for (u = 2; u <= n; u++)
    {
        if (inX(u) == false && w[u][x[i - 1]] != -1)// 剩余可选城市
        {
            if (cv + w[x[i - 1]][u] <= v_best) // 加入后小于最短路径
            {
                x[i] = u; // 加入
                cv = cv + w[x[i - 1]][u]; // 更新当前解
                TSPrecursion(i + 1); // 搜索下一层
                x[i] = 0; // 回溯层数
                //因为需要回头来判断当前结点是否被访问过，所以需要回溯
                cv = cv - w[x[i - 1]][u];//回溯路径长度
            }
        }
    }
}

5.3 作业调度问题

• 题目描述：
  

注意1：排列树

这道题在复习的时候用代码调试一下

• 解空间树
  
• 遍历顺序
  123
  132 123
  213
  231 213 123
  321
  312 321

5.4 N皇后问题

注意1：排列树

• is_ok：判断当前位置是否可以放置
• queen：
  • 边界条件
  • 循环递归
• 时间复杂度：求排列问题。确认n个元素的满足某种性质的排列。其搜索树称为排列树，通常有n!个叶结点，因此遍历排列树需要时间为$O(n!)$

bool is_ok(int row)
{
    for (int j = 0; j != row; j++)
    {
        if (c[row] == c[j] || row - c[row] == j - c[j] || row + c[row] == j + c[j])//保证不在同一列&保证不在同一斜线
            return false;
    }
    return true;
}
void queen(int row){
    if (row == n)
    {
        total++;
        for (int j = 0; j < n; j++)
            cout << c[j] << ' ';
    }
    else
        for (int col = 0; col < n; col++)
        {
            c[row] = col;//row+1的递归过程已经保证不在同一排
            if (is_ok(row))
                queen(row + 1);
        }
}

到了这里，关于算法设计与分析 期末复习 北邮BUPT的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！