排序之堆排序-Toy模板网

这篇具有很好参考价值的文章主要介绍了排序之堆排序。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

在计算机科学中，排序是一种常见的操作。它的目标是将一组元素按照一定的顺序排列。不同的排序算法有不同的性能特性，选择哪种算法取决于具体的应用场景和需求。本文将介绍一种非常有效的排序算法——堆排序。

什么是堆排序？

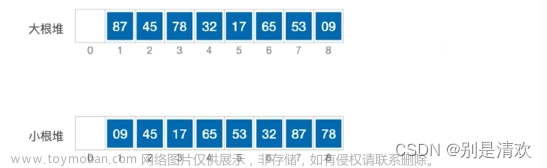
堆排序是一种基于二叉堆的比较排序算法。它的主要思想是将待排序的序列构造成一个大顶堆（或小顶堆），然后将堆顶的最大元素与末尾元素进行交换，再调整剩余元素为大顶堆，如此反复，直到整个序列有序。

堆排序的步骤

构建大顶堆：首先，我们需要将待排序的序列构造成一个大顶堆。这个过程可以通过从最后一个非叶子节点开始，依次向上调整每个节点来实现。
堆顶堆底进行交换：然后，我们将堆顶的元素（即当前最大的元素）与堆底的元素进行交换。这样，最大元素就位于了正确的位置。
调整剩余元素为大顶堆：最后，我们需要将剩余的元素重新调整为大顶堆。这个过程同样可以通过从最后一个非叶子节点开始，依次向上调整每个节点来实现。
重复以上步骤，直到整个序列有序：这就是堆排序的基本过程。

时间复杂度

时间复杂度：O(nlogn)

空间复杂度：O(1)。

代码实现

package sort;

import java.util.Arrays;
//堆排序
public class HeapSort {

	public static void main(String[] args) {
		int[] arr = {5,7,4,2,0,3,1,6};
		//构建大顶堆
		for(int i =arr.length;i>=0;i--) {
			adjust(arr, i, arr.length);
		}
		//堆顶堆底进行交换
		for(int j = arr.length-1;j>=0;j--) {
			int temp = arr[j];
			arr[j] =arr[0];
			arr[0] = temp;
			adjust(arr, 0, j);
		}
		System.out.println(Arrays.toString(arr));
	}
	/**
	 * 堆的维护
	 * @param arr
	 * @param parent
	 * @param length
	 */
	public static void adjust(int[] arr,int parent,int length) {
		int child = 2*parent+1;
		while(child<length) {
			//定义右孩子，找到左右孩子的最大值
			int rchild = child+1;
			if(rchild<length && arr[child]<arr[rchild]) {
				child++;
			}
			//父节点进行对比
			if(arr[parent]<arr[child]) {
				//父节点进行交换
				int temp = arr[parent];
				arr[parent] = arr[child];
				arr[child] = temp;
				parent = child;
				child = 2*child+1;
			}else {
				break;
			}
		}	
	}
}

总结

堆排序是一种非常高效的排序算法，其时间复杂度为O(nlogn)，空间复杂度为O(1)。虽然它的实现相对复杂一些，但是一旦理解了其基本思想，就可以很容易地掌握这种算法。希望这篇文章能帮助你更好地理解和应用堆排序。文章来源地址https://www.toymoban.com/news/detail-794948.html

到了这里，关于排序之堆排序的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！