Pybullet获取RGB图像和深度图像构建点云（Open3D）-Toy模板网

这篇具有很好参考价值的文章主要介绍了Pybullet获取RGB图像和深度图像构建点云（Open3D）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

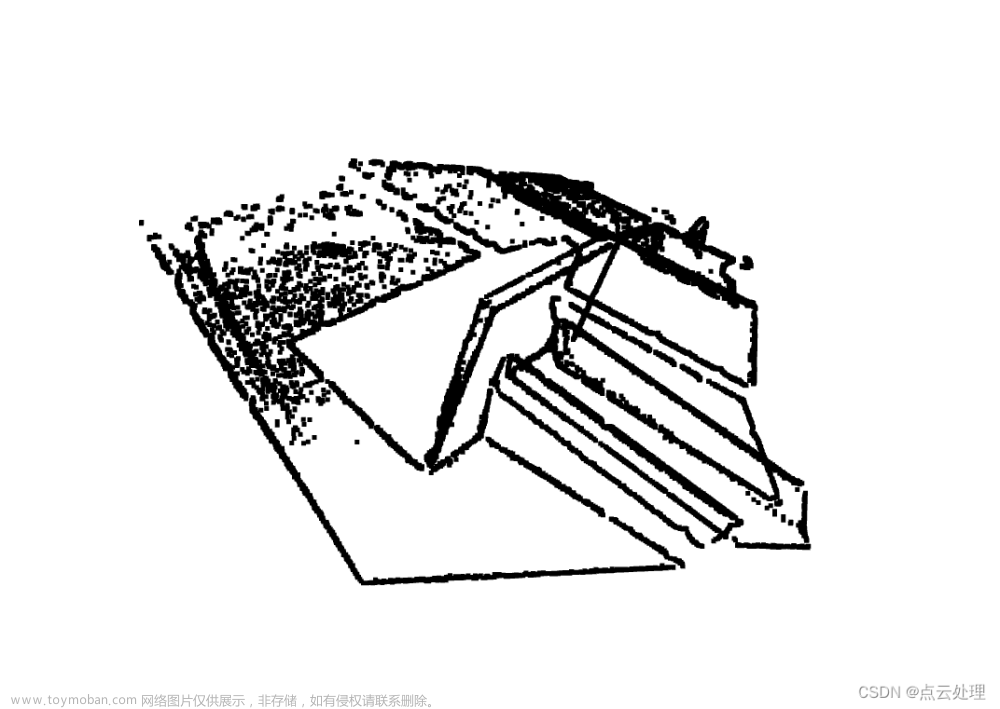
最近正在做点云分割相关的课题，数据集采集有点麻烦，想通过Pybullet先制作一批仿真合成数据集出来。虽然思路挺清晰，由RGB-D图像生成点云，但是中间有很多地方会卡住，所以写篇blog记录一下。

图像拍摄

图像的拍摄挺简单的，直接用Pybullet现成的函数就可以获取RGB图像和深度图像，就是先要对物体还有相机的位置朝向等做个设置。

import pybullet as p
import pybullet_data
import numpy as np
import cv2
import PIL.Image as Image
import open3d as o3d

# 连接引擎
_ = p.connect(p.GUI)
# 不展示GUI的套件
p.configureDebugVisualizer(p.COV_ENABLE_GUI, 1)
# 添加资源路径
p.setAdditionalSearchPath(pybullet_data.getDataPath())


planeUid = p.loadURDF("plane.urdf", useMaximalCoordinates=True)  # 加载一个地面
trayUid = p.loadURDF("tray/traybox.urdf", basePosition=[0, 0, 0])  # 加载一个箱子，设置初始位置为（0，0，0）
p.setGravity(0,0,-10)

width = 1080  # 图像宽度
height = 720   # 图像高度

fov = 50  # 相机视角
aspect = width / height  # 宽高比
near = 0.01  # 最近拍摄距离
far = 20  # 最远拍摄距离

cameraPos = [0,0,1]  # 相机位置
targetPos = [0,0,0]  # 目标位置，与相机位置之间的向量构成相机朝向
cameraupPos = [1,0,0]  # 相机顶端朝向

viewMatrix = p.computeViewMatrix(
    cameraEyePosition=cameraPos,
    cameraTargetPosition=targetPos,
    cameraUpVector=cameraupPos,
    physicsClientId=0
)  # 计算视角矩阵
projection_matrix = p.computeProjectionMatrixFOV(fov, aspect, near, far)  # 计算投影矩阵
w, h, rgb, depth, seg = p.getCameraImage(width, height, viewMatrix, projection_matrix, renderer=p.ER_BULLET_HARDWARE_OPENGL)
# 由此便可以得到RGB图像、深度图像、分割标签图像

图像存储

接下来就是将图像存储下来了，这里有挺多坑的。

彩色图像

彩色图像的存储还是比较简单的，我这里直接用OpenCV存，就是需要将RGB通道转换一下，OpenCV存储时的通道顺序有点不一样。

rgbImg = cv2.cvtColor(images[2], cv2.COLOR_BGR2RGB)
cv2.imwrite('image/rgb.jpg',rgbImg)

深度图像

坑1：深度图像一般的存储单位都是毫米，而Pybullet里的单位是米，所以需要做个换算。
坑2：需要对深度图像的深度值做一个透视变换，原理参考下文：《【3D数学】——透视变换与相机偏手性》，主要就是如下公式（符号意义看链接中的文章）： $m_3+\frac{m_4}{z}=z'\Rightarrow z= \frac{m_4}{z'-m_3}$
坑3：由于深度数值会超过255，因此深度图像需要存储成为int16格式，jpg文件只能存储int8的数据，因此需要存储成为png文件。
存储代码如下(做了个按键交互)：

i=1
# 开始渲染
while True:
    p.stepSimulation()
    images = p.getCameraImage(width, height, viewMatrix, projection_matrix, renderer=p.ER_BULLET_HARDWARE_OPENGL)
    
    keys = p.getKeyboardEvents()
    
    if ord("z") in keys and keys[ord("z")] & p.KEY_WAS_RELEASED:
        
        rgbImg = cv2.cvtColor(images[2], cv2.COLOR_BGR2RGB)      
        cv2.imwrite('image/rgb'+str(i)+'.jpg',rgbImg)

        depImg = far * near / (far - (far - near) * images[3])
        depImg = np.asanyarray(depImg).astype(np.float32) * 1000.  
        depImg = (depImg.astype(np.uint16))
        print(type(depImg[0,0]))
        depImg = Image.fromarray(depImg)
        depImg.save('image/depth'+str(i)+'.png')
        
        cv2.imwrite('image/seg'+str(i)+'.jpg',images[4])
        i=i+1

分割标签图像

这个图像的像素值就是0，1，…，代表每个物体的标签，重构点云暂时用不到。

内参计算

如果要通过RGB-D图像重建点云，那么必然需要相机的内参，但是Pybullet中的相机貌似只能计算得到投影矩阵，无法直接获取内参，那么就需要进行一定的计算获取内参参数。
这里还是先稍微介绍一下相关概念。

坐标系

pybullet相机,计算机视觉,opencv,python 图源：https://zhuanlan.zhihu.com/p/473172644
世界坐标系world：顾名思义。
相机坐标系camera：以相机的光心为原点，前为Z轴，右为X轴，下为Y轴。
图像坐标系xy：成像平面与光轴的交点为原点。真实情况下，图像平面是在光心Oc后面，所产生的图像是一个颠倒的画面。为了讨论方便，这里是将图像平面放到了Oc前面，因此此时图像平面的图像没有颠倒，而xy轴的方向与相机坐标系的方向相反，单位为mm。
像素坐标系：图像平面中图像左上角为原点，单位为pixel。
焦距：光心与成像平面之间的距离。

内外参

我们将世界到相机的变换称为相机的外参矩阵R，t。
我们将相机投影到图像的变换称为相机的内参矩阵K。
外参：将世界坐标系转换成相机坐标系。
内参：将相机坐标系转换成图像坐标系。
pybullet相机,计算机视觉,opencv,python 图源：https://zhuanlan.zhihu.com/p/473172644

fx = f / dx
fy = f / dy
f : 焦距长度，物理单位mm
dx、dy : x、y方向上一个像素分别代表多少mm
u0、v0 : 图像的中心像素坐标和图像原点像素坐标之间相差的横向和纵向像素数。理论值应该是图像宽度、高度的一半，但实际是有偏差的，一般摄像头越好越接近理论值。有些地方写作cx，cy。

大概算是介绍完了一些基础概念，然后开始从Pybullet中的投影矩阵得到内参。投影矩阵就是上文代码中的projection_matrix，输出为16个元素的行向量数组，需要提取一下变成4X4矩阵，Pybullet采用的是OpenGL中的投影矩阵，形式如下：

$\begin{bmatrix} \frac {2f_x} {r-l} & 0 & \frac {r+l} {r-l} & 0\\ 0 & \frac {2f_y} {t-b} & \frac {t+b} {t-b} &0 \\ 0 & 0 & \frac {-(f+n)} {f-n} & \frac {-2fn} {f-n} \\ 0 & 0 & -1 & 0 \end{bmatrix} \$
其中：
$\begin{cases} l=-c_x \\ r=W-c_x\\ b=-c_y \\ t=H-c_y \\ \end{cases}$
H、W分别为图像的高和宽，单位为pixel。
f为最远拍摄距离，n为最近拍摄距离。
那么投影矩阵又可以表示为
$\begin{bmatrix} \frac {2f_x} {W} & 0 & \frac {W-2c_x} {W} & 0\\ 0 & \frac {2f_y} {H} & \frac {H-2c_y} {H} &0 \\ 0 & 0 & \frac {-(f+n)} {f-n} & \frac {-2fn} {f-n} \\ 0 & 0 & -1 & 0 \end{bmatrix} \$
Pybullet得到的投影矩阵和上面的投影矩阵属于转置关系，其计算公式为：（pybullet已经帮你算好了）
pybullet相机,计算机视觉,opencv,python
因此做个一一对应就可以计算得到相机内参了，假设投影矩阵为P：
$\begin{cases} c_x=W/2 \\ c_y=H/2 \\ f_x = P[0,0]*W/2 \\ f_y = P[1,1]*H/2 \end{cases}$
OK，总算是把内参算好了，畸变这里就不考虑了。
接下来就简单了，Open3D读取然后重建一下就好了。

import open3d as o3d

color_image = o3d.io.read_image('image/rgb1.jpg')
depth_image = o3d.io.read_image('image/depth1.png')

rgbd_image = o3d.geometry.RGBDImage.create_from_color_and_depth(color_image, depth_image,convert_rgb_to_intensity=False)
intrinsic = o3d.camera.PinholeCameraIntrinsic(
    o3d.camera.PinholeCameraIntrinsicParameters.Kinect2DepthCameraDefault )
intrinsic.set_intrinsics(width=1080, height=720, fx=2.14450693*1080/2, fy=2.14450693*720/2, cx=1080/2, cy=720/2)

point_cloud = o3d.geometry.PointCloud.create_from_rgbd_image(rgbd_image, intrinsic)
o3d.visualization.draw_geometries([point_cloud])