排序算法-归并排序（含C语言代码示例）-Toy模板网

这篇具有很好参考价值的文章主要介绍了排序算法-归并排序（含C语言代码示例）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、算法介绍

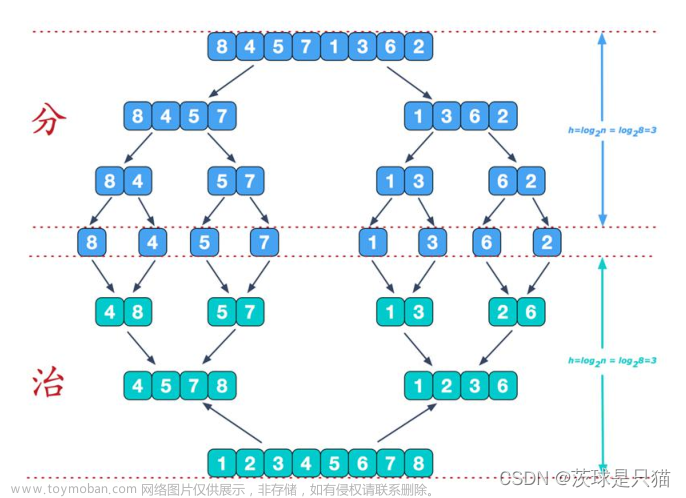
归并排序是一种基于分治思想的经典排序算法，其主要思想是将待排序的数组分割成两个子数组，分别对这两个子数组进行递归排序，然后将排好序的子数组合并起来得到最终有序数组。整个归并排序的过程可以分为三个步骤：分割、排序和合并。

首先，在分割步骤中，算法将待排序数组递归地分成两半，直到每个子数组的长度为1或0。这一步骤确保了每个子数组都是有序的。

其次，在排序步骤中，对每一对有序的子数组进行合并排序。这里使用了一个辅助数组来存储排序后的元素，然后将结果复制回原始数组。

最后，在合并步骤中，将排好序的两个子数组合并成一个有序数组。这一步骤是整个归并排序的关键，通过比较两个子数组的元素大小，并依次合并到辅助数组中，最终得到完全有序的数组。

归并排序的时间复杂度为O(n log n)，其中n是待排序数组的长度。虽然它在时间复杂度上不如快速排序那么优越，但归并排序具有稳定性，且对于链表等非连续存储结构也适用，因此在实际应用中具有一定的优势。文章来源地址https://www.toymoban.com/news/detail-795524.html

二、代码示例

int min(int a, int b) {
    return a < b ? a : b;
}
void merge_sort(int index[], int len) {
    int *a = index;
    int *b = (int *) malloc(len * sizeof(int));
    int seg, start;
    for (seg = 1; seg < len; seg += seg) {
        for (start = 0; start < len; start += seg * 2) {
            int low = start, mid = min(start + seg, len), high = min(start + seg * 2, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        int *temp = a;
        a = b;
        b = temp;
    }
    if (a != index) {
        int i;
        for (i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    free(b);
}

到了这里，关于排序算法-归并排序（含C语言代码示例）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！