目录
1 问题:如果要考察的概率模型(抽奖)里,基础中奖概率一直在变化怎么办?
1.1 基础问题,抽奖抽中的概率会变化
1.2 概率稳定的老模型,有什么问题?
1.3 比如:构建这样的一个新模型
2 用excel 计算这些概率
2.1 不用几何分布,但是照样可以求第n次是第一次成功的概率
2.1.1 计算过程
2.1.2 结论1
3 对比 概率变化的抽奖的好处
3.1 和几何分布的对比
3.1.1 最显著的是方差也变得集中
3.2 改变原始概率和增加的概率变化很多
3.2.1 变化模式,基础成功=10%,每次增加1%,几何分布保持概率10%
3.2.2 变化模式,基础成功=10%,每次增加5%,几何分布保持概率10%
3.2.3 变化模式,基础成功=30%,每次增加1%,几何分布保持概率30%
3.2.4 变化模式,基础成功=30%,每次增加5%,几何分布保持概率30%
3.3 其实,概率变化的函数还可以各种改进设计等
4 n次不全失败的概率=n次中至少成功1次的概率 = Σ 第n次成功(前面都失败)概率
5 如果在这个基础上,需要求条件概率呢?
6 这个概率不断增加的模型,pdf的函数图形和具体数值关系很大
7 EXCEL if函数 判断来模拟? 可以试试
8 如果用VBA模拟,修改下代码
9 这个和那几种 zhuanpan 的概率模型
1 问题:如果要考察的概率模型(抽奖)里,基础中奖概率一直在变化怎么办?
1.1 基础问题,抽奖抽中的概率会变化
- 有时候概率并不是固定的,而是会发生变化的
- 如果概率发生变化了,就不能套用一般的概率模型了
- 需要用一些其他办法计算了
- 复杂的高等数学手段?
- 写代码硬模拟? 模特卡洛模拟?
- EXCEL也可以解决部分这种问题
下面尝试用EXCEL 和 VBA解决一些这种问题
1.2 概率稳定的老模型,有什么问题?
- 概率稳定的抽奖模型,一般可以用 几何分布来看
- 如果概率够高,那么中奖的期望次数很小,狠容易达到
- 可以参考我之前的 几何分布的内容
概率论的学习和整理8: 几何分布_奔跑的犀牛先生的博客-CSDN博客几何分布_几何分布https://blog.csdn.net/xuemanqianshan/article/details/126149038?spm=1001.2014.3001.5502
- 如果概率比较低,比如10%这种,看着还不算很低,虽然期望次数为10
- 但是方差比较大,很多运气不好人可能20次,30次才能抽到,有的期望次数甚至到了100多次,虽然那种情况的概率也很低
- 但是这样不同人的抽奖感受就差别很大,这个就是问题所在了。
- 也就是很多游戏的抽奖,为什么都要加保底次数等设计了!

1.3 比如:构建这样的一个新模型
- 成功概率初始为 0.1
- 如果不成功每次加0.01,直到成功为止
- 任意一次成功后,下次成功概率重新回到0.1
- (其实可以有关于失败次数N 更复杂的概率公式,先构建一个这样的)
2 用excel 计算这些概率
2.1 不用几何分布,但是照样可以求第n次是第一次成功的概率
- 第n次才成功的概率 = 前面n-1 都失败,第n次成功的概率
2.1.1 计算过程
- 几何分布,p(x=n) =(1-p)^(1-n)*p
- 因为几何分布的概率是稳定不变的,成功一直=p,失败概率=1-p,所以n-1次失败可以简化为(1-p)^(n-1)
- 现在概率变化就写成(大写只是为了好看)
- p(x=n) =(1-P1)(1-P2)*....*(1-P(n-1))*Pn
- 只要注意,每次的Pi 或者(1-Pi)都是变化不同的,这个虽然手算很麻烦,但是EXCEL算起来很简单。

- 第1列,次数n
- 第2列,第n次,单次试验失败概率
- 第3列,第n次,单次试验成功概率
- 第4列,n次连续都失败概率,
- 第5列,n次中至少有1次成功的概率
- 第6列,前面n-1次都失败+第n次成功的这个事件的概率 (多个n的事件对应的就是随机变量)
- 后面就是求 Σpdf, 期望等!
2.1.2 结论1
- 用EXCEL拉表很方便结算,有限次数,次数不多的这个公式
- p(x=n) =失败n-1的累计概率*最后一次成功的概率
- p(x=n) =(1-P1)(1-P2)*....*(1-P(n-1))*Pn
- 即使不用几何分布也可以用相同的思想求 最后一次才成功的概率!
- 表上,第n成功(前面都失败)概率 这一列就是 类似 几何概率的 第n次才成功的概率
- 表上,n次中至少成功1次的概率 这一列就是 非全失败的概率
3 对比 概率变化的抽奖的好处
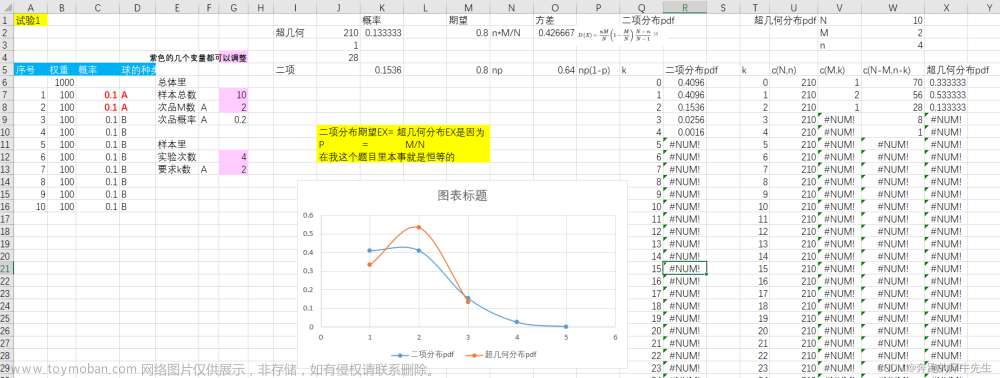
3.1 和几何分布的对比
- 左边,是每次试验,成功和失败概率都在变化的模型 (实验组)
- 右边,是每次试验概率不变的,几何分布,用于对比(对照组)

差异总结
提高概率的模式成为A模式,几何分布称为B模式
1 很明显,A模式因为成功概率逐渐增加,第一次成功的期望次数肯定会变小,也即变容易了,这个是6.8次,而几何分布是10次,这个是显然的
2 A模式的期望次数更小
3 A模式的方差大幅度降低,比几何分布好很多,这个应该是最优秀的地方
这里可能被数据影响的假象
- 因为我用的A模式,基础成功概率10%,而每次只增加1%,所以概率变化并不明显,
- 但是即使这样的情况,方差的缩小很明显!很优秀
3.1.1 最显著的是方差也变得集中
- 方差被拍扁了
- 就是方差变得更集中了,这个是很明显的
- 也就是,提高了一些概率,抽奖获得均值会变快,但是最明显的就是玩家抽奖的方差变小
- 因为方差得这个被压扁得特点,也就是能保证,绝大多数人的体验变得更好。!

3.2 改变原始概率和增加的概率变化很多
这里可能被数据影响的假象
- 多种情况下,增加概率的模式下,对比 相同基础成功概率的几何分布
- 即使每次增加概率很小,方差都能显著的缩小
- 虽然概率也一定会增加,但可能增加得不够显著(取决于增加的概率/基础成功概率 比例)
- 虽然期望也一定会变小,但变小幅度不如方差明显,不算很显著
3.2.1 变化模式,基础成功=10%,每次增加1%,几何分布保持概率10%
下面这个同上图

3.2.2 变化模式,基础成功=10%,每次增加5%,几何分布保持概率10%

3.2.3 变化模式,基础成功=30%,每次增加1%,几何分布保持概率30%

3.2.4 变化模式,基础成功=30%,每次增加5%,几何分布保持概率30%

- 这里现实的 Σpdf 和 期望数字出问题,是因为
- 初始概率足够高,一定次数下就必成了。

3.3 其实,概率变化的函数还可以各种改进设计等
- 比如固定某些次必须中奖
- 读之前的失败次数k 作为增加概率的系数的,而不是每次固定增加0.01,比如是0.01*K^2
- 甚至可以搞分段函数
- 还有些搞一些幸运值,其实 “幸运值--增加概率” 之间,比然是有个对应函数关系得,这个函数关系式可以简单,可以复杂,可以搞成各种各样得曲线形状


4 n次不全失败的概率=n次中至少成功1次的概率 = Σ 第n次成功(前面都失败)概率
- 可以看到
- n次不全失败的概率=n次中至少成功1次的概率 = Σ第n次成功(前面都失败)概率
- n次至少成功1次的概率: n次中只要成功次数>=1次就算,包括成功1次,成功2次,,,,等等,也不在乎是第几次成功
- 第n次成功(前面都失败)概率: 必须是前面n-1都失败,刚好第n 次成功

5 如果在这个基础上,需要求条件概率呢?
比如如下问题
前面假设相同
现在要求,前面9次都失败时,后面继续抽,成功抽中1次奖励就停止的概率
也就是想知道,如果已知前面9次都失败,后面继续抽还要多少次能抽中奖励?
其实是个条件概率
而条件概率的公式
- P(A|B) =P(AB) / P(B)
- P(最后1次成功|前9次都失败) =P(前9次都失败 & 最后一次成功) / P(前9次都失败的概率)
- 从条件概率的定义看
- P(前9次都失败 & 最后一次成功) = P(最后1次成功概率) 去掉前9次成功的那些变量和那些那些变量对应的概率即可!!!
- P(前9次都失败的概率)= 很简单得前9次失败概率*连乘
- P(最后1次成功|前9次都失败)= P(最后1次成功概率) /P(前9次都失败的概率)
- 而且 Σpdf=1


6 这个概率不断增加的模型,pdf的函数图形和具体数值关系很大
概率函数pdf的变化也和初始概率,增加概率等关系很大
- 我写的那篇几何分布里有详细考虑这个,
- 这里也一样
- 如果原始概率高,增加少,则是 刚开始就是最高点
- 增加概率/初始成功概率,这个比例也很重要



7 EXCEL if函数 判断来模拟? 可以试试
8 如果用VBA模拟,修改下代码
可以写个程序模拟下
蒙特卡洛模拟
平均概率random
还可以考虑其他分布的概率分布、
比如不平均概率的
改进的蒙特卡洛模拟
还有算了一个超几何分布’
但是不是等概率模型,如何处理的一个例子
这些特殊例子
是否可以变成公式??
9 这个和那几种 zhuanpan 的概率模型
是不是都有关系??文章来源:https://www.toymoban.com/news/detail-795781.html
原理和公式改写?文章来源地址https://www.toymoban.com/news/detail-795781.html
到了这里,关于概率论的学习和整理14: 概率发生变化的抽奖,如何计算概率?( 缺 VBA模拟部分)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!