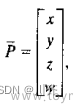[足式机器人]Part3 机构运动学与动力学分析与建模 Ch00-3(1) 刚体的位形 Configuration of Rigid Body-Toy模板网

这篇具有很好参考价值的文章主要介绍了[足式机器人]Part3 机构运动学与动力学分析与建模 Ch00-3(1) 刚体的位形 Configuration of Rigid Body。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

本文仅供学习使用，总结很多本现有讲述运动学或动力学书籍后的总结，从矢量的角度进行分析，方法比较传统，但更易理解，并且现有的看似抽象方法，两者本质上并无不同。

2024年底本人学位论文发表后方可摘抄
若有帮助请引用
本文参考：
.

食用方法
如何表达刚体在空间中的位置与姿态
姿态参数如何表达？不同表达方式直接的转换关系？
旋转矩阵？转换矩阵？有什么意义和性质？转置代表什么？
如何表示连续变换？——与RPY有关
齐次坐标的意义——简化公式？
务必自己推导全部公式，并理解每个符号的含义

刚体的位形可以用六个独立（坐标）参数完全描述：三个位置参数用于描述运动刚体上运动坐标系 $\left\{ M \right\}$ 原点 $M$ 在固定坐标系 $\left\{ F \right\}$ 的投影参数，三个转动参数用于描述运动坐标系 $\left\{ M \right\}$ 的基矢量相对于固定坐标系 $\left\{ F \right\}$ 的基矢量的姿态，而描述这种姿态的变换，则是需要确定矩阵 $\left[ Q_{\mathrm{M}}^{F} \right]$ 。

因此为描述空间坐标系中任意一刚体的运动状态，首先需要描述刚体的位置矢量 $\vec{R}_{\mathrm{M}}^{F}$ 与姿态矩阵 $\left[ Q_{\mathrm{F}}^{M} \right]$ （表述为：坐标系 $\left\{ M \right\}$ 的基矢量在坐标系 $\left\{ F \right\}$ 下的线性表达，描述了 $\left\{ M \right\}$ 的姿态，同时也可理解为将坐标系 $\left\{ F \right\}$ 通过姿态矩阵进行旋转变换，得到新的坐标系 $\left\{ M \right\}$ ）

广义参考系坐标 Reference Coordinates：为方便后续动力学方程的建立与推导，常用广义坐标矢量参数 $\vec{q}_{\mathrm{M}}^{F}$ 来描述运动刚体的形位，其中：
$\vec{q}_{\mathrm{M}}^{F}=\left[ \vec{R}_{\mathrm{M}}^{F},\vec{\theta}_{\mathrm{M}}^{F} \right]$

$\vec{\theta}_{\mathrm{M}}^{F}$ 可以用多种方法来描述（通常包含3或4个角度参数），这些角度参数用于描述姿态矩阵（旋转矩阵） $\left[ Q_{\mathrm{F}}^{M} \right]$

对于刚体的运动状态而言，其运动坐标系的原点 $M$ 的位置矢量 $\vec{R}_{\mathrm{M}}^{F}$ 表示与点的运动状态表示相同，因此需要探究如何用角度参数来描述转换矩阵。

3. 转换矩阵与旋转矩阵——刚体的位置与姿态描述

转换矩阵用于表述两个坐标系 $\left\{ A:\left( \vec{i}^A,\vec{j}^A,\vec{k}^A \right) \right\}$ 与 $\left\{ B:\left( \vec{i}^B,\vec{j}^B,\vec{k}^B \right) \right\}$ 的基矢量之间的转换关系：
$\left[ \begin{array}{c} \vec{i}^B\\ \vec{j}^B\\ \vec{k}^B\\ \end{array} \right] =\left[ Q_{\mathrm{B}}^{A} \right] ^{\mathrm{T}}\left[ \begin{array}{c} \vec{i}^A\\ \vec{j}^A\\ \vec{k}^A\\ \end{array} \right]$

其中，转换矩阵 $\left[ Q_{\mathrm{B}}^{A} \right] ^{\mathrm{T}}$ 表示坐标系 $\left\{ B \right\}$ 的基矢量在坐标系 $\left\{ A \right\}$ 中的表达，可将向量在不同的基矢量坐标系下进行表示。特殊的：若将基矢量替换成对应基矢量的向量投影，则可以表示为：两个原点重合的坐标系中，对同一向量的不同表达的转换关系；

上式也可以理解为：对坐标系 $\left\{ A:\left( \vec{i}^A,\vec{j}^A,\vec{k}^A \right) \right\}$ 进行了 $\left[ Q_{\mathrm{A}}^{B} \right]$ 的旋转(从坐标系 $\left\{ A \right\}$ 旋转为坐标系 $\left\{ B \right\}$ 的姿态) ，此时将转换矩阵与向量的运算理解为张量与向量的运算，即得到了旋转后的向量在坐标系 $\left\{ A \right\}$ 中的表达，此时实际上，对原始坐标系 $\left\{ A \right\}$ 的基矢量同样进行了旋转，形成了新坐标系 $\left\{ B \right\}$ 的基矢量，其仍在坐标系 $\left\{ A \right\}$ 下表达。

$\left[ \begin{array}{c} {r^{\prime}}_{1}^{A}\\ {r^{\prime}}_{2}^{A}\\ {r^{\prime}}_{3}^{A}\\ \end{array} \right] =\left[ Q \right] \left[ \begin{array}{c} r_{1}^{A}\\ r_{2}^{A}\\ r_{3}^{A}\\ \end{array} \right]$

目前，人们采用不同的角度参数 $\vec{\theta}$ 来对旋转矩阵进行描述

Representing an orientation —— from definition
将原矢量进行旋转变换，得到该坐标系下新矢量的坐标投影参数：
$\vec{R}_{\mathrm{p}^{\prime}}^{F}=\left[ Q\right] \vec{R}_{\mathrm{p}}^{F}$

Changing the reference frame
对坐标系进行转换，基于坐标系 $\left\{ A \right\}$ 中的该矢量的坐标投影参数 $\vec{R}_{\mathrm{p}}^{A}$ ，得到该矢量在坐标系 $\left\{ B \right\}$ 中的坐标投影参数 $\left( \vec{R}_{\mathrm{p}}^{A} \right) ^B$ ：
$\left( \vec{R}_{\mathrm{p}}^{A} \right) ^B=\left[ Q_{\mathrm{A}}^{B} \right] \vec{R}_{\mathrm{p}}^{A}$

3.1 轴角变换

[足式机器人]Part3 机构运动学与动力学分析与建模 Ch00-3(1) 刚体的位形 Configuration of Rigid Body,运动学与动力学,足式机器人,机器人
假设两个坐标系 $\left\{ A \right\}$ 与 $\left\{ B \right\}$ 的原点重合，其中坐标系 $\left\{ B \right\}$ 为坐标系 $\left\{ A \right\}$ 绕轴 $\vec{v}^F$ （单位向量）旋转 $\theta$ 所得到的。因此对于坐标系 $\left\{ A \right\}$ 中的点 $P$ ，经过转换后，得到点 $P^{\prime}$ ，此时点 $P^{\prime}$ 在坐标系 $\left\{ B \right\}$ 中的矢量投影与点 $P$ 在坐标系 $\left\{ A \right\}$ 中的投影分量相同。而在转换过程中，点 $P^{\prime}$ 在坐标系 $\left\{ A \right\}$ 中的表达发生变化，即有： $\left[ {P^{\prime}}_{1}^{\mathrm{B}},{P^{\prime}}_{2}^{\mathrm{B}},{P^{\prime}}_{2}^{\mathrm{B}} \right] =\left[ P_{1}^{A},P_{2}^{A},P_{2}^{A} \right]$ ，因此对式 $\left[ \begin{array}{c} \vec{i}^B\\ \vec{j}^B\\ \vec{k}^B\\ \end{array} \right] =\left[ Q_{\mathrm{B}}^{A} \right] ^{\mathrm{T}}\left[ \begin{array}{c} \vec{i}^A\\ \vec{j}^A\\ \vec{k}^A\\ \end{array} \right]$ 有：
$\begin{split} &\left[ \begin{array}{c} \vec{i}^B\\ \vec{j}^B\\ \vec{k}^B\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} P_{1}^{\mathrm{B}}\\ P_{2}^{\mathrm{B}}\\ P_{3}^{\mathrm{B}}\\ \end{array} \right] =\left[ \begin{array}{c} \vec{i}^A\\ \vec{j}^A\\ \vec{k}^A\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} P_{1}^{A}\\ P_{2}^{A}\\ P_{3}^{A}\\ \end{array} \right] \\ &\Rightarrow \left( \left[ Q_{\mathrm{B}}^{A} \right] ^{\mathrm{T}}\left[ \begin{array}{c} \vec{i}^A\\ \vec{j}^A\\ \vec{k}^A\\ \end{array} \right] \right) ^{\mathrm{T}}\left[ \begin{array}{c} P_{1}^{\mathrm{B}}\\ P_{2}^{\mathrm{B}}\\ P_{3}^{\mathrm{B}}\\ \end{array} \right] =\left[ \begin{array}{c} \vec{i}^A\\ \vec{j}^A\\ \vec{k}^A\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} P_{1}^{A}\\ P_{2}^{A}\\ P_{3}^{A}\\ \end{array} \right] \\ &\Rightarrow \left[ \begin{array}{c} \vec{i}^A\\ \vec{j}^A\\ \vec{k}^A\\ \end{array} \right] ^{\mathrm{T}}\left[ Q_{\mathrm{B}}^{A} \right] \left[ \begin{array}{c} P_{1}^{\mathrm{B}}\\ P_{2}^{\mathrm{B}}\\ P_{3}^{\mathrm{B}}\\ \end{array} \right] =\left[ \begin{array}{c} \vec{i}^A\\ \vec{j}^A\\ \vec{k}^A\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} P_{1}^{A}\\ P_{2}^{A}\\ P_{3}^{A}\\ \end{array} \right] \\ &\Rightarrow \left[ Q_{\mathrm{B}}^{A} \right] \left[ \begin{array}{c} P_{1}^{\mathrm{B}}\\ P_{2}^{\mathrm{B}}\\ P_{3}^{\mathrm{B}}\\ \end{array} \right] =\left[ \begin{array}{c} P_{1}^{A}\\ P_{2}^{A}\\ P_{3}^{A}\\ \end{array} \right] =\left[ \begin{array}{c} {P^{\prime}}_{1}^{\mathrm{B}}\\ {P^{\prime}}_{2}^{\mathrm{B}}\\ {P^{\prime}}_{3}^{\mathrm{B}}\\ \end{array} \right] \end{split}$ 文章来源地址https://www.toymoban.com/news/detail-795847.html