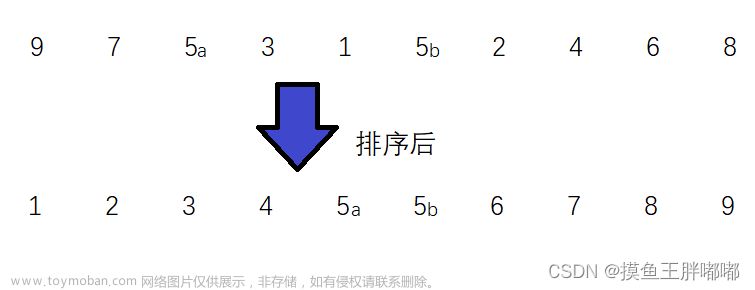
一.归并是什么?
相信朋友们应该做过一类题,合并两个有序数组,在链表里也有合并两个单链表的oj题,那我们稍微回顾一下
题目一:合并有序数组
普通思路:
1.定义一个第三方数组,用来临时归并排序
2.分别比较两个数组,小者先放进临时数组中
3.补充未排完的数组
4.将临时数组的值拷贝进返回数组nums1
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
int sum[m+n];
int i=0,j=0,count=0;
//比较取小尾插
while(i<m&&j<n)
{
if(nums1[i]<=nums2[j])
{
sum[count++]=nums1[i++];
}
else
{
sum[count++]=nums2[j++];
}
}
//补充
while(i<m)
{
sum[count++]=nums1[i++];
}
while(j<n)
{
sum[count++]=nums2[j++];
}
memcpy(nums1,sum,sizeof(int)*(m+n));
}
题目二:合并有序链表
普通思路:
1.定义并维护指针head tail
2.判断两种特殊情况
3.循环比较尾插
4.若有未链接的连结则直接尾插
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
struct ListNode *head=NULL, *tail=NULL;
//两种特殊情况
if (list1 == NULL)
return list2;
if (list2 == NULL)
return list1;
while (list1 && list2) {
if (list1->val <= list2->val) {
//初始状态判定
if (tail == NULL)
head = tail = list1;
else {
tail->next = list1;
tail = list1;
}
if (list1)
list1 = list1->next;
} else {
//初始状态判定
if (tail == NULL)
head = tail = list2;
else {
tail->next = list2;
tail = list2;
}
if (list2)
list2 = list2->next;
}
}
//补充
if(list1) tail->next=list1;
else tail->next=list2;
return head;
}
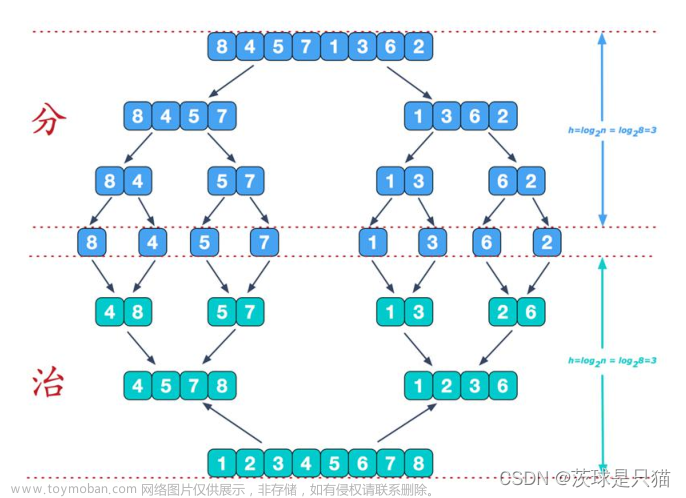
二.归并排序
字面意思,归并排序是通过将数据分别归并比较最终成为有序
建立一个临时数组,然后将数据两两归并放入临时数组,最终将有序数组拷贝回目标数组中
1.递归式归并
- 首先动态开辟一个临时数组tmp
void Mergesort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
}
_Mergesort(a, 0, n - 1, tmp);
free(tmp);
}
- 然后编写子程序_Mergesort
void _Mergesort(int* a, int begin, int end, int* tmp)
四个参数,目标无序数组,目标起始下标,目标结束下标,已开辟的数组
- 确定递归结束条件,归并的区间<=1时则可视为有序
if (begin >= end)
return;
- 分离出归并区间,取中间下标,递归式分离
//分离[begin1,end1][begin2,end2]
int mid = (begin + end) / 2;
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
_Mergesort(a, begin1, end1, tmp);
_Mergesort(a, begin2, end2, tmp);
- 开始归并,这里的小细节是递归一次拷贝一组,边排边拷贝,不然可能导致数据丢失
//归并
int i = begin;
while (begin1<=end1&&begin2<=end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a+begin, tmp+begin, sizeof(int) * (end - begin + 1));
程序编写完成,测试一下
void test()
{
int a[11] = { 9,6,7,3,1,5,7,10,0,0,1 };
Mergesort(a, 11);
for (size_t i = 0; i < 11; i++)
{
printf("%d ", a[i]);
}
}

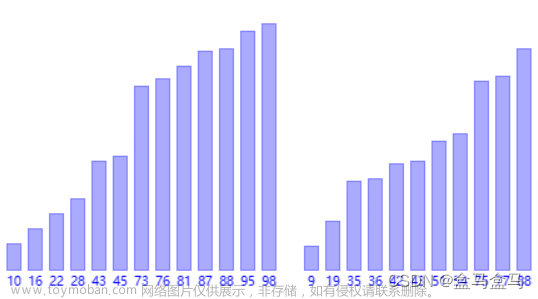
2.非递归式的归并排序
非递归思路是由分散的每个数据两两归并,然后成倍增加归并个体的数量,如下图 文章来源:https://www.toymoban.com/news/detail-796359.html
文章来源:https://www.toymoban.com/news/detail-796359.html
- 先将组内数量设置为gap=1
int gap = 1;
while (gap < n)
{
//...
gap *= 2;
}
- 分理待归并数组
for (size_t i = 0; i < n ;i+=2*gap)
{
//分出两组区域
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//...
}
- 如果是单纯end1或begin2越界出错则直接跳出,如果end2出错那就直接将end2的边界处理为n-1
// 边界的处理
if (end1 >= n || begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
- 然后开始基本环节归并并拷贝回目标数组
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));
- 最后释放临时数组
free(tmp);
测试一下:
void test()
{
int a[11] = { 9,6,7,3,1,5,7,10,0,0,1 };
MergeNRsort(a, 11);
for (size_t i = 0; i < 11; i++)
{
printf("%d ", a[i]);
}
}

两个完整代码已上传码云:递归和非递归归并排序
感谢大佬评论和建议文章来源地址https://www.toymoban.com/news/detail-796359.html
到了这里,关于排序嘉年华———归并排序的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!






![[数据结构 -- 手撕排序算法第七篇] 递归实现归并排序](https://imgs.yssmx.com/Uploads/2024/02/573259-1.png)