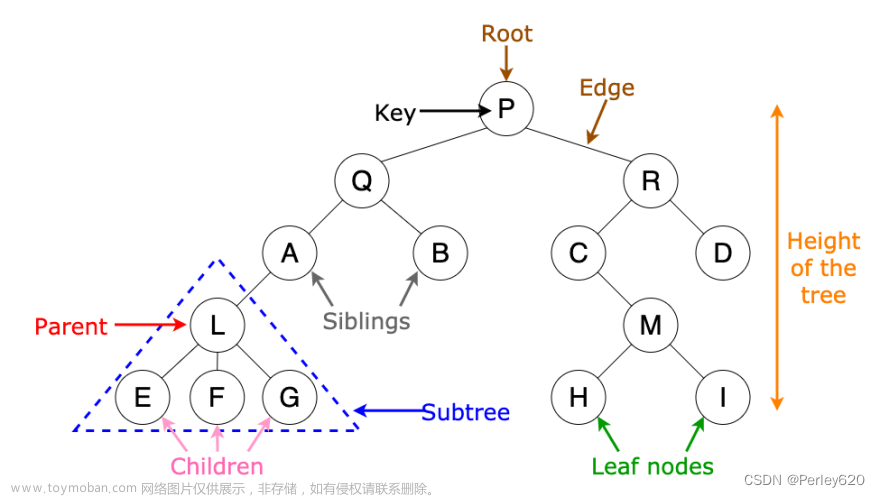
头文件(结构体定义与函数声明):
#ifndef BTREE_H_INCLUDED
#define BTREE_H_INCLUDED
#include<stdbool.h>
#include<stdlib.h>//NULL的头文件
#define m 3//BTree的阶每个节点至多有m棵子树且非终端节点至少有[m/2]棵子树
#define KeyType int
#define Record int
typedef enum{OK,ERROR}Status;
typedef struct BTNode
{
int keynum;//节点中关键字的个数
struct BTNode *parent;
KeyType Key[m+1];//关键字向量0号单元未用
struct BTNode* ptr[m+1];//子树指针向量
Record* recptr[m+1];//记录指针向量0号单元未用
}BTNode,*BTree;//均多留出一个单元分裂时使用
typedef struct
{
BTNode *pt;//指向找到的节点
int i;//在节点中的关键字序号1到m
int tag;//1查找成功0查找失败
}Result;//B树的查找结果类型
int Search(BTree p,KeyType K);
Result SearchBTree(BTree T,KeyType K);
void Insert(BTree q,int i,KeyType x,BTree ap);
void split(BTree q,int s,BTree ap);
void NewRoot(BTree *T,BTree p,KeyType x,BTree ap);
Status InsertBTree(BTree *T,KeyType K,BTree q,int i);
void Merge(BTree v);
void Delete(BTree v,int i);
Status DeleteBTree(BTree T,KeyType K);
#endif // BTREE_H_INCLUDED
函数实现
(需要在源文件即后缀为.c的文件中实现,否则编译器会报错,重复定义函数):
#include "BTree.h"
#include<math.h>
int s=ceil((double)m/2);
int Search(BTree p,KeyType K)
{
int i;
for(i=1;i<=p->keynum&&p->Key[i]<K;i++);
if(p->Key[i]!=K)i--;
return i;
}
Result SearchBTree(BTree T,KeyType K)
{
BTree p=T;
BTree q=NULL;
bool found=false;int i=0;
while(p&&!found)
{
i=Search(p,K);//在p->Key中查找使得p->Key[i]<=K<p->Key[i+1]
if(i>0&&p->Key[i]==K)found=true;
else
{
q=p;p=p->ptr[i];
}
}
if(found)return (Result){p,i,1};
else return (Result){q,i,0};
}
void Insert(BTree q,int i,KeyType x,BTree ap)
{
int j;
for(j=q->keynum;j>i;j--)
{
q->Key[j+1]=q->Key[j];
q->ptr[j+1]=q->ptr[j];
q->recptr[j+1]=q->recptr[j];
}
q->Key[i+1]=x;
q->ptr[i+1]=ap;
q->recptr[i+1]=NULL;
if(ap!=NULL)
{
ap->parent=q;
}
q->keynum++;
return;
}
void split(BTree q,int s,BTree ap)
{//ap将成为q的右兄弟
ap=(BTree)malloc(sizeof(BTNode));
ap->keynum=m-s;
ap->parent=q->parent;
for(int j=s+1;j<=m;j++)
{
ap->Key[j-s]=q->Key[j];
ap->ptr[j-s]=q->ptr[j];
ap->recptr[j-s]=q->recptr[j];
if(q->ptr[j]!=NULL)
{
q->ptr[j]->parent=ap;
}
}
q->keynum=s;
if(q->parent!=NULL)
{
Insert(q->parent,Search(q->parent,q->Key[s]),q->Key[s],ap);
}
return;
}
void NewRoot(BTree *T,BTree p,KeyType x,BTree ap)
{
BTree root=(BTree)malloc(sizeof(BTNode));
root->parent=NULL;
root->keynum=1;
root->Key[1]=x;
root->ptr[0]=p;
root->ptr[1]=ap;
root->recptr[0]=NULL;
root->recptr[1]=NULL;
p->parent=root;
ap->parent=root;
*T=root;
return;
}
Status InsertBTree(BTree *T,KeyType K,BTree q,int i)
{
KeyType x=K;bool finished=false;
BTree ap=NULL;
while(q&&!finished)
{
Insert(q,i,x,ap);//将x和ap分别插入q->Key[i+1]和q->ptr[i+1]
if(q->keynum<m)finished=true;
else//分裂节点
{//s=m/2向上取整
split(q,s,ap);
x=q->Key[s];//将q->Key[s+1,m],q->ptr[s,m]和q->recptr[s+1,m]移入新节点*ap
q=q->parent;
if(q)i=Search(q,x);
}
}
if(!finished)//T是空树或根节点已经分裂为节点关*q和*ap
NewRoot(T,q,x,ap);//生成含信息(T,x,ap)的新的根节点关*T,原T和ap为子树指针
return OK;
}
void Merge(BTree v)
{
if(v->keynum>=s-1)return;
BTree pt=v->parent;
if(pt==NULL)return;
int j;
for(j=0;j<=pt->keynum;j++)if(pt->ptr[j]==v)break;
BTree r=NULL,l=NULL;
if(j<pt->keynum)r=pt->ptr[j+1];
if(j>0)l=pt->ptr[j-1];
if(r)
{
int k=v->keynum;
v->ptr[++k]=r->ptr[0];
v->recptr[k]=pt->recptr[j+1];
v->Key[k]=pt->Key[j+1];
for(int i=1;i<=r->keynum;i++)
{//合并时不一定是终端节点所以需要考虑子树的改变
v->Key[++k]=r->Key[i];
v->ptr[k]=r->ptr[i];
v->recptr[k]=r->recptr[i];
}
v->keynum=k;
for(k=j+1;k<pt->keynum;k++)
{
pt->Key[k]=pt->Key[k+1];
pt->ptr[k]=pt->ptr[k+1];
pt->recptr[k]=pt->recptr[k+1];
}
pt->keynum--;
Merge(pt);
}
else
{
int k=++l->keynum;
l->ptr[k]=v->ptr[0];
l->recptr[k]=pt->recptr[j];
l->Key[k]=pt->Key[j];
for(int i=1;i<=v->keynum;i++)
{
l->Key[++k]=v->Key[i];
l->ptr[k]=v->ptr[i];
l->recptr[k]=v->recptr[i];
}
l->keynum=k;
for(int i=j;i<pt->keynum;i++)
{
pt->Key[i]=pt->Key[i+1];
pt->recptr[i]=pt->recptr[i+1];
pt->ptr[i]=pt->ptr[i+1];
}
pt->keynum--;
Merge(pt);
}
return;
}
void Delete(BTree v,int i)
{
BTree pt=v->parent;
if(v->keynum>=s||pt==NULL)
{//该节点的关键字数目不小于s
for(int j=i;j<v->keynum;j++)
{
v->Key[j]=v->Key[j+1];
v->recptr[j]=v->recptr[j+1];
}
v->keynum--;
}
else if(v->keynum==s-1)
{
int j;
for(j=0;j<=pt->keynum;j++)
{
if(pt->ptr[j]==v)break;
}
BTree r=NULL,l=NULL;
if(j<pt->keynum)r=pt->ptr[j+1];
if(j>0)l=pt->ptr[j-1];
if(r&&r->keynum>s-1)
{
int k;
for(k=i;k<v->keynum;k++)
{//此时v一定是终端节点所以不用考虑子树
v->Key[k]=v->Key[k+1];
v->recptr[k]=v->recptr[k+1];
}
v->Key[k]=pt->Key[j+1];
pt->Key[j+1]=r->Key[1];
Delete(r,1);
}
else if(l&&l->keynum>s-1)
{
int k;
for(k=i;k>1;k--)
{
v->Key[k]=v->Key[k-1];
v->recptr[k]=v->recptr[k-1];
}
v->Key[k]=pt->Key[j];
pt->Key[j]=l->Key[l->keynum];
l->keynum--;
}
else
{
for(int k=i;k<v->keynum;k++)
{
v->Key[k]=v->Key[k+1];
v->recptr[k]=v->recptr[k+1];
}
v->keynum--;
Merge(v);
}
}
return;
}
Status DeleteBTree(BTree T,KeyType K)
{
Result res=SearchBTree(T,K);
if(res.tag==0)return ERROR;
BTree v=res.pt;
int i=res.i;
if(v->ptr[0]==NULL)
{//终端节点
Delete(v,i);
}
else
{//存在于内部节点
BTree p=v->ptr[0];
while(p->ptr[0]!=NULL)p=p->ptr[0];
v->Key[i]=p->Key[1];
Delete(p,1);
}
return OK;
}
最后在main源文件中只需要包含该头文件即可使用定义的抽象数据类型:文章来源:https://www.toymoban.com/news/detail-796512.html
#include <stdio.h>
#include <stdlib.h>
#include "BTree.h"
int main()
{
printf("Hello world!\n");
return 0;
}
这里没有提供具体样例,可根据实际情况自行编写。文章来源地址https://www.toymoban.com/news/detail-796512.html
到了这里,关于B_Tree 的数据结构的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!