机器人在笛卡尔空间和关节空间的多项式轨迹规划以及matlab代码（三次、五次、七次）-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器人在笛卡尔空间和关节空间的多项式轨迹规划以及matlab代码（三次、五次、七次）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

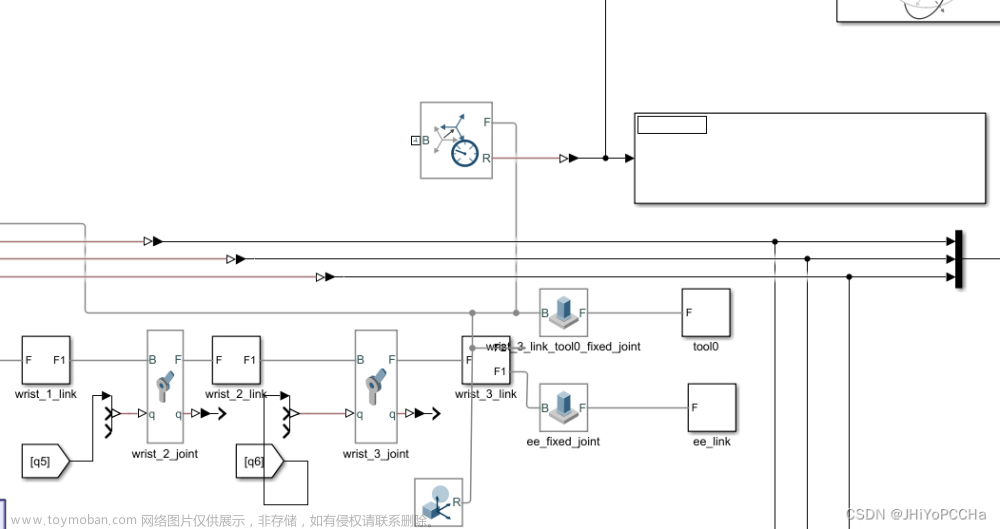
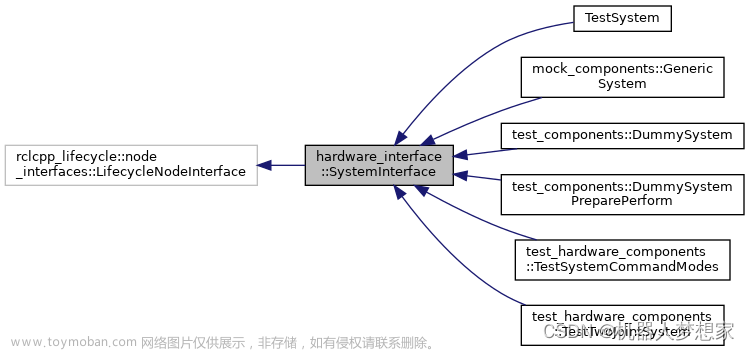
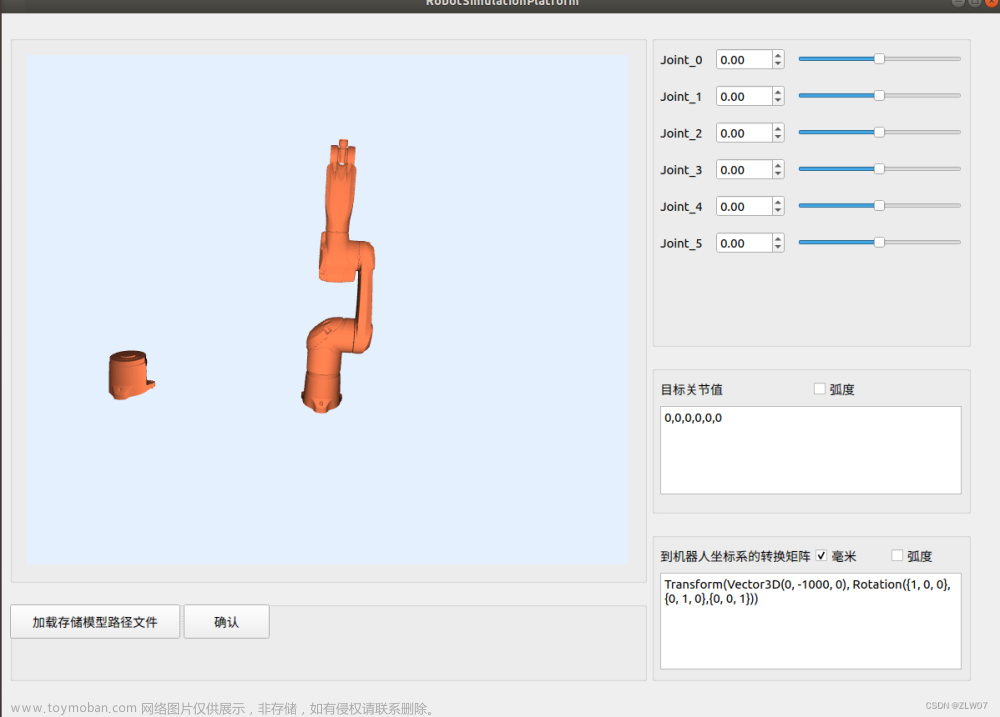
三次多项式轨迹规划：

三次多项式轨迹规划就是s(t)相对于时间t的变化满足三次多项式变化，其表达式如下：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

如前文所述：t的取值范围是[0,T],s(t)的取值范围是[0,1], 又因为初始速度和末速度都为0，所以：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

S（t）的一阶导数表达式为：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

从而可以计算出对应的系数：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

将系数带入到上面的三次多项式，可得到

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

再将上式代入到路径表达式，即可得到完整的轨迹规划表达式，如下所示：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

其中，最大的关节速度在 matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人时刻到达，其数值为：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

最大的关节加速度和关节减速度在 matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人和，其中：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

关节空间三次多项式轨迹规划：

TH1=[30,60,2,5,50,70,80]; %定义关节空间中的两个点TH1,TH2.
TH2=[90,54,3,60,80,40,60];
T=1;%定以一个时间，即从TH1到TH2的总时间。
TH=[];
TH_yijie=[];
TH_erjie=[];
TT=[];%定以四个变量TH、TH_yijie、TH_erjie、TT，用来储存数据
for t=0:0.001:T  
    th=TH1+(TH2-TH1)*(3*t^2/T^2-2*t^3/T^3);%角度和时间变化关系
    th_yijie=(TH2-TH1)*(6*t/T^2-6*t^2/T^3);%角速度和时间变化关系
    th_erjie=(TH2-TH1)*(6/T^2-12*t/T^3);%角加速度和时间变化关系
    TH=[TH,th'];
    TH_yijie=[TH_yijie,th_yijie'];
    TH_erjie=[TH_erjie,th_erjie'];
    TT=[TT,t];
end
TH=TH';%矩阵转置
TH_yijie=TH_yijie';
TH_erjie=TH_erjie';
TT=TT';
fig1=figure;
plot(TT,TH(:,1));%三维绘图此处绘制一轴关节角度变化示意。
grid on;
fig2=figure;
plot(TT,TH_yijie(:,1));%三维绘图此处绘制一轴关节角速度变化示意。
grid on;
fig3=figure;
plot(TT,TH_erjie(:,1));%三维绘图此处绘制一轴关节角加速度变化示意。
grid on;

笛卡尔空间三次多项式轨迹规划：

A=[30,60,2]; %定义笛卡尔空间中的两个点A,B.
B=[90,54,3];
T=1;%定义一个时间，即从A到B的总时间。
X=[];
X_yijie=[];
X_erjie=[];
TT=[];%定以四个变量X、X_yijie、X_erjie、TT，用来储存数据
for t=0:0.001:T  
    x=A+(B-A)*(3*t^2/T^2-2*t^3/T^3);%角度和时间变化关系
    x_yijie=(B-A)*(6*t/T^2-6*t^2/T^3);%角速度和时间变化关系
    x_erjie=(B-A)*(6/T^2-12*t/T^3);%角加速度和时间变化关系
    X=[X,x'];
    X_yijie=[X_yijie,x_yijie'];
    X_erjie=[X_erjie,x_erjie'];
    TT=[TT,t];
end
X=X';%矩阵转置
X_yijie=X_yijie';
X_erjie=X_erjie';
TT=TT';
fig1=figure;
plot(TT,X(:,1));%三维绘图此处绘制x方向位移变化示意。
grid on;
fig2=figure;
plot(TT,X_yijie(:,1));%三维绘图此处绘制x方向速度变化示意。
grid on;
fig3=figure;
plot(TT,X_erjie(:,1));%三维绘图此处绘制x方向加速度变化示意。
grid on;

五次多项式轨迹规划：

五次多项式轨迹规划就是s(t)相对于时间t的变化满足五次多项式变化，其表达式如下：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

其中：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

求出系数如下：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

所以其运动方程如下：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

各个变量的最值如下：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

关节空间五次多项式轨迹规划：

TH1=[30,60,2,5,50,70,80]; %定义关节空间中的两个点TH1,TH2.
TH2=[90,54,3,60,80,40,60];
T=1;%定以一个时间，即从TH1到TH2的总时间。
TH=[];
TH_yijie=[];
TH_erjie=[];
TT=[];%定以四个变量TH、TH_yijie、TH_erjie、TT，用来储存数据
for t=0:0.001:T  
    th=TH1+(TH2-TH1)*(10*(t/T)^3-15*(t/T)^4+6*(t/T)^5);%角度和时间变化关系
    th_yijie=(TH2-TH1)*(30*(t/T)^2-60*(t/T)^3+30*(t/T)^4);%角速度和时间变化关系
    th_erjie=(TH2-TH1)*(60*(t/T)-180*(t/T)^2+120*(t/T)^3);%角加速度和时间变化关系
    TH=[TH,th'];
    TH_yijie=[TH_yijie,th_yijie'];
    TH_erjie=[TH_erjie,th_erjie'];
    TT=[TT,t];
end
TH=TH';%矩阵转置
TH_yijie=TH_yijie';
TH_erjie=TH_erjie';
TT=TT';
fig1=figure;
plot(TT,TH(:,1));%三维绘图此处绘制一轴关节角度变化示意。
grid on;
fig2=figure;
plot(TT,TH_yijie(:,1));%三维绘图此处绘制一轴关节角速度变化示意。
grid on;
fig3=figure;
plot(TT,TH_erjie(:,1));%三维绘图此处绘制一轴关节角加速度变化示意。
grid on;

笛卡尔空间五次多项式轨迹规划：

A=[30,60,2]; %定义笛卡尔空间中的两个点A,B.
B=[90,54,3];
T=1;%定义一个时间，即从A到B的总时间。
X=[];
X_yijie=[];
X_erjie=[];
TT=[];%定以四个变量X、X_yijie、X_erjie、TT，用来储存数据
for t=0:0.001:T  
    x=A+(B-A)*(10*(t/T)^3-15*(t/T)^4+6*(t/T)^5);%角度和时间变化关系
    x_yijie=(B-A)*(30*(t/T)^2-60*(t/T)^3+30*(t/T)^4);%角速度和时间变化关系
    x_erjie=(B-A)*(60*(t/T)-180*(t/T)^2+120*(t/T)^3);%角加速度和时间变化关系
    X=[X,x'];
    X_yijie=[X_yijie,x_yijie'];
    X_erjie=[X_erjie,x_erjie'];
    TT=[TT,t];
end
X=X';%矩阵转置
X_yijie=X_yijie';
X_erjie=X_erjie';
TT=TT';
fig1=figure;
plot(TT,X(:,1));%三维绘图此处绘制x方向位移变化示意。
grid on;
fig2=figure;
plot(TT,X_yijie(:,1));%三维绘图此处绘制x方向速度变化示意。
grid on;
fig3=figure;
plot(TT,X_erjie(:,1));%三维绘图此处绘制x方向加速度变化示意。
grid on;

七次多项式轨迹规划：

五次多项式轨迹规划就是s(t)相对于时间t的变化满足五次多项式变化，其表达式如下：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

其中：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

求出系数如下：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

所以其运动方程如下：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人

各个变量的最值如下：

matlab利用三次多项式规划出关节角运动轨迹,Matlab机器人轨迹规划,机器人文章来源地址https://www.toymoban.com/news/detail-796670.html

关节空间七次多项式轨迹规划：

TH1=[30,60,2,5,50,70,80]; %定义关节空间中的两个点TH1,TH2.
TH2=[90,54,3,60,80,40,60];
T=1;%定以一个时间，即从TH1到TH2的总时间。
TH=[];
TH_yijie=[];
TH_erjie=[];
TT=[];%定以四个变量TH、TH_yijie、TH_erjie、TT，用来储存数据
for t=0:0.001:T  
    th=TH1+(TH2-TH1)*(35*(t/T)^4-84*(t/T)^5+70*(t/T)^6-20*(t/T)^7);%角度和时间变化关系
    th_yijie=(TH2-TH1)*(140*(t/T)^3-420*(t/T)^4+420*(t/T)^5-140*(t/T)^6);%角速度和时间变化关系
    th_erjie=(TH2-TH1)*(420*(t/T)^2-1680*(t/T)^3+2100*(t/T)^4-840*(t/T)^5);%角加速度和时间变化关系
    TH=[TH,th'];
    TH_yijie=[TH_yijie,th_yijie'];
    TH_erjie=[TH_erjie,th_erjie'];
    TT=[TT,t];
end
TH=TH';%矩阵转置
TH_yijie=TH_yijie';
TH_erjie=TH_erjie';
TT=TT';
fig1=figure;
plot(TT,TH(:,1));%三维绘图此处绘制一轴关节角度变化示意。
grid on;
fig2=figure;
plot(TT,TH_yijie(:,1));%三维绘图此处绘制一轴关节角速度变化示意。
grid on;
fig3=figure;
plot(TT,TH_erjie(:,1));%三维绘图此处绘制一轴关节角加速度变化示意。
grid on;

笛卡尔空间七次多项式轨迹规划：

A=[30,60,2]; %定义笛卡尔空间中的两个点A,B.
B=[90,54,3];
T=1;%定义一个时间，即从A到B的总时间。
X=[];
X_yijie=[];
X_erjie=[];
TT=[];%定以四个变量X、X_yijie、X_erjie、TT，用来储存数据
for t=0:0.001:T  
    x=A+(B-A)*(35*(t/T)^4-84*(t/T)^5+70*(t/T)^6-20*(t/T)^7);%角度和时间变化关系
    x_yijie=(B-A)*(140*(t/T)^3-420*(t/T)^4+420*(t/T)^5-140*(t/T)^6);%角速度和时间变化关系
    x_erjie=(B-A)*(420*(t/T)^2-1680*(t/T)^3+2100*(t/T)^4-840*(t/T)^5);%角加速度和时间变化关系
    X=[X,x'];
    X_yijie=[X_yijie,x_yijie'];
    X_erjie=[X_erjie,x_erjie'];
    TT=[TT,t];
end
X=X';%矩阵转置
X_yijie=X_yijie';
X_erjie=X_erjie';
TT=TT';
fig1=figure;
plot(TT,X(:,1));%三维绘图此处绘制x方向位移变化示意。
grid on;
fig2=figure;
plot(TT,X_yijie(:,1));%三维绘图此处绘制x方向速度变化示意。
grid on;
fig3=figure;
plot(TT,X_erjie(:,1));%三维绘图此处绘制x方向加速度变化示意。
grid on;

到了这里，关于机器人在笛卡尔空间和关节空间的多项式轨迹规划以及matlab代码（三次、五次、七次）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！