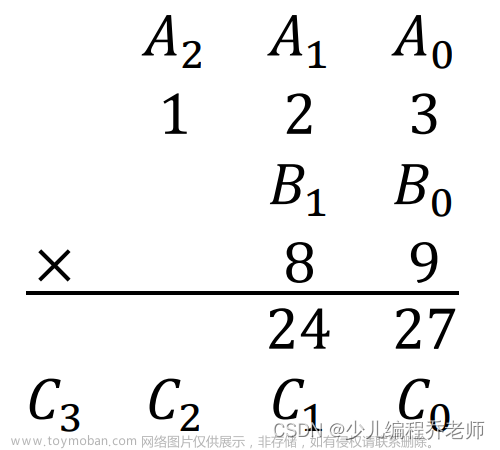高精度算法详解-Toy模板网

这篇具有很好参考价值的文章主要介绍了高精度算法详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

首先要知道为什么需要高精度算法：

高精度算法是处理大数字的数学计算方法，当数字过大不能用int和long long存储时，我们就可以使用string和vector类型来存储他们的每一位，然后进行计算。

一、高精度加法

1.1 思路

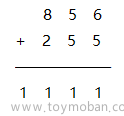
我们可以先把要输入的两个数字放到vector中存储，注意要反着存（后边做加法的时候最后有进位就可以直接push_back），接下来就是加法：
设置一个add变量表示进位，创建一个res保存每一位，add 加上两个数字，把add % 10放入res中，再把add /= 10。
在最后要注意循环完且add不为0的情况。

1.2 例题：高精度加法

题目链接

题目描述

给定两个正整数（不含前导 0），计算它们的和。

输入格式

共两行，每行包含一个整数。

输出格式

共一行，包含所求的和。

数据范围

1≤整数长度≤100000

输入样例：

12
23

输出样例：

35

#include <iostream>
#include <string>
#include <vector>

using namespace std;

vector<int> add(const vector<int>& a, const vector<int>& b)
{
    int add = 0;
    vector<int> res;
    for(int i = 0; i < a.size() || i < b.size() || add; i++)
    {
        if(i < a.size()) add += a[i];
        if(i < b.size()) add += b[i];
        res.push_back(add % 10);
        add /= 10;
    }
    return res;
}

int main()
{
    string a, b;
    cin >> a >> b;
    vector<int> A, B;
    for(int i = a.size() - 1; i >= 0; i--)
    {
        A.push_back(a[i] - '0');
    }
    for(int i = b.size() - 1; i >= 0; i--)
    {
        B.push_back(b[i] - '0');
    }
    vector<int> res = add(A, B);
    for(int i = res.size() - 1; i >= 0; i--)
    {
        printf("%d", res[i]);
    }
    return 0;
}

这里要注意最后打印结果的时候如果直接计算不管是用int或long long都不够，所以直接打印每位了。

二、高精度减法

思路分析

2.1 思路

这里要注意有可能为小 - 大，所以需要写一个判断函数来判断大小。
减法：
定义一个变量del表示借位，res存储每一位，每次del = a[i] - b[i] - del，把(del + 10) % 10push_back到res中。再判断del是否小于0，如果小于0，就令del = 1，否则del = 0。

最后还要注意消掉后置0，比如1000 - 999时（反过来存）结果就为1000，需要消掉后面的三个0。

2.2 例题：高精度减法

题目描述

给定两个正整数（不含前导 0），计算它们的差，计算结果可能为负数。

输入格式

共两行，每行包含一个整数。

输出格式

共一行，包含所求的差。

数据范围

1≤整数长度≤105

输入样例：

32
11

输出样例：

21

#include <iostream>
#include <string>
#include <vector>

using namespace std;

// a >= b ?
bool cmp(const vector<int>& a, const vector<int>& b)
{
    int n = a.size(), m = b.size();
    if(n != m)
    {
        return n >= m;
    }
    for(int i = n - 1; i >= 0; i--)
    {
        if(a[i] != b[i])
        {
            return a[i] > b[i];
        }
    }
    return true;
}

vector<int> del(vector<int>& a, vector<int>& b)
{
    if(!cmp(a, b)) return del(b, a);
    vector<int> res;
    int del = 0;
    for(int i = 0; i < a.size(); i++)
    {
        if(i < b.size()) del += b[i];
        del = a[i] - del;
        res.push_back((del + 10) % 10);
        if(del < 0) del = 1;
        else del = 0;
    }
    while(res.size() > 1 && res.back() == 0) res.pop_back();
    return res;
}

int main()
{
    string a, b;
    cin >> a >> b;
    vector<int> A, B;
    for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for(int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
    vector<int> res = del(A, B);
    if(!cmp(A, B))
    {
        printf("-");
    }
    for(int i = res.size() - 1; i >= 0; i--)
    {
        printf("%d", res[i]);
    }
    return 0;
}

三、高精度乘法

3.1 思路

用123 * 12 来举例子：
高精度算法,百炼成钢,算法,c++,c语言

这也要注意去除后置0：1000 * 0 = 0000（消掉后三个0）

3.2 例题：高精度乘法

题目描述

题目描述

给定两个非负整数（不含前导 0） A 和 B，请你计算 A×B 的值。

输入格式

共两行，第一行包含整数 A，第二行包含整数 B。

输出格式

共一行，包含 A×B 的值。

数据范围

1≤A的长度≤100000,
0≤B≤10000

输入样例：

2
3

输出样例：

6

#include <iostream>
#include <string>
#include <vector>

using namespace std;

vector<int> mul(const vector<int>& a, int b)
{
    int add = 0;
    vector<int> res;
    for(int i = 0; i < a.size() || add; i++)
    {
        if(i < a.size()) add = a[i] * b + add;
        res.push_back(add % 10);
        add /= 10;
    }
    while(res.size() > 1 && res.back() == 0) res.pop_back();
    return res;
}

int main()
{
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    vector<int> res = mul(A, b);
    for(int i = res.size() - 1; i >= 0; i--)
    {
        printf("%d", res[i]);
    }
    return 0;
}

四、高精度除法

4.1 思路

这里我们可以发现我们在做除法的时候不需要把数据逆置，但是为了保持统一，还是逆置再做除法，除法过程：
他需要返回余数，设变量r为余数， r = r * 10 + a[i]，把r / b尾插入res数组，再让r %= 10即可。
最后再把res数组逆置，消除后置0。

4.2 例题：高精度除法

题目链接

题目描述

给定两个非负整数（不含前导 0） A，B，请你计算 A/B 的商和余数。

输入格式

共两行，第一行包含整数 A，第二行包含整数 B。

输出格式

共两行，第一行输出所求的商，第二行输出所求余数。

数据范围

1≤A的长度≤100000,
1≤B≤10000,
B 一定不为 0

输入样例：

7
2

输出样例：

3
1文章来源地址https://www.toymoban.com/news/detail-796840.html

#include <iostream>
#include <string.h>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> div(const vector<int>& a, int b, int& r)
{
    vector<int> res;
    for(int i = a.size() - 1; i >= 0; i--)
    {
        r = r * 10 + a[i];
        res.push_back(r / b);
        r %= b;
    }
    reverse(res.begin(), res.end());
    while(res.size() > 1 && res.back() == 0) res.pop_back();
    return res;
}

int main()
{
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    int r = 0;
    vector<int> res = div(A, b, r);
    for(int i = res.size() - 1; i >= 0; i--)
    {
        printf("%d", res[i]);
    }
    printf("\n%d", r);
    return 0;
}