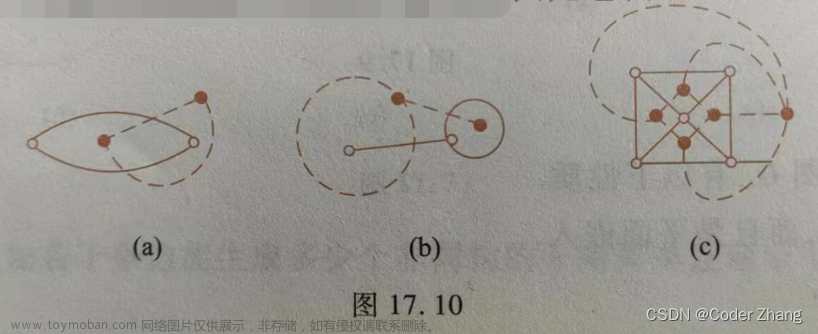
这个图就是著名的K5,有5个节点,每个节点都和其它节点全互联,构成一个5阶的完全图。
“传说”K5是最小的非平面图,也就是说,它是没法画在一个平面上,使得所有的边都能保持两两都不相交。以下一段DOT语言的代码代码可以让DOT生成一个K5。
graph link
{
node[shape="circle",color=blue];
rankdir="LR";
1;
2;
3;
4;
5;
1--2;
1--3;
1--4;
1--5;
2--3;
2--4;
2--5;
3--4;
3--5;
4--5;
}
只是长相上不太好看。但是逻辑是没有错的,因为图论中的图,只讲关系不讲位置。
它生成的结果如下,

也可以再来一个略微好看的,
graph link
{
node[shape="circle",color=blue];
rankdir="TD";
1;
2;
3;
4;
5;
1--2;
1--3;
1--4;
1--5;
2--3;
2--4;
2--5;
3--4;
3--5;
4--5;
{rank=same;2;3;}
{rank=same;4;5}
}
图像如下,

为啥这图不是平面图?
我们把它用人好理解的方式画一下就清楚了。

我们可以把K5理解为1-2-3三个顶点和顶点之间的边构成的三角形,其中心为4,4也和1,2,3都相连。然后,我们把4复制一份叫做5,它也和1,2,3都相连,并且和4也相连。我们把5从1234构成的平面上抽出来,放在高处,就是上面的样子,这个图要当成一个3D透视图来看才对。
现在考虑一下,如果5落回到1234构成的平面,有没有一种可能使得5和1,2,3,4的连线构成的边和平面上1,2,3,4互联的已有的边不相交?
当然也不是没有,正如5是4的克隆,如果5和4完全重叠那所有的边也都完全重叠,这就不叫作相交了,否则,若不重叠,怎么都会有一种相交的方式。这就是它不是平面图的原因。
但是,还是说但是,当我们给出节点和关系的时候,可从未说过空间位置上的重叠行不行的问题。也就是说,图论只考虑节点和节点之间的关系,不涉及二维还是三维空间的几何属性。所以所谓K5是非平面图的说法,恐怕又是把Graph和Image搞混了之后的结果。就像是我们用五色定理来推导四色定理,实质上两者是风马牛不相及的。
所以我认为要从图论本身检测一个Graph是不是平面图,应当是不可能的,或者不应该的。同理只用图论去论证四色问题,也是不对的。它应当还是一个平面几何问题,而不只是图论问题,至少必须是一个图论和几何的混合问题。
举一个例子,两个钥匙环环环相扣,这种情况肯定不能放在一个平面上。但是若用图论的方法将其变成节点和边的关系,我们就要面对这样一个问题:如何检测一个回路穿过了另一个回路。我们只能知道两个回路是否有连接,而是否能穿过,则是一个空间位置的问题。两个回路既可以彼此穿过,也可以相隔万里,但逻辑上来说,并无实质区别。也就是说,穿过这个词在图论中很可能是没有意义的。文章来源:https://www.toymoban.com/news/detail-797035.html
那么K5是不是非平面图,或者图论本身到底能不能检测平面图等等问题,恐怕就要仁者见仁智者见智了。文章来源地址https://www.toymoban.com/news/detail-797035.html
到了这里,关于K5 是平面图吗?的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!