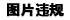了解《单链表》看这篇就好了（内含动图）！！！-Toy模板网

这篇具有很好参考价值的文章主要介绍了了解《单链表》看这篇就好了（内含动图）！！！。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

🎇🎇🎇作者：
@小鱼不会骑车
🎆🎆🎆专栏：
《java练级之旅》
🎓🎓🎓个人简介：
一名专科大一在读的小比特，努力学习编程是我唯一的出路😎😎😎

🍂顺序表的优缺点

通过前面讲到了顺序表，也可总结出线性表顺序存储结构的优缺点：
优点：

无须为表示表中元素之间的逻辑关系而增加额外的存储空间

可以快速地存取表中任一位置元素（随机读取）

缺点：

插入和删除操作需要移动大量元素

当线性表长度变化较大肘，难以确定存储空间的容量

造成存储空间的"碎片"

总结：

① 顺序表的劣势，体现在插入和删除元素方面。由于数组元素连续紧密地存储在内存中，插入、删除元素都会导致大量元素被迫移动，影响效率。
② 顺序表所适合的是读操作多、写操作少的场景。

那有没有一个能够解决这个问题的办法呢？

当然有！下面介绍到的链表就可以解决这个问题！

🍄链表的介绍（可以跳过）

一本书中是这样介绍链表的：

他说链表就像是地下党，这个地下工作者只知道自己的上级信息和自己的下级信息，如果哪天这个地下工作者的上级被敌人发现，那么就没有人能够再传递信息给这位地下工作者了，也就和上级就断了联络。就像电影《无间道》里面，梁朝伟是警方的卧底，一直是与黄秋生扮演的警察联络，可是当黄遇害后，梁就无法证明自己是个警察。所以影片的结尾，梁朝伟用枪指着刘德华的头说，"对不起，我是警察 "。刘德华马上反问道"谁知道呢? "其实这就相当于一个链式关系的现实样例。

那链表是什么样子呢？我们往下看
我们先来看一下链表的结构：
单链表的示意图,数据结构,数据结构,算法
链表（linked list）是一种在物理上非连续、非顺序的数据结构，由若干节点组成。

其实链表是有八种结构的：
单链表的示意图,数据结构,数据结构,算法
分别是上图讲到的：

单链表	双链表
带头循环单链表	带头循环双链表
带头非循环单链表	带头非循环双链表
不带头循环单链表	不带头循环双链表
不带头非循环单链表	不带头非循环双链表

当然啦，虽然有这么多的结构，其实我们只需要学会单向不带头非循环链表一个就够用，所以同学们也不要感觉这个好难！当然，这一部分还是有很大的难度的，介于基础不太好的同学可以去B站找一些相关《数据结构》的视频讲解来学习一下！

🍄链表在内存中的存储方式

如果说顺序表是以连续的方式存储，那我们就可以理解为链表是随机存储，让我们看一看下面两张图，对比一下数组和链表在内存中分配方式的不同。

顺序存储：
单链表的示意图,数据结构,数据结构,算法

随机存储：

单链表的示意图,数据结构,数据结构,算法

那么我们的链表是如何找到下一个结点的呢？

🍄定义单向链表的成员

我们需要有一个成员用来存放需要保存的数据，还需要一个成员用来存储下一个元素的地址！

public class ListNode<E> {
	//内部类
    public class Node<E> {
    //这里用到泛型是方便存储任意类型的数据
        E date;//元素
        Node next;//指针，存放下一个元素的地址
		//构造方法，在实例化这个类时直接将date的值初始化
        public Node(E date) {
           this.date=date;
        }
    }
 }

我们定义了两个成员，date是用来存放元素的，next是用来存放下一个结点的地址，并且我们还可以通过这个构造方法来初始化我的date.

注意！我们next的类型是Node的类型。并且由于后续的方法都跟这个类有关，所以我们将这个类定义为内部类！

我们来看一下单向链表的大概示意图：

单链表的示意图,数据结构,数据结构,算法
我们的next一直存放的都是下一个结点的地址，但是到了最后一个结点，由于后面没有数据，我们就可以将最后一个结点的next 置为null.

现在链表的大致形态以及出来了，但是我们该如何找到这个链表呢？这时候就需要设置一个head来存储这个链表的头结点，以后该链表的遍历或者是该链表的增删查改都需要从这个头节点开始！


 public class ListNode<E> {
	//内部类
    public class Node<E> {
    //这里用到泛型是方便存储任意类型的数据
        E date;//元素
        Node next;//指针
		//构造方法，在实例化这个类时直接将date的值初始化
        public Node(E date) {
           this.date=date;
        }
    }
    //定义一个头节点
    public Node head;
 }

注意！

我们的头节点是外部类的成员变量，因为后续的方法在外部类中实现，如果我们将头节点定义到内部类中，那么每次实例化一个内部类就都会初始化我的头节点，这是不可以的！！！

当我们定义了这么一个类，我们首先考虑的是，如何遍历这个链表！

🍄遍历单链表

由于我们还没有实现单链表的增删查改所以我们先通过自己手动实例化来创建结点！

    public static void main(String[] args) {
        ListNode<Integer> listNode=new ListNode<>();
        ListNode.Node<Integer> p1=new ListNode.Node<>(20);
        ListNode.Node<Integer> p2=new ListNode.Node<>(30);
        ListNode.Node<Integer> p3=new ListNode.Node<>(40);
        listNode.head=p1;//将p1置为头节点
        p1.next=p2;//将p2的地址存入p1.next
        p2.next=p3;//将p3的地址存入p2.next    
    }

然后将我们的头节点设为p1,通过p1.next=p2存入p2结点的地址，再通过p2.next=p3来存入p3结点的地址,这时候我们的链表是这个样子的。

单链表的示意图,数据结构,数据结构,算法
那么，此时我们的链表创建好了，接下来就是打印单链表。

🍂打印单链表

此时我们想要打印单链表，那么就需要将单链表从头遍历到末尾，这说明我们需要一个while循环来控制，那么退出条件是什么呢？我们思考一下。

在我们打印完第一个结点之后，就需要打印第二个结点，那么如何找到第二个结点呢？我们可以通过第一个结点的next来找到,所以我们在打印完第一个结点之后，就可以通过head=head.next来将第二个结点的地址赋值给head，这时候我们打印head.date打印的就是第二个结点的数据，就这样一直往下，如下图

单链表的示意图,数据结构,数据结构,算法

那我们此时知道了如何向后遍历，那我们退出循环的条件是什么呢？大家可以看到，当我们的head为null时，该链表才一个结点也没有了，也就没有需要打印的了，所以我们的循环条件就是while(head!=null)，完整的代码就是，

    //打印单链表
    public void display() {
        while (head!=null) {
            System.out.print(head.date+"->");
            head=head.next;
        }
        System.out.println("null");
    }

当我们运行之后：

单链表的示意图,数据结构,数据结构,算法

是不是感觉好简单，我们接着往下看！

单链表的示意图,数据结构,数据结构,算法

这时候就有小伙伴有疑问了，为啥什么都没有打印（null是我的打印方法自带的）,我们再回过头来看这个图。

单链表的示意图,数据结构,数据结构,算法
你发现了什么？头没了，头找不到了！！！头都丢了自然下一次的打印是什么都没有，那么该如何解决呢？

       //打印单链表
    public void display() {
        Node cur=head;
        while (cur!=null) {
            System.out.print(cur.date+"->");
            cur=cur.next;
        }
        System.out.println("null");
    }

我们利用一个变量存下这个头节点，利用这个变量去遍历，这样我们修改的就是这个变量的值，而不是头结点的位置，具体过程如下：

单链表的示意图,数据结构,数据结构,算法

由于单链表的结构中没有定义表长，所以不能事先知道要循环多少次，因此也就不方便使用 fo 来控制循环。其主要核心思想就是 "工作指针后移"这其实也是很多算法的常用技术。

——《大话数据结构》

🍂获取单链表的长度

那么如何遍历链表我们以及掌握了，获取链表的长度其实就通过创建一个遍历count,每次cur在向后移时，我们的count就加一，直到我们的cur==null时退出循环代码如下：

    //得到单链表的长度
  public int size() {
      Node cur=head;
      int count=0;
      while (cur!=null) {
            count++;
            cur=cur.next;
        }
     return count;
   }

🍂找到单链表中指定结点对应的数据

经过了前面两个的学习，大家以及差不多了解了链表的遍历，那么链表的遍历学会了，我们是不是可以通过遍历链表来找到指定位置对应的结点。

查找结点：
在查找元素时，链表不像数组那样可以通过下标快速进行定位，只能从头节点开始向后一个一个节点逐一查找。

例如给出一个链表，需要查找从头节点开始的第3个节点。

单链表的示意图,数据结构,数据结构,算法

第1步，将查找的指针定位到头节点。

单链表的示意图,数据结构,数据结构,算法

第2步，根据头节点的next指针，定位到第2个节点。

单链表的示意图,数据结构,数据结构,算法

第3步，根据第2个节点的next指针，定位到第3个节点，查找完毕。

单链表的示意图,数据结构,数据结构,算法

我们也可以通过图片知道，因为链表是顺序访问的，所以查找指定结点的最坏复杂度是O(n)。

代码如下：

//index要查找的结点的位置
    public Node Find(int index) {
        Node cur=head;
        //当我的cur==null时退出循环
        while (index>0&&cur!=null) {
            cur=cur.next;
            index--;
        }
        //当cur==null时index还没有走完，说明要查找的结点不存在
        //或者当index为小于0的值时也不存在该节点，返回null
        if(cur==null||index<0) {
           return null;
        }
        return cur;
    }

🍂更新单链表中的数据

当我们想要将第三个结点的值改为888时，如图

单链表的示意图,数据结构,数据结构,算法

这个就是在之前的查找的基础上，将返回的结点的data修改，实现的化只需要两步：

    //修改单链表中指定的结点
    public void revise(int index,E val) {
    //调用单链表查找方法
        Node cur=Find(index);
        //如果返回值为null则说明没找到，直接返回
        if (cur==null) {
            return;
        }
        cur.date=val;
    }

🍄插入结点

🍂头插

什么是头插呢？就是将新开辟的结点的next指向原来链表的头，然后再重新让head称为头结点。
单链表的示意图,数据结构,数据结构,算法
代码如下：

    public void addFirst(E date) {
    //创建一个新结点，通过调用Node的构造方法初始化这个结点的date
        Node<E> node=new Node<>(date);
        //将新节点的next指向head
        node.next=head;
        //将head重新置为头节点
        head=node;
    }

🍂尾插

尾插就是将链表的最后一个结点的next指向新建的结点。

单链表的示意图,数据结构,数据结构,算法
注意，我们尾插的前提是该链表存在结点，如果该链表不存在结点，我们的cur.next就会产生空指针异常，所以如果是该链表为空链表，那么我们直接将head置为node，然后直接返回，如果不是头节点，就需要遍历，遍历到链表的最后一个结点，然后让该结点的next指向node.
代码如下：

    //尾插法
    public void addLast(E data) {
       Node<E> node=new Node<>(data);
       //判断有没有结点
       if (head==null) {
           head=node;
           return;
       }
       Node cur=head;
       //找到最后一个结点
       while (cur.next!=null) {
           cur=cur.next;
       }
       cur.next=node;
    }

🍂指定插入

指定插入就是根据我输入的结点位置来进行插入，但是由于我们是单链表，如果我想在一个链表的第3个位置插入一个结点，

单链表的示意图,数据结构,数据结构,算法

我就需要找到该链表的第二个结点，然后让node.next指向第二个结点的cur.next，最后将第二个结点的cur.next=node,将cur的next指向新节点.

如图：

单链表的示意图,数据结构,数据结构,算法

总共需要两步node.next=cur.next ;cur.next=node,那我们可不可以将这两个的顺序修改一下呢？

我们用这个图举例

单链表的示意图,数据结构,数据结构,算法

如果先cur.next=node,再node.next=cur.next,那么就会发生找不到curNext这个结点了，因为它去自己指向自己了，请看

单链表的示意图,数据结构,数据结构,算法

这样的插入操作就是失败的，造成了临场掉链子的尴尬局面。所以这两句是无论如何不能反的，这点大家一定要注意。

单链表第index位置插入结点的算法思路:

声明一个结点cur指向链表第1个结点，初始化 count从1开始.
count<index-1 时，就遍历链表，让cur的指针向后移动，不断指向下一结点，count累加1;
若到链表末尾cur为空，则说明第index个元素不存在
否则查找成功，在系统中生成一个空结点 node;
通过构造方法将node.date初始化
单链表插入的标准语句node.next=cur.next ;cur.next=node

实现代码如下：

    public void addIndex(int n,E date) {
        int count=1;//结点从1开始，数组从0开始
 		Node cur=head;
 		//因为要找到前一个位置的结点，所以循环条件是count<index-1
        while(count<n-1&&cur!=null) {
     		cur=cur.next;
            count++;
       }
       //当cur为空时说明index超出链表长度,
       //当count>index时，说明index是一个小于1的值是一个非法的位置
       if(cur==null||count>n) {
			return;
       }
       //当判断要插入的位置存在时，则创建这个结点    	
       Node node=new Node(date);
       node.next=cur.next;
       cur.next=node;
    }

🍄删除结点

单链表的删除，其实就是让要删除结点的前一个结点的指针直接指向要删除的结点的后一个结点，绕过这个结点，这样我们就再也找不到这个结点了。

单链表的示意图,数据结构,数据结构,算法

我们要做的实际上只有一步，就是让prev.next=cur.nex,也可以写为prev.next=prev.next.next,

在《大话数据结构》中是这么举例的：

打个形象的比方，本来是爸爸左手牵着妈妈的手，右手牵着宝宝的左手在马路边散步。突然迎面走来一个美女，爸爸一下子看呆了，此情此景被妈妈发现，妈妈生气的甩开牵着爸爸的手，拉起宝宝的左手就快速向前走去
单链表的示意图,数据结构,数据结构,算法

此时妈妈是prev结点，爸爸是cur结点，宝宝的结点是cur.next,当妈妈去牵宝宝的手时，这时候就跟爸爸没有牵手联系了。

单链表第index位置删除结点的算法思路：

1.声明一个结点prev指向链表第1个结点count初始化1开始。
2.当count<n-1时，就遍历链表，让prev的指针向后移动，不断指向下一个结点，count的值+1。
3.若到链表末尾prev为空，则说明第n个元素不存在;
4.否则查找成功，此时prev的next就是要删除的结点，令cur=prev.next,再让prev.next=cur.next。

实现代码算法如下：

   //指定删除结点
    public void delete(int n) {
        Node prev=head;
        //删除头节点
        if (index==1) {
            head=head.next;
            return;
        }
        int count=1;
        //当我的prev.next==null时说明我已经是最后一个结点，意味着没有找到要删除的结点
        while (prev.next!=null&&count<n-1) {
            count++;
            prev=prev.next;
        }
        if (prev.next==null||count>n) {
            return;
        }
        //要删除的结点
        Node cur=prev.next;
        //绕过要删除的结点，指向要删除的结点的下一个结点
        prev.next=cur.next;

    }

分析一下刚才讲到的链表插入和删除的方法，可以分为两部分:

第一部分就是遍历查找第n个元素
第二部分就是插入和删除元素。

总结：

从整个算法来说，我们很容易推导出:他们的时间复杂度都是 O(n) 。如果在我们不知道第n个元素的指针位置，单链表的数据结构在插入和删除操作上，与线性表的顺序存储结构是没有太大优势的。但如果，我们希望从第i个位置，插入10个元素，对于顺序存储结构意味着，每一次插入都需要移动n-i个元素，每次都是 O(n) 。而单链表，我们只需要在第一次时，找到第i个位置的指针，此时为O(n) 接下来只是简单地通过赋值移动指针而已，时间复杂度都是 O(1) 。显然对于插入或删除数据越频繁的操作，单链表的效率优势就越是明显。
文献来自—《大话数据结构》