背景
什么是隐私
讲差分隐私前,说一下什么是隐私
其实隐私这个定义,各家有各家的说法,而且各人有各人不同的考量。目前普遍比较接受的是:“单个用户的某一些属性” 可以被看做是隐私。这个说法里所强调的是:单个用户。也就是说,如果是一群用户的某一些属性,那么可以不看做隐私。
举个例子:医院说,抽烟的人有更高的几率会得肺癌。这个不泄露任何隐私。但是如果医院说,张三因为抽烟,所以有了肺癌。那么这个就是隐私泄露了。好,那么进一步,虽然医院发布的是趋势,说抽烟的人更高几率得肺癌。然后大家都知道张三抽烟,那么是不是张三就会有肺癌呢?那么这算不算隐私泄露呢?结论是不算,因为张三不一定有肺癌,大家只是通过一个趋势猜测的。
所以,从隐私保护的角度来说,隐私的主体是单个用户,只有牵涉到某个特定用户的才叫隐私泄露,那么我们是不是可以任意发布聚集信息呢?倒是未必。我们设想这样一种情况:医院发布了一系列信息,说我们医院这个月有100个病人,其中有10个感染HIV。假如攻击者知道另外99个人是否有HIV的信息,那么他只需要把他知道的99个人的信息和医院发布的信息比对,就可以知道第100个人是否感染HIV。这种对隐私的攻击行为就是差分攻击。
差分隐私
差分隐私顾名思义就是用来防范差分攻击的。举个简单的例子,假设现在有一个婚恋数据库,2个单身8个已婚,只能查有多少人单身。刚开始的时候查询发现,2个人单身;现在张三跑去登记了自己婚姻状况,再一查,发现3个人单身,所以张三单身。
从群里数据通过差分攻击(查询的方式)推测个体隐私。
差分隐私(Differential Privacy)是Dwork 在2006年针对数据库的隐私泄露问题提出的一种新的隐私定义。主要是通过使用随机噪声来确保,查询请求公开可见信息的结果,并不会泄露个体的隐私信息,即提供一种当从统计数据库查询时,最大化数据查询的准确性,同时最大限度减少识别其记录的机会,简单来说,就是保留统计学特征的前提下去除个体特征以保护用户隐私。
怎么实现差分隐私呢,简单的说就是向数据中加入噪声。但差分隐私的优势就在于这个噪声并不是随便加的,而是通过数学方法得到一个平衡,通过对差分隐私参数的调节,可以让用户在隐私保护强度和数据可用性之间寻求一个合适的平衡点。
为了更好的理解差分隐私的定义,这里先介绍一些关于信息量和熵的知识。
KL散度
KL散度(Kullback Leible-Divergence)概念来源于概率论与信息论,又被称作相对熵、互熵。从统计学意义上来说,KL散度可以用来衡量两个分布之间的差异程度,差异越小,KL散度越小。
信息量
任何事件都会承载着一定的信息量,包括已经发生的事件和未发生的事件,只是它们承载的信息量会有所不同。如昨天下雨这个已知事件,因为已经发生,既定事实,那么它的信息量就为0。如明天会下雨这个事件,因为未有发生,那么这个事件的信息量就大。
从上面例子可以看出信息量是一个与事件发生概率相关的概念,而且可以得出,事件发生的概率越小,其信息量越大。这也很好理解,狗咬人不算信息,人咬狗才叫信息嘛。
我们已知某个事件的信息量是与它发生的概率有关,那我们可以通过如下公式计算信息量:


熵
信息论中熵定义首次被香农提出:无损编码事件信息的最小平均编码长度。通俗理解,如果熵比较大,即对该信息进行编码的最小平均编码长度较长,意味着该信息具有较多可能的状态,即有着较大的信息量/混乱程度/不确定性。从某种角度上看,熵描述了一个概率分布的不确定性。总之,熵就是信息量的期望。

KL散度
用来衡量也是两个随机分布之间距离的度量

另外需要注意的是

最大散度
KL散度是从整体上衡量两个分布的距离,最大散度是两个分布比值的最大值,从两个分布比值的最大值角度衡量了两个分布的差异

差分隐私
定义
对于任意两个相邻数据集D,D',如果有一个随机化算法M 满足以下条件,则可以认为该算法满足差分隐私。

其中,默认

可以简单理解上述定义:在两个相邻数据集上,算法获得同一个集合中输出结果的概率相差不大。其中相差不大的定义则通过隐私预算参数调节,隐私预算越小,对两个数据集输出结果的限制就越小,保护隐私的程度就越强。
差分隐私的公式可以转化为

上面描述的是严格的差分隐私的定义,为了算法的实用性,Dwork后面引入了松弛的差分隐私,加入一个小常数(称作失败概率)。允许普通的 ϵ -DP 以概率 δ (最好小于 1/|d| )被打破的可能性。

定义的由来
差分隐私的目的是使经差分隐私算法处理过后的两个相邻数据集的分布尽可能接近,我们可以用最大散度衡量两个分布的差异。

常用的随机化机制有:
-
拉普拉斯机制(Laplace mechanism)
-
指数机制(Exponential mechanism)
-
高斯机制(Gaussian mechanism)
敏感度
对于相邻数据集D,D′,对于一个随机化函数M:M的敏感度为接收所有可能的输入后,得到输出的最大变化值:

其中,‖⋅‖表示向量的范数。L1敏感度和L2敏感度分别适用于L1范数和L2范数。
上述的是局部敏感度,全局敏感度就是最大的局部敏感度。
联邦学习与差分隐私
高斯噪声机制
逼近确定性实值函数的一种常见范例:f:d→R 的一个常见范例是通过加性噪声对函数 f 的灵敏度进行校准达到 sensitivity Sf ,其灵敏度定义为 d 和 d′ 为相邻输入的绝对距离 |f(d)−f(d′)| 的最大值。例如,高斯噪声机制就是向数据中加入满足均值为0,标准差为σ的高斯噪声。其中σ的选择是比较关键的,通常:

与此同时要求

敏感度为:

基于差分隐私的联邦学习隐私保护方法
目的

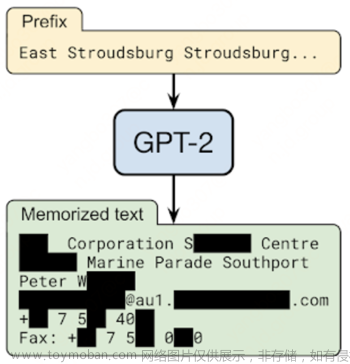
有研究表明,联邦学习中恶意参与方或服务器可以通过客户端本地模型更新中推测出客户端本地数据的属性以及时候存在某条数据等隐私信息(属性推理攻击,成员推理攻击,模型反演攻击等等)。为了保护客户端数据的隐私,可以通过差分隐私方法对本地模型参数进行模糊化处理,使恶意参与方或者中心服务器无法推理出用户的隐私且能完成模型训练的功能。
算法

为什么裁剪
敏感度是差分隐私算法非常重要的参数,而且通过上面对高斯机制的讲解,我们也发现敏感度是生成对应噪声的重要参数。为了确定全局敏感度,我们必须对模型参数进行裁剪,推导过程如下:

σ计算
如果对于σ的计算完全按照上述高斯噪声机制的计算法方法,则对于深度学习来说,相当于每个batch满足

级别的差分隐私,而对于整个数据集来说将满足

也就是更严格的差分隐私条件,显然这是不合理的。论文《Deep Learning with Differential Privacy》的解决方案是将σ写成如下形式

联邦学习方法对其进行简单的改动即可

参考文献
差分隐私(Differential Privacy)定义及其理解 - MaplesWCT - 博客园
交叉熵、相对熵(KL散度)、JS散度和Wasserstein距离(推土机距离) - 知乎
Abadi M, Chu A, Goodfellow I, et al. Deep learning with differential privacy[C]//Proceedings of the 2016 ACM SIGSAC conference on computer and communications security. 2016: 308-318.文章来源:https://www.toymoban.com/news/detail-797695.html
Wei K, Li J, Ding M, et al. Federated learning with differential privacy: Algorithms and performance analysis[J]. IEEE Transactions on Information Forensics and Security, 2020, 15: 3454-3469.文章来源地址https://www.toymoban.com/news/detail-797695.html
到了这里,关于隐私保护联邦学习之差分隐私原理的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!