稀疏矩阵的加法和乘法（三元组）-Toy模板网

这篇具有很好参考价值的文章主要介绍了稀疏矩阵的加法和乘法（三元组）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

基本思路：

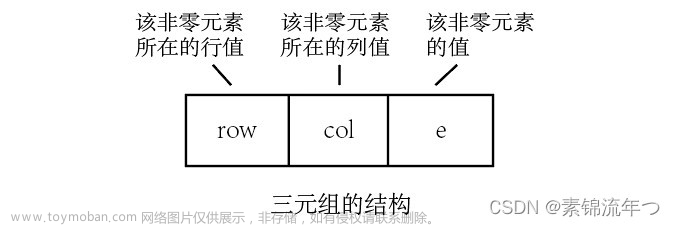
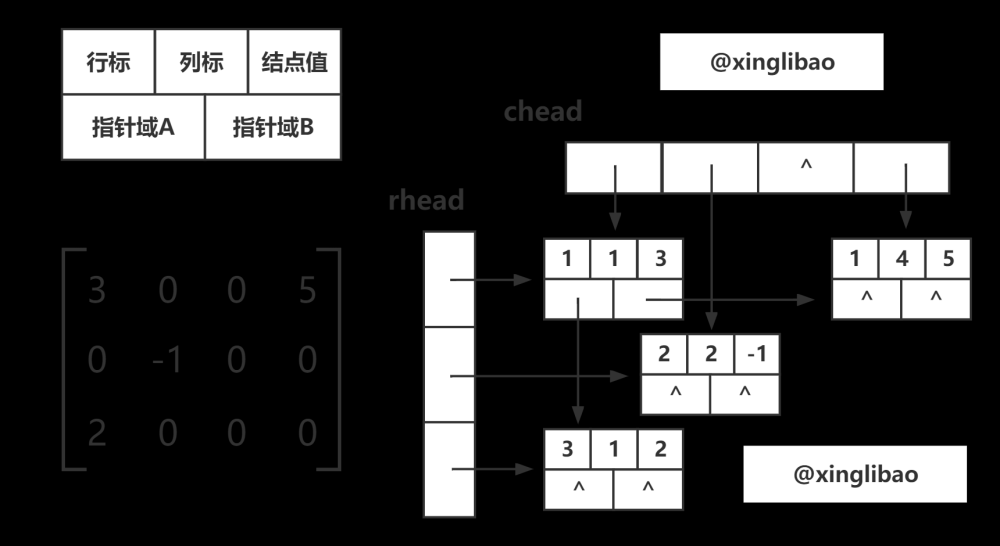
三元组方法：主要的特点就是最后的结果矩阵均由三元组的形式来表达，调用函数再以矩阵形式输出

（1）稀疏矩阵加法

（下图参考懒猫老师《数据结构》课程相关笔记）

稀疏矩阵的乘法,数据结构初步,c语言,数据结构,算法

这里与普通矩阵加法不同的是，稀疏矩阵的三元组在加法计算时，如果两个矩阵中的元素相加不为0时，才调用添加元素函数添加到和矩阵三元组中（最后的和矩阵也是一个三元组）

（2）稀疏矩阵乘法

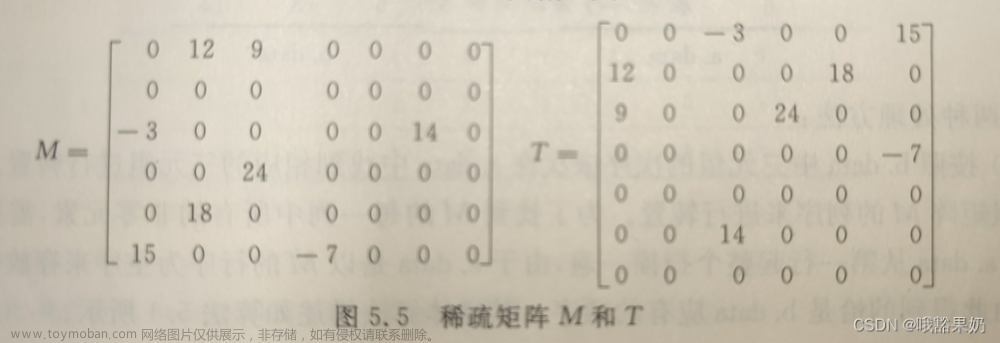
稀疏矩阵的乘法,数据结构初步,c语言,数据结构,算法

同样，在进行稀疏矩阵的乘法运算时，计算结果矩阵的元素时，要前两个矩阵在该位置的和不为0，才调用添加元素函数添加到结果矩阵三元组中

完整代码：

（稀疏矩阵（顺序）.h--用来实现稀疏矩阵的基本操作和加乘功能；稀疏矩阵加乘.c--用来对稀疏矩阵的加乘操作进行验证）

（1）稀疏矩阵（顺序）.h

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define MAX 100
typedef int DataType;

typedef struct Triple {
	int row, col; //行号，列号
	DataType item;//非零元素
} Triple;

typedef struct Matrix {
	int num;//非零元素的个数
	int mu;//矩阵的行数
	int nm;//矩阵的列数
} Matrix;

void TripleMatrix(Triple *data) { //初始化
	for (int i = 0; i < MAX; i++) {
		data[i].row = -1;
		data[i].col = -1;
	}
}

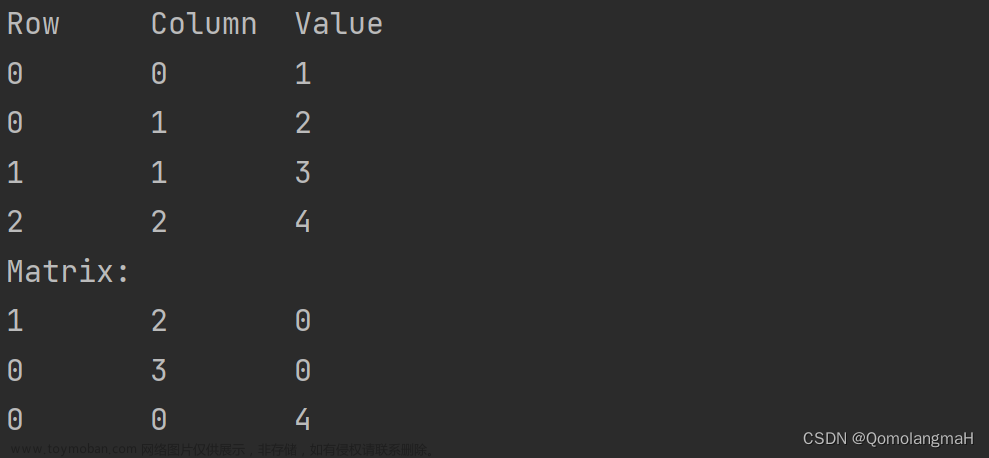
void printTriple(Triple *data) { //打印三元组
	int i = 0;
	printf("生成的三元组为：（行，列，非零元素）\n");
	while (data[i].row != -1) {
		printf("(%d，%d，%d)\n", data[i].row, data[i].col, data[i].item);
		i++;
	}
}

void printfMatrix(Triple *data, Matrix *datasum) { //打印矩阵
	printf("矩阵为：\n");
	int matirx[datasum->mu][datasum->nm];
	for (int i = 0; i < datasum->mu; i++) { //先将矩阵初始化为全0阵
		for (int j = 0; j < datasum->nm; j++) {
			matirx[i][j] = 0;
		}
	}
	for (int k = 0; k < datasum->num; k++) { //将稀疏矩阵中的值赋进去
		matirx[data[k].row - 1][data[k].col  - 1] = data[k].item; //行列值记得减1
	}
	for (int i = 0; i < datasum->mu; i++) { //打印
		for (int j = 0; j < datasum->nm; j++) {
			if (j == datasum->nm - 1)
				printf("%-5d\n", matirx[i][j]);
			else
				printf("%-5d ", matirx[i][j]);
		}
	}
}

void setItem(Triple *data, int row, int col, DataType item) { //添加元素
	Triple *str = data;
	Triple temp, temp1;
	int flag = 1; //控制两种储存交替进行
	int type = 0; //控制最后一个插入的是新元素还是原来存在temp和temp1中的元素
	while (str->row != -1 || str->col != -1) {
		if (str->row > row || (str->row == row && str->col > col)) { //插在前面
			temp = *str;
			str->row = row;
			str->col = col;
			str->item = item;
			str++;
			while (str->row != -1) {
				if (flag == 1) {
					temp1 = *str;
					*str = temp; //temp准备存储下一个
					str++;
					flag = 2;
				} else if (flag == 2) {
					temp = *str;
					*str = temp1; //temp1准备存储下一个
					str++;
					flag = 1;
				}
			}
			if (flag == 1) //最后一个元素在temp中
				type = 1;
			else if (flag == 2) //最后一个元素在temp1中
				type = 2;
		} else if (str->row < row || str->row == row) {
			str++;
		}
	}
	//前面都没有添加进去，就添加到末尾
	//或者存入temp或temp1中的需要在最后添加进去
	if (type == 0) {
		str->col = col;
		str->row = row;
		str->item = item;
	} else if (type == 1) {
		*str = temp;
	} else if (type == 2) {
		*str = temp1;
	}
}

DataType getItem(Triple *data, int row, int col, Matrix *datasum) { //根据行号列号获取矩阵元素
	if (row > datasum->mu || col > datasum->nm)
		printf("该坐标不在矩阵内！\n");
	for (int i = 0; i < datasum->num; i++) {
		if (data[i].row == row && data[i].col == col)
			return data[i].item;
	}
	return 0;
}

void addMatrix(Triple *data1, Triple *data2, Matrix *datasum1, Matrix *datasum2, Triple *add,
               Matrix *addsum) {//这个传参是真的无语
	if (datasum1->mu != datasum2->mu || datasum1->nm != datasum2->nm) {//不满足加法法则
		printf("violation of calculation rules!\n");
	}
	DataType item;
	addsum->num = 0;
	addsum->mu = datasum1->mu;
	addsum->nm = datasum1->nm;
	for (int i = 0; i < datasum1->mu; i++) {
		for (int j = 0; j < datasum1->nm; j++) {
			item = getItem(data1, i + 1, j + 1, datasum1) + getItem(data2, i + 1, j + 1, datasum2);
			if (item != 0) {//不是零就加入新的三元组中
				setItem(add, i + 1, j + 1, item);
				addsum->num++;
			}
		}
	}
}

void mulMatrix(Triple *data1, Triple *data2, Matrix *datasum1, Matrix *datasum2, Triple *mul, Matrix *mulsum) {
	if (datasum1->nm != datasum2->mu) { //不满足乘法法则
		printf("violation of calculation rules!\n");
	}
	mulsum->mu = datasum1->mu;
	mulsum->nm = datasum2->nm;
	mulsum->num = 0;
	int sum;
	for (int i = 0; i < datasum1->mu; i++) { //换第一个矩阵行
		for (int j = 0; j < datasum2->nm; j++) { //换第二个矩阵列
			sum = 0;
			for (int k = 0; k < datasum2->mu; k++) { //换第二个矩阵行
				sum += getItem(data1, i + 1, k + 1, datasum1) * getItem(data2, k + 1, j + 1, datasum2);
			}
			if (sum != 0) {//不是零就加入新的三元组中
				setItem(mul, i + 1, j + 1, sum);
				mulsum->num++;
			}
		}
	}
}

（2）稀疏矩阵加乘.c

#include "稀疏矩阵（顺序）.h"

main() {
	Triple data1[MAX];
	TripleMatrix(data1);
	Triple data2[MAX];
	TripleMatrix(data2);
	Matrix datasum1;
	Matrix datasum2;
	printf("请输入第1个矩阵初始的行，列和非零元个数：");
	scanf("%d %d %d", &datasum1.mu, &datasum1.nm, &datasum1.num);
	initMatrix(data1, datasum1.num);
	printf("请输入第2个矩阵初始的行，列和非零元个数：");
	scanf("%d %d %d", &datasum2.mu, &datasum2.nm, &datasum2.num);
	initMatrix(data2, datasum2.num);
	printf("请确认您的输入：\n");
	printf("第1个");
	printfMatrix(data1, &datasum1);
	printf("第2个");
	printfMatrix(data2, &datasum2);
	printf("如果要进行相加操作，请输入1;如果要进行相乘操作，请输入2:");
	int type;
	scanf("%d", &type);
	if (type == 1) {
		Triple add[MAX];
		TripleMatrix(add);
		Matrix addsum;
		addMatrix(data1, data2, &datasum1, &datasum2, add, &addsum);
		printf("相加后矩阵为：\n");
		printfMatrix(add, &addsum);
	} else if (type == 2) {
		Triple mul[MAX];
		TripleMatrix(mul);
		Matrix mulsum;
		mulMatrix(data1, data2, &datasum1, &datasum2, mul, &mulsum);
		printf("相乘后矩阵为：\n");
		printfMatrix(mul, &mulsum);
	}
}

void initMatrix(Triple *data, int num) {
	int row, col;
	DataType item;
	for (int i = 0; i < num; i++) { //乱序的，不用从大到小
		printf("请依次输入行，列和非零元：");
		scanf("%d %d %d", &row, &col, &item);
		setItem(data, row, col, item);
	}
}

（3）测试输出

稀疏矩阵的乘法,数据结构初步,c语言,数据结构,算法