本文将从实例的角度出发讲解fft函数的基本使用,不包含复杂的理论推导。
一、基本条件
要对一个信号进行频谱分析,首先需要知道几个基本条件。
- 采样频率fs
- 信号长度N(信号的点数)
采样频率fs:根据采样定理可知,采样频率应当大于等于被测信号里最高频率的2倍,才能保证不失真,但是实际情况下,我们可能并不知道最高频率是多少,所以这个就是根据一定的经验或者搜索得到的,比如本次所使用到的ECG(心电)信号,最高频率一般不高于100Hz,于是我们设置采样频率为500(原本200Hz就够了,但是实际工程一般会将标准放大3~5倍,以便留有一定的裕量)。
信号长度N:这个一般很容易获得,因为我们经过采样得到的信号都是离散信号,如果是一维的,只需要使用len函数就可以直接获得信号的点数。
二、设计代码实例
在Python的第三方库文件中,numpy和scipy都有fft的函数,本文使用scipy中的fft函数。
from scipy.fftpack import fft打开fft函数的源文件,可以看到如下内容:
def fft(x, n=None, axis=-1, overwrite_x=False):
"""
Return discrete Fourier transform of real or complex sequence.
The returned complex array contains ``y(0), y(1),..., y(n-1)``, where
``y(j) = (x * exp(-2*pi*sqrt(-1)*j*np.arange(n)/n)).sum()``.
Parameters
----------
x : array_like
Array to Fourier transform.
n : int, optional
Length of the Fourier transform. If ``n < x.shape[axis]``, `x` is
truncated. If ``n > x.shape[axis]``, `x` is zero-padded. The
default results in ``n = x.shape[axis]``.阅读一下可以得到输入参数的信息:
x:待进行FFT的信号序列。
n:可选,傅里叶变换的点数,如果n的长度小于序列x长度,则x将会被截断(truncated),如果n大于序列长度,则序列将会补零,默认是两者相等。
于是,我们开始对fft函数根据自己的需要进行函数封装编写:
def FFT(Fs, data):
"""
对输入信号进行FFT
:param Fs: 采样频率
:param data:待FFT的序列
:return:
"""
L = len(data) # 信号长度
N = np.power(2, np.ceil(np.log2(L))) # 下一个最近二次幂,也即N个点的FFT
result = np.abs(fft(x=data, n=int(N))) / L * 2 # N点FFT
axisFreq = np.arange(int(N / 2)) * Fs / N # 频率坐标
result = result[range(int(N / 2))] # 因为图形对称,所以取一半
return axisFreq, result代码解读:
L是输入序列的长度,很容易理解并获得。
N为大于序列长度的第一个2的幂次数,比如3之后第一个2的幂次数为,5之后的第一个2的幂次数为,因为FFT变换一般选择2的幂次进行,但是计算机计算的话,我们也可以不必如此费事,反正不是我们自己手算。
傅里叶变换的核心代码在第三行,abs是取模运算,因为FFT返回的数据是复数,为了便于绘图,需要求模进行,至于为什么后面又除以L又乘以2,是为了保证变换前后的幅值和变换前一致,比如的信号,如果不进行这一步的话,得到的FFT结果在频率为1的那个“柱子”幅度就不是2,而是一个很大的数,会发生变化,至于为什么,这里理论不去深究。
第四行代码时获取绘图所用的频率x轴,Fs/N是频率分辨率,乘以N个点就可以获得一个序列,这个序列就是每个频率分布点的x轴坐标点,N/2是为了截取一半,我们知道FFT绘制出来的图形是左右对称的,因此这里只取前一半,下面一行代码也是一样,取前一半。
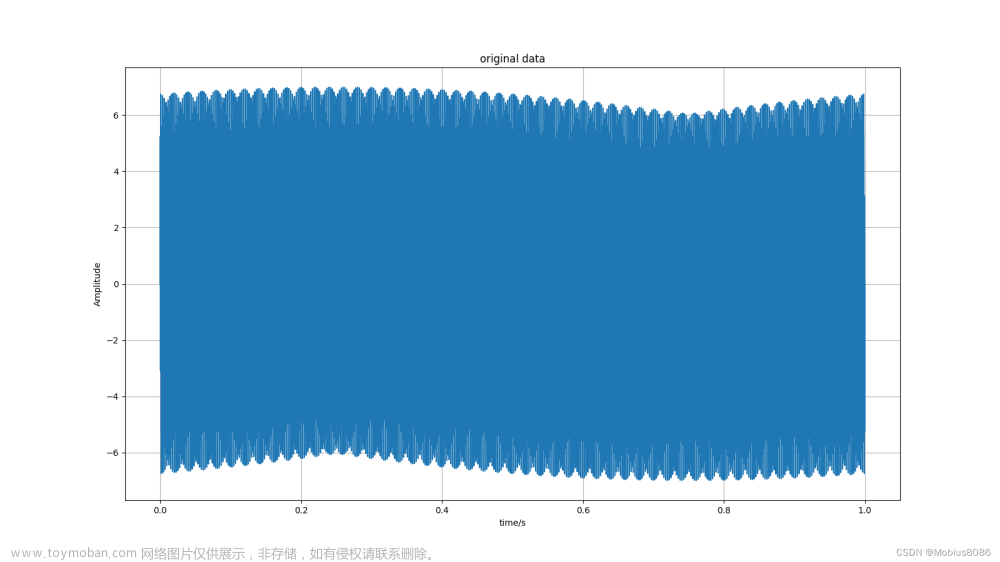
举例说明:通过手动设计被测信号和采样频率等条件,掌握对库函数fft的使用和理解,以便迁移到实际工程中。下面这个例子中,我们设计了一个信号频率为390和2000Hz的正弦叠加信号,该信号的样子如图1所示,对其进行FFT之后如图2所示。
import numpy as np
from scipy.fftpack import fft
import matplotlib.pyplot as plt
def FFT(Fs, data):
"""
对输入信号进行FFT
:param Fs: 采样频率
:param data:待FFT的序列
:return:
"""
L = len(data) # 信号长度
N = np.power(2, np.ceil(np.log2(L))) # 下一个最近二次幂,也即N个点的FFT
result = np.abs(fft(x=data, n=int(N))) / L * 2 # N点FFT
axisFreq = np.arange(int(N / 2)) * Fs / N # 频率坐标
result = result[range(int(N / 2))] # 因为图形对称,所以取一半
return axisFreq, result
if __name__ == '__main__':
Fs = 10000 # 采样频率
f1 = 390 # 信号频率1
f2 = 2000 # 信号频率2
t = np.linspace(0, 1, Fs) # 生成 1s 的时间序列
# 给定信号
y = 2 * np.sin(2 * np.pi * f1 * t) + 5 * np.sin(2 * np.pi * f2 * t)
# 第一步,对没有添加噪声的信号进行FFT,验证分析是否正确
x, result = FFT(Fs, y)
# 绘图
fig1 = plt.figure(figsize=(16, 9))
plt.title('original data')
plt.plot(t, y)
plt.xlabel('time/s')
plt.ylabel('Amplitude')
plt.grid()
fig2 = plt.figure(figsize=(16, 9))
plt.title('FFT')
plt.plot(x, result)
plt.xlabel('Frequency/Hz')
plt.ylabel('Amplitude')
plt.grid()
plt.show()输出结果如下:

结果分析:从FFT的结果我们可以看到,在频率为390到2000Hz的地方有两个凸起的“高峰”,说明原信号在此处的频率占据比重较大,而且FFT的结果也满足原信号的幅值大小,即390Hz信号的幅度为2,2000Hz的信号幅度为5。
如果我们对信号进行加噪,可以查看FFT分析结果。
噪声信号选择随机信号,注意,点数要和被分析的信号的点数保持一致。
# 0-1 之间的随机噪声乘以10倍,也即0-10之间的噪声
noise1 = 10*np.random.random(10000)


从图中可以看到的是,加入的噪声信号有直流成分(0Hz),其他横坐标上密密麻麻分布的是一些零碎的频率信号。
参考文章:文章来源:https://www.toymoban.com/news/detail-798175.html
Python 中 FFT 快速傅里叶分析 - 知乎文章来源地址https://www.toymoban.com/news/detail-798175.html
到了这里,关于Python中利用FFT(快速傅里叶变换)进行频谱分析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!