⛄一、边缘计算架构下最优异构路径规划模型
我们考虑一个已经布设好的移动边缘计算场景,在该场景下已部署了一系列的无线接入点、移动边缘云(微云)以及无线充电桩。用A=邀a0,a1,…,am妖表示无线接入点集合,S=邀s0,s1,…,sn妖表示微云集合,B=邀b0,b1,…,bl妖表示无线充电桩集合。考虑实际应用场景为城市,可假设无线接入点已完全覆盖需侦测的场所。同时为节约成本,所有的微云及充电桩都将被部署在无线接入点所在处。因此,可用集合A表示无线接入点、微云、无线充电桩集合。当S(j)=1时,则无线接入点aj处也同时部署了微云;否则S(j)=0。而B(j)则用来表示无线接入点aj与无线充电桩的共存情况。
在该环境下,一组异构移动设备从地、空分别布防,实时无缝的监控地面的情况。用集合D=邀d0,d1,…,dk妖表示k个移动侦测设备。考虑各类设备在移动速度、最大电量等方面各不相同,用θimax和pimax分别表示移动设备di所能达到的最高移动速度和最大可用电量。同时,我们将移动侦测设备可停留的位置离散化,并给每个位置编号邀0,1,…,J妖,并考虑移动设备的两种状态:侦测、传输。设t时刻,设备di所在位置为L(i,t)=邀0,1,…,J妖,状态为R(i,t)=邀1,0妖分别对应传输和侦测状态。则每个移动侦测设备的移动能耗可抽象为:
函数D(A,B)计算A、B两点间的距离,αi为移动政策设备i移动单位距离的平均能耗。城市场景下k个移动侦测设备在T时刻内的总移动能耗可抽象为:
这些移动设备将按照固定的路线移动,相互协调配合完成整个城市范围内的侦测覆盖。这里我们定义侦测覆盖包括时域和空间上的覆盖要求,即每个侦测点在一定时间τ内至少被一个侦测设备访问一次。用二元变量x(i,t,j)表示侦测设备di在t时刻是否能覆盖侦测区域j∈邀0,1,…,J妖。则侦测区域的覆盖性要求可表达为:
同时为了保证服务的低延时,T时刻内数据至少要上传至微云一次,即:
此外,每台移动设备的可用电量受到上下限约束,其任意时刻可用电量大于零:
其中,Pt(i)为移动设备di在t时刻的初始能量,其最大不超过di电池的最大容量pimax:
同时,该移动设备的移动速度不会超过其所能达到的最高移动速度:
将移动边缘场景下移动异构终端的路径规划问题抽象化,以最小化系统总移动能耗(式(2))为目标,兼顾安防场景的覆盖性需求(式(3))、服务的延时需求(式(4))、移动设备的电量约束(式(5)、(6))、速度约束(式(7)),可建立安防场景下最优侦测路径规划问题。
然而,可证明旅行商问题可规约为最优异构路径规划的特殊情况,因此最优异构路径规划也为NP难问题。
⛄二、部分源代码
clc;clear;close all;
tic;
global N; %divide [0,1][0,1] map into NN grid
global N2; % divide [0,1][0,1] map into N2N2 grid when calculating weight matrix
global EPISOD_SUM;
global n; % parameter in sigmoid demand function
global B; % parameter in sigmoid demand function
global OBSER_RADIS; % observe radius 0<x<1
global SERVICE_RADIS; % the radius within which a TU can be served
global stepWay; % UAV one step length
global TU_info; % TUs location matrix
global TU_demand_matrix; % TUs service demand weight matrix
global K; %risk coefficient
global M; %service demand coefficient
global imgnum;
global plotFigure;
%% Customized parameters
K=20;
M=1;
isSigmoid=1; % 1-sigmoid,0-linear
plotFigure=1; % 1-Plotting,0-No plotting
%% map information
N=20;
N2=50;
EPISOD_SUM=20*N;
n=2;
B=8;
%% UAV information
OBSER_RADIS=0.2;
SERVICE_RADIS=0.2;
stepWay=0.02;
%% RUN
fprintf(‘K = %.1f, M = %.3f \n’,K,M);
TU_info=getTU_info;
if(isSigmoid==1)
fprintf(‘Using sigmoid demand function.\n’);
TU_demand_matrix=TU_demand;
else
fprintf(‘Using linear demand function.\n’)
TU_demand_matrix=TU_demand_linear;
end
COUNT=zeros(1,size(TU_info,1)); % count each TU service time
initialize;
drawBackground;
main_UAVs;
%% Print results
[PL,ServiceRate,Risk]=measure;
toc;
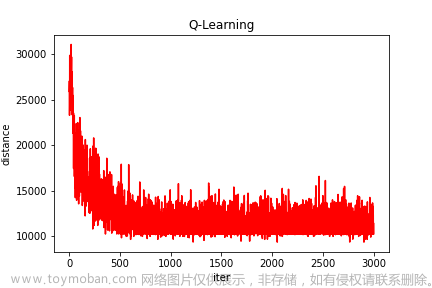
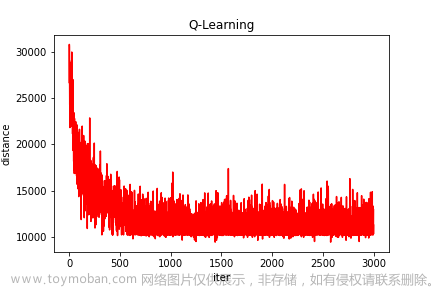
⛄三、运行结果

⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]强士卿,孙滢.城市安防场景下基于边缘计算的三维侦测路径规划[J].工业控制计算机. 2019,32(12)文章来源:https://www.toymoban.com/news/detail-798236.html
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除文章来源地址https://www.toymoban.com/news/detail-798236.html
到了这里,关于【无人机】强化学习的多无人机移动边缘计算与路径规划【含Matlab源码 2426期】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!