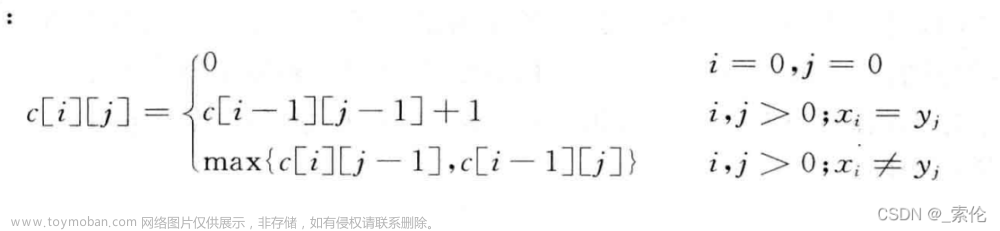【算法】力扣【动态规划，LCS】1143. 最长公共子序列-Toy模板网

这篇具有很好参考价值的文章主要介绍了【算法】力扣【动态规划，LCS】1143. 最长公共子序列。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1143. 最长公共子序列

【算法】力扣【动态规划，LCS】1143. 最长公共子序列

题目描述

本文是对LCS这一动态规划模型的整理，以力扣平台上的算法题1143：最长公共子序列为模板题进行解析。

该题目要求计算两个字符串的最长公共子序列（Longest Common Subsequence，简称LCS）的长度。字符串的子序列是指在不改变字符顺序的情况下，通过删去某些字符后形成的新字符串。如果两个字符串没有公共子序列，返回0。

输入输出示例

示例 1:

输入：text1 = “abcde”, text2 = “ace”
输出：3
解释： 最长公共子序列是 “ace” ，其长度为3。

示例 2:

输入：text1 = “abc”, text2 = “abc”
输出：3
解释： 最长公共子序列是 “abc” ，其长度为3。

示例 3:

输入：text1 = “abc”, text2 = “def”
输出：0
解释： 两个字符串没有公共子序列，返回0。

提示

1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成。

解题思路

为了解决该问题，我们使用动态规划的方法。定义状态dp(i, j)来表示text1[0...i-1]和text2[0...j-1]这两个字符串的LCS长度。dp(len1, len2)将会是我们要求解的答案，其中len1和len2分别是text1和text2的长度。

状态转移方程

如果text1[i - 1] == text2[j - 1]，那么dp(i, j) = dp(i - 1, j - 1) + 1。
否则，dp(i, j) = max(dp(i - 1, j), dp(i, j - 1))。

边界条件

当i == 0或j == 0时，即其中一个字符串长度为0，dp(i, j)必然为0。

代码解析

下面是使用C++实现的解决方案：

class Solution {
public:
    vector<vector<int>> memo;
    vector<vector<bool>> vis;
    string text1;
    string text2;
    
    int longestCommonSubsequence(string text1, string text2) {
        int len1 = text1.size(), len2 = text2.size();
        this->text1 = text1;
        this->text2 = text2;

        // 初始化记忆化数组
        memo = vector<vector<int>>(len1 + 1, vector<int>(len2 + 1, 0));
        vis = vector<vector<bool>>(len1 + 1, vector<bool>(len2 + 1, 0));
        
        // 从最大问题规模开始求解
        return dp(len1, len2);
    }

    // 主要的递归函数，用于解决子问题
    inline int dp(int i, int j) {
        // 边界条件处理
        if (i <= 0 || j <= 0) return 0;

        // 通过vis数组判断当前子问题是否已经解决过
        if (vis[i][j]) return memo[i][j];
        
        // 递归计算子问题
        int sub_solve_0 = dp(i - 1, j - 1);
        int sub_solve_1 = dp(i - 1, j);
        int sub_solve_2 = dp(i, j - 1);

        // 转移方程逻辑处理
        // 这里 i - 1 和 j - 1是因为i和j代表长度，
        // 减一后才是真实索引值。
        if (text1[i - 1] == text2[j - 1]) {
            memo[i][j] = sub_solve_0 + 1;
        } else {
            memo[i][j] = max(sub_solve_1, sub_solve_2);
        }
        
        // 标记当前子问题已解决并返回结果
        vis[i][j] = true;
        return memo[i][j];
    }
};

复杂度分析

时间复杂度： $\times m)$ ，其中 $n$ 和 $m$ 分别是text1和text2的长度。每对索引组合(i, j)最多只会被计算一次。
空间复杂度： $\times m)$ ，用于存储所有子问题的解。

结论

动态规划提供了一种有效的方法，该方法通过分解为更小的子问题，并存储这些子问题的解来避免重复计算。这是动态规划的核心。使用动态规划求解LCS问题，我们通常使用选或不选子序列中的某一元素的思路来推导最长公共子序列中的元素组成，可以通过将两个串各自的长度作为问题规模看待，自顶向下地不断减小问题规模，再自底向上地利用子问题的解得到原问题的解。

注：LCS问题通常涉及2或者更多个串，但有时候也只会涉及一个串（比如1312. 让字符串成为回文串的最少插入次数），一般来说，对于这些串中的元素，从某种形式上可以按顺序（子序列是有顺序的）进行相互匹配（满足某种关系，比如相等…）。文章来源地址https://www.toymoban.com/news/detail-798509.html

到了这里，关于【算法】力扣【动态规划，LCS】1143. 最长公共子序列的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！