1. Toy模板网首页
  2. > Toy博客

探索Python数据结构与算法：解锁编程的无限可能

10月前 作者：忆~遂愿 分类：Toy博客 阅读(48) 违法举报

这篇具有很好参考价值的文章主要介绍了探索Python数据结构与算法：解锁编程的无限可能。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

探索Python数据结构与算法：解锁编程的无限可能,Python编程的脉动之声,算法探索,python,数据结构,算法,动态规划,人工智能,边缘计算,图像处理

重温Python，适合新手搭建知识体系，也适合大佬的温故知新~

由于涉及到算法，知识深度非常深，本文只讲表层来重温记忆，想要深入需要自行多加了解和刷题哈

一、引言

1.1 数据结构与算法对于编程的重要性

重要性：

  1. 提高程序效率：优秀的数据结构和算法可以显著提高程序的执行效率。数据结构和算法的选择会直接影响到程序的运行时间和空间复杂度。合理地选择和设计数据结构和算法，可以降低程序的时间和空间开销，从而提高程序的性能。
  2. 解决复杂问题：数据结构和算法是解决复杂问题的基础。通过选择合适的数据结构和算法，可以将复杂的问题分解为更小的子问题，并通过适当的算法解决这些子问题。通过组合使用不同的数据结构和算法，可以有效地解决各种复杂的计算问题。
  3. 提升代码质量和可维护性：良好的数据结构和算法设计可以提高代码的质量和可维护性。合适的数据结构可以使代码更加清晰、简洁，并且易于理解和维护。同时，合理的算法设计可以使代码更加可读性高，减少错误和bug的产生。
  4. 培养编程思维：学习数据结构和算法可以培养良好的编程思维。对于解决问题和优化程序有一定的抽象思考能力、分析和设计能力等都是非常重要的。通过学习数据结构和算法，可以培养这些编程思维，提高解决问题的能力。
  5. 面试和竞争：在面试和竞争中，数据结构和算法是被广泛考察的内容。很多技术公司在面试过程中会对候选人的数据结构和算法知识进行考察，因为它们认为这是评估候选人编程能力和解决问题能力的重要指标。

综上所述，数据结构和算法对于编程非常重要。它们能够提高程序效率、解决复杂问题、改善代码质量和可维护性，培养编程思维，并在面试和竞争中起到重要作用。因此，掌握数据结构和算法是每个程序员都应该具备的基本技能。

1.2 Python作为实现数据结构与算法的强大工具

Python作为一种高级编程语言，提供了丰富的库和功能，使其成为实现数据结构和算法的强大工具。

Python在这方面的一些优势：

  1. 内置数据结构：Python提供了许多内置的数据结构，如列表、元组、字典和集合等。这些数据结构的使用非常简单和灵活，可以满足大部分基本的数据存储和操作需求。
  2. 强大的标准库：Python的标准库提供了许多有用的模块和函数，支持各种常用的数据结构和算法。例如，collections模块提供了更高级的数据结构，如有序字典、命名元组和堆队列等；heapq模块提供了堆排序相关的函数；itertools模块提供了迭代器和组合函数等。
  3. 第三方库的丰富性：Python生态系统中存在许多强大的第三方库，如NumPy、Pandas和SciPy等，它们提供了高效的数据处理和科学计算能力。此外，还有专门用于机器学习和深度学习的库，如TensorFlow和PyTorch。这些库使得在Python中实现复杂的数据结构和算法变得更加容易和高效。
  4. 简洁易读的语法：Python的语法非常简洁易读，特别适合表达和实现复杂的数据结构和算法。它具有清晰的代码组织风格，使得代码更易于理解、调试和维护。
  5. 大量的学习资源：Python作为一门广泛使用的编程语言，拥有大量的学习资源和社区支持。有许多优秀的书籍、课程和在线教程，以及活跃的开发者社区，可以帮助初学者快速上手和深入学习数据结构和算法。

总的来说，Python作为实现数据结构和算法的工具具有许多优势，使得Python成为一个受欢迎的选择，无论是在学术研究、工业应用还是个人项目中，都能轻松地实现各种复杂的数据结构和算法。

二、列表和元组

2.1 列表：创建列表、索引、切片和常用操作

列表是一种有序、可变的数据结构。它可以存储多个元素，并且支持索引、切片和常用操作。

  1. 创建列表：

    my_list = []  # 创建一个空列表
my_list = [1, 2, 3]  # 创建一个包含三个整数的列表
my_list = ['apple', 'banana', 'orange']  # 创建一个包含三个字符串的列表

  2. 索引： 列表中的元素通过索引来访问，索引从0开始，负数索引表示从列表末尾开始倒数。

    my_list = ['apple', 'banana', 'orange']
print(my_list[0])  # 输出：'apple'
print(my_list[-1])  # 输出：'orange'

  3. 切片： 可以使用切片操作获取列表的子集。

    my_list = ['apple', 'banana', 'orange', 'grape', 'melon']
print(my_list[1:3])  # 输出：['banana', 'orange']
print(my_list[:2])  # 输出：['apple', 'banana']
print(my_list[2:])  # 输出：['orange', 'grape', 'melon']

  4. 修改列表元素： 列表的元素是可变的，可以通过索引来修改它们。

    my_list = ['apple', 'banana', 'orange']
my_list[1] = 'kiwi'
print(my_list)  # 输出：['apple', 'kiwi', 'orange']

  5. 添加元素： 可以使用append()方法在列表末尾添加一个元素，或使用insert()方法在指定位置插入一个元素。

    my_list = ['apple', 'banana', 'orange']
my_list.append('grape')
print(my_list)  # 输出：['apple', 'banana', 'orange', 'grape']

my_list.insert(1, 'kiwi')
print(my_list)  # 输出：['apple', 'kiwi', 'banana', 'orange', 'grape']

  6. 删除元素： 可以使用del语句按索引删除元素，或使用remove()方法根据元素的值删除元素。

    my_list = ['apple', 'banana', 'orange']
del my_list[1]
print(my_list)  # 输出：['apple', 'orange']

my_list.remove('orange')
print(my_list)  # 输出：['apple']

  7. 其他常用操作：

    • 使用len()函数获取列表的长度。
    • 使用in关键字检查元素是否存在于列表中。
    • 使用+运算符拼接多个列表。
    • 使用*运算符重复列表。
    • 使用max()和min()函数获取列表中的最大值和最小值。

以上只是列表的一些基本操作和常见用法，Python的列表还有很多其他的功能和方法，读者可自行查找资料，深入学习。

2.2 元组：不可变序列的特性和使用场景

元组是一种不可变的有序序列。与列表不同，元组的元素不能被修改、添加或删除。以下是元组的一些特性和使用场景：

  1. 不可变性： 元组是不可变的，一旦创建后，其元素不能被修改。这意味着你无法对元组进行赋值操作，也无法通过索引来修改元素。这个特性使得元组具有更高的安全性和稳定性，适用于存储不希望被改变的数据。
  2. 数据保护： 元组的不可变性可以保护其中的数据不被意外修改。这对于存储一些重要的配置信息、常量或敏感数据等很有用。如果你希望某个数据在程序运行过程中不被修改，可以将其放入元组中。
  3. 作为字典的键： 元组可以作为字典的键，而列表不能。因为字典的键必须是不可变的，而元组的不可变性使得它成为字典中的有效键。这样可以方便地创建包含键值对的数据结构。
  4. 函数返回值： 元组经常用作函数的返回值，特别是当函数需要返回多个值时。通过返回一个元组，可以方便地将多个值打包起来，并且接收函数返回值的时候可以使用元组的解包操作。
  5. 解包和迭代： 元组支持解包操作，可以将元组中的元素分别赋值给多个变量。这种方式在函数返回多个值时非常方便。同时，可以使用for循环来遍历元组的元素，或者使用内置的enumerate()函数同时获取索引和对应的元素。

演示使用元组场景：

# 元组的创建
my_tuple = (1, 2, 3)
print(my_tuple)  # 输出：(1, 2, 3)

# 元组的索引
print(my_tuple[0])  # 输出：1

# 元组的解包
x, y, z = my_tuple
print(x, y, z)  # 输出：1 2 3

# 元组作为字典的键
my_dict = {(1, 2): 'hello', (3, 4): 'world'}
print(my_dict[(1, 2)])  # 输出：'hello'

# 函数返回值为元组
def square_and_cube(x):
    return x ** 2, x ** 3

result = square_and_cube(2)
print(result)  # 输出：(4, 8)

ps：如果元组只有一个元素，需要在元素后面加上逗号，以确保它被正确地识别为元组：(1,) 。

三、字符串操作和正则表达式

3.1 字符串的常见操作和方法

1.访问字符： 字符串中的每个字符都有一个对应的索引，可以使用索引操作来访问单个字符。

my_str = "Hello"
print(my_str[0])  # 输出：H

2.切片操作： 可以使用切片操作从字符串中提取子字符串。

my_str = "Hello World"
print(my_str[1:5])  # 输出：ello

3.连接字符串： 使用加号（+）运算符来连接两个字符串。

str1 = "Hello"
str2 = "World"
print(str1 + " " + str2)  # 输出：Hello World

4.查询子字符串： 使用in关键字来查询一个子字符串是否在一个字符串中。

my_str = "Hello World"
print("lo" in my_str)  # 输出：True

5.分割字符串： split()方法可以用于将一个字符串按照指定分隔符分割成多个子字符串，并返回一个列表。

my_str = "Hello,World,How,Are,You"
split_str = my_str.split(",")
print(split_str)  # 输出：['Hello', 'World', 'How', 'Are', 'You']

6.连接字符串： join()方法可以用于将一个列表中的多个子字符串连接成一个字符串。

split_str = ['Hello', 'World', 'How', 'Are', 'You']
join_str = ",".join(split_str)
print(join_str)  # 输出：Hello,World,How,Are,You

7.大小写转换和去除空格： upper()方法可以将字符串中的所有字母转换为大写形式，lower()方法可以将其转换为小写形式。strip()方法可以去除字符串两端的空格。

my_str = "   Hello World   "
print(my_str.upper())  # 输出：   HELLO WORLD   
print(my_str.lower())  # 输出：   hello world   
print(my_str.strip())  # 输出：Hello World

这些示例涵盖了Python中字符串常见操作和方法的一部分，这里只是提供了一些基本的示例，实际上还有许多其他有用的函数和方法可供使用。

3.2 正则表达式的基本语法和应用

正则表达式（Regular Expression）是一种强大的文本匹配工具，用于在字符串中查找和匹配特定的模式。在Python中，通过re模块可以使用正则表达式。

正则表达式的基本语法和应用的示例和代码演示：

1.导入re模块： 在使用正则表达式之前，需要先导入Python的re模块。

import re

2.匹配字符串开头或结尾： 可以使用^符号匹配行的开头，使用$符号匹配行的结尾。

pattern = r"^Hello"
text = "Hello World"
match = re.search(pattern, text)
if match:
    print("Match found!")
else:
    print("Match not found.")
    
# 输出结果
Match found!

3.匹配任意字符： 使用.匹配任意字符（除了换行符）。

pattern = r"he..o"
text = "hello"
match = re.search(pattern, text)
if match:
    print("Match found!")
else:
    print("Match not found.")
    
# 输出结果
Match found!

4.匹配多个字符： 使用[]来匹配其中的任意一个字符。

pattern = r"[aeiou]"
text = "hello"
match = re.search(pattern, text)
if match:
    print("Match found!")
else:
    print("Match not found.")
        
# 输出结果
Match found!

5.匹配重复字符： 使用*匹配零个或多个重复字符。

pattern = r"a*"
text = "aabbb"
match = re.search(pattern, text)
if match:
    print("Match found!")
else:
    print("Match not found.")
        
# 输出结果
Match found!

6.使用特殊字符： 正则表达式中有一些特殊字符具有特殊的含义，如\d用于匹配数字字符，\w用于匹配字母、数字和下划线等。

pattern = r"\d+"
text = "12345"
match = re.search(pattern, text)
if match:
    print("Match found!")
else:
    print("Match not found.")
        
# 输出结果
Match found!

7.分组和提取： 可以使用小括号来创建一个组，并通过group()方法提取匹配到的内容。

pattern = r"(hello) (world)"
text = "hello world"
match = re.search(pattern, text)
if match:
    print(match.group(0))  # 输出：hello world
    print(match.group(1))  # 输出：hello
    print(match.group(2))  # 输出：world

ps：使用正则表达式时，可以在模式字符串前加上r前缀，表示原始字符串，避免转义字符的问题。

四、字典和集合

4.1 字典：键-值对的集合和常见操作

Python中的字典（Dictionary）是一种用于存储键-值对的数据结构，可以使用键来访问和操作相应的值。

字典的基本操作和示例代码：

1.创建一个字典： 可以使用花括号将键-值对列表括起来，或使用dict()函数来创建一个空字典。

# 使用花括号创建字典
my_dict = {"apple": 1, "banana": 2, "orange": 3}
# 使用dict()函数创建字典
my_dict2 = dict()

2.访问字典中的值： 可以使用键来访问相应的值。

my_dict = {"apple": 1, "banana": 2, "orange": 3}
print(my_dict["apple"])  # 输出：1

3.添加或修改字典中的元素： 可以使用键来添加新的键-值对或修改已有的键-值对。

my_dict = {"apple": 1, "banana": 2, "orange": 3}
# 添加新的键-值对
my_dict["peach"] = 4
# 修改已有的键-值对
my_dict["banana"] = 5

4.删除字典中的元素： 可以使用del关键字来删除指定键的键-值对。

my_dict = {"apple": 1, "banana": 2, "orange": 3}
del my_dict["apple"]

5.字典遍历： 可以使用for循环来遍历字典中的所有键-值对。

my_dict = {"apple": 1, "banana": 2, "orange": 3}
for key, value in my_dict.items():
    print(key, value)

6.检查字典中是否包含指定的键或值： 可以使用in关键字来检查字典中是否包含指定的键或值。

my_dict = {"apple": 1, "banana": 2, "orange": 3}
# 检查是否包含指定的键
if "apple" in my_dict:
    print("Apple found!")
# 检查是否包含指定的值
if 1 in my_dict.values():
    print("Value found!")

ps：键必须是不可变的类型（如字符串、数字或元组等），因为它们被用作字典中的索引。

4.2 集合：无序不重复元素的集合和常见操作

在Python中，集合（Set）是一种无序且不重复的数据结构，用于存储唯一的元素。

集合的基本操作和示例代码：

1.创建一个集合： 可以使用花括号将元素列表括起来，或使用set()函数来创建一个空集合。

# 使用花括号创建集合
my_set = {1, 2, 3}
# 使用set()函数创建集合
my_set2 = set()

2.添加元素到集合中： 可以使用add()方法向集合中添加单个元素，或使用update()方法添加多个元素。

my_set = {1, 2, 3}
my_set.add(4)
my_set.update([5, 6])

3.删除集合中的元素： 可以使用remove()方法删除指定的元素，如果元素不存在则会引发KeyError错误；或使用discard()方法删除指定的元素，如果元素不存在则不会引发错误。

my_set = {1, 2, 3}
my_set.remove(2)
my_set.discard(4)

4.集合运算： 可以使用集合运算符进行交集、并集、差集和对称差集等操作。

set1 = {1, 2, 3}
set2 = {3, 4, 5}

# 交集
intersection = set1 & set2

# 并集
union = set1 | set2

# 差集
difference = set1 - set2

# 对称差集
symmetric_difference = set1 ^ set2

5.集合遍历： 可以使用for循环遍历集合中的所有元素。

my_set = {1, 2, 3}
for item in my_set:
    print(item)

6.检查集合中是否包含指定的元素： 可以使用in关键字来检查集合中是否包含指定的元素。

my_set = {1, 2, 3}
if 1 in my_set:
    print("Element found!")

ps：集合中的元素必须是不可变的类型（如数字、字符串或元组等），不能包含可变的类型（如列表或字典）。

五、栈和队列

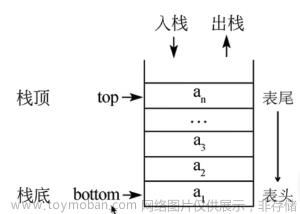
5.1 栈：后进先出的数据结构和应用场景

栈是一种后进先出（LIFO，Last In First Out）的数据结构，类似于我们平时叠放的一堆盘子，只能从最顶层取出盘子。在Python中，可以使用列表（List）来实现栈的功能。

简单的栈示例代码：

class Stack:
    def __init__(self):
        self.stack = []

    # 判断栈是否为空，返回布尔值
    def is_empty(self):
        return len(self.stack) == 0

    # 将元素item压入栈顶
    def push(self, item):
        self.stack.append(item)

    # 弹出栈顶元素，并返回该元素
    def pop(self):
        if self.is_empty():
            return None
        return self.stack.pop()

    # 返回栈顶元素，但不弹出
    def peek(self):
        if self.is_empty():
            return None
        return self.stack[-1]

    # 返回栈中元素的个数
    def size(self):
        return len(self.stack)

如何使用栈来判断字符串中的括号是否匹配：

# 遍历了输入的字符串，如果遇到左括号，则将其压入栈中；如果遇到右括号，则从栈顶弹出一个元素。最后，我们只需判断栈是否为空，即可确定括号是否匹配。
def check_brackets(string):
    stack = Stack()

    for char in string:
        if char == '(':
            stack.push(char)
        elif char == ')':
            if stack.is_empty():
                return False
            stack.pop()

    return stack.is_empty()

# 测试
print(check_brackets("((()))"))  # True
print(check_brackets("()()()"))  # True
print(check_brackets("()(()))")   # False

栈还可以用于其他场景，如函数调用栈、表达式求值等。

5.2 队列：先进先出的数据结构和应用场景

队列是一种先进先出（FIFO，First In First Out）的数据结构，类似于我们平时排队等候的场景，先来的人先被服务。在Python中，可以使用列表（List）或者双端队列（deque）来实现队列的功能。

使用列表实现队列：

class Queue:
    def __init__(self):
        self.queue = []

    def is_empty(self):
        return len(self.queue) == 0

    def enqueue(self, item):
        self.queue.append(item)

    def dequeue(self):
        if self.is_empty():
            return None
        return self.queue.pop(0)

    def size(self):
        return len(self.queue)

使用双端队列（deque）实现队列：

from collections import deque

class Queue:
    def __init__(self):
        self.queue = deque()

    # 判断队列是否为空，返回布尔值
    def is_empty(self):
        return len(self.queue) == 0

    # 将元素item加入队列尾部
    def enqueue(self, item):
        self.queue.append(item)

    # 移除并返回队列的第一个元素
    def dequeue(self):
        if self.is_empty():
            return None
        return self.queue.popleft()

    # 返回队列中元素的个数
    def size(self):
        return len(self.queue)

使用队列实现打印任务调度：

# 将需要打印的任务加入到队列中，然后从队列中取出任务交给打印机进行打印，实现了一个简单的打印任务调度。
# 打印队列类（PrintQueue）
class PrintQueue:
    def __init__(self):
        self.queue = Queue()

    def enqueue(self, task):
        self.queue.enqueue(task)

    def dequeue(self):
        return self.queue.dequeue()

    def is_empty(self):
        return self.queue.is_empty()

    def size(self):
        return self.queue.size()

# 打印机类（Printer）
class Printer:
    def __init__(self):
        self.current_task = None

    def get_task(self, task):
        self.current_task = task

    def print_task(self):
        if self.current_task is not None:
            print("正在打印任务：", self.current_task)
            self.current_task = None
        else:
            print("没有任务需要打印")


def simulate_printing(tasks):
    printer = Printer()
    print_queue = PrintQueue()

    for task in tasks:
        print_queue.enqueue(task)

    while not print_queue.is_empty():
        next_task = print_queue.dequeue()
        printer.get_task(next_task)
        printer.print_task()

    print("打印完成！")


# 测试
tasks = ["任务1", "任务2", "任务3", "任务4"]
simulate_printing(tasks)

队列还可以用于其他场景，如消息传递、多线程编程等。

六、链表

6.1 单向链表和双向链表的实现和操作

链表是一种常见的数据结构，主要用于存储一系列元素，每个元素都包含一个指向下一个元素的指针。链表可以分为单向链表和双向链表两种类型。

  • 单向链表中，每个节点包含一个值和一个指向下一个节点的引用；
  • 双向链表中，每个节点不仅包含一个值，还包含一个指向前一个节点的引用。

单向链表的实现：

class Node:
    def __init__(self, data):
        self.data = data
        self.next_node = None

class LinkedList:
    def __init__(self):
        self.head = None

    def is_empty(self):
        return self.head is None

    def add(self, data):
        new_node = Node(data)
        new_node.next_node = self.head
        self.head = new_node

    def size(self):
        count = 0
        current_node = self.head
        while current_node is not None:
            count += 1
            current_node = current_node.next_node
        return count

    def search(self, data):
        current_node = self.head
        while current_node is not None:
            if current_node.data == data:
                return True
            current_node = current_node.next_node
        return False

    def delete(self, data):
        previous_node = None
        current_node = self.head
        while current_node is not None:
            if current_node.data == data:
                if previous_node is None:
                    self.head = current_node.next_node
                else:
                    previous_node.next_node = current_node.next_node
                return
            previous_node = current_node
            current_node = current_node.next_node

双向链表的实现：

class Node:
    def __init__(self, data):
        self.data = data
        self.previous_node = None
        self.next_node = None

class LinkedList:
    def __init__(self):
        self.head = None
        self.tail = None

    def is_empty(self):
        return self.head is None

    def add(self, data):
        new_node = Node(data)
        if self.is_empty():
            self.head = new_node
            self.tail = new_node
        else:
            new_node.previous_node = self.tail
            self.tail.next_node = new_node
            self.tail = new_node

    def size(self):
        count = 0
        current_node = self.head
        while current_node is not None:
            count += 1
            current_node = current_node.next_node
        return count

    def search(self, data):
        current_node = self.head
        while current_node is not None:
            if current_node.data == data:
                return True
            current_node = current_node.next_node
        return False

    def delete(self, data):
        current_node = self.head
        while current_node is not None:
            if current_node.data == data:
                if current_node.previous_node is None:
                    self.head = current_node.next_node
                else:
                    current_node.previous_node.next_node = current_node.next_node
                if current_node.next_node is None:
                    self.tail = current_node.previous_node
                else:
                    current_node.next_node.previous_node = current_node.previous_node
                return
            current_node = current_node.next_node

使用链表实现一个队列：

class Node:
    def __init__(self, data):
        self.data = data
        self.next_node = None

class Queue:
    def __init__(self):
        self.head = None
        self.tail = None

    def is_empty(self):
        return self.head is None

    def enqueue(self, data):
        new_node = Node(data)
        if self.is_empty():
            self.head = new_node
            self.tail = new_node
        else:
            self.tail.next_node = new_node
            self.tail = new_node

    def dequeue(self):
        if self.is_empty():
            return None
        else:
            data = self.head.data
            self.head = self.head.next_node
            return data

    def size(self):
        count = 0
        current_node = self.head
        while current_node is not None:
            count += 1
            current_node = current_node.next_node
        return count

6.2 链表的优势和应用

优势和应用：

  1. 动态性：链表的长度可以根据需要动态变化，不像数组一样需要提前指定大小。这使得链表在需要频繁插入和删除元素的场景下非常高效。
  2. 内存灵活使用：链表以节点的形式存储元素，每个节点都包含一个指向下一个节点的引用。这种存储方式使得链表可以更灵活地利用内存空间，不需要一段连续的内存空间。
  3. 插入和删除操作高效：由于链表的动态性和内存灵活使用的特点，插入和删除元素的操作非常高效。
    1. 对于单向链表，插入和删除操作只需要修改节点的引用，时间复杂度为O(1)；
    2. 对于双向链表，还可以通过修改前后节点的引用来实现插入和删除操作，同样时间复杂度为O(1)。
  4. 高效的迭代：链表可以通过节点引用顺序访问元素，因此可以很方便地进行迭代操作。与数组不同，链表不需要考虑扩容和缩容的问题，所以在大规模数据处理和遍历操作上更加高效。
  5. 应用场景：链表在许多场景中都有广泛的应用。
    1. 例如，LRU缓存算法中可以使用链表来实现缓存的淘汰策略；
    2. 在图的表示中，可以使用链表来表示图的邻接表；
    3. 在实现栈、队列等数据结构时，链表也是常用的基础数据结构。

总之，链表作为一种常见的数据结构，在Python中具有动态性、内存灵活使用、插入删除操作高效和高效迭代等优势，并广泛应用于各种场景中。

七、树和图

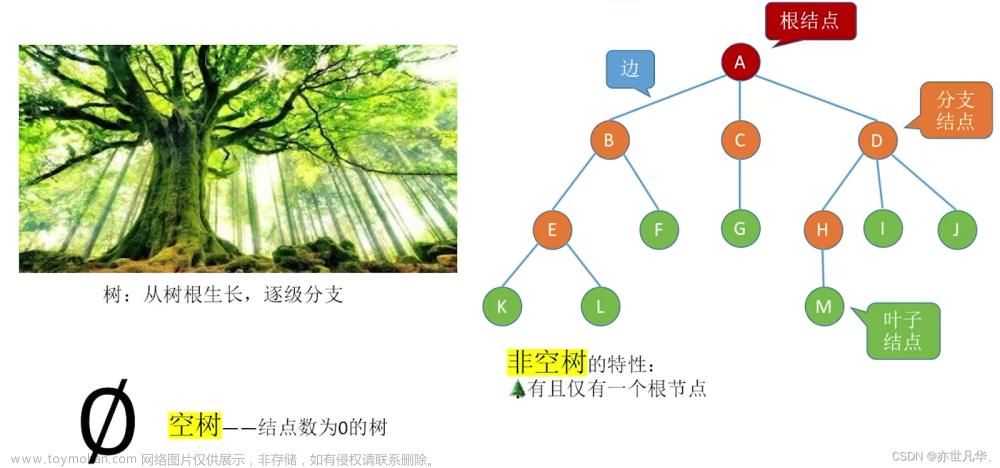
7.1 树的基本概念和遍历方法

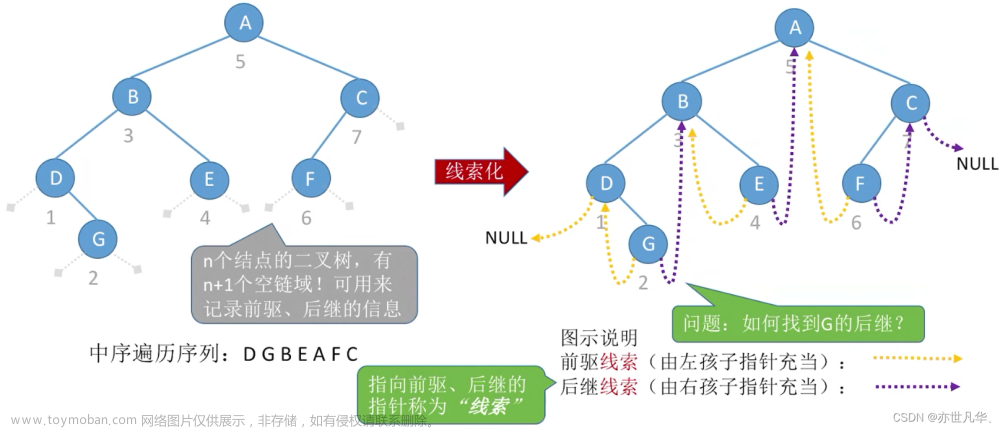
在Python中，树是一种非常常见的数据结构，它由节点组成，每个节点有零个或多个子节点。树的遍历是指按照一定顺序访问树中的所有节点，包括根节点和叶子节点。常用的树的遍历方式有三种：前序遍历、中序遍历和后序遍历。

  • 前序遍历：先访问根节点，然后递归地遍历左子树和右子树。
  • 中序遍历：先递归地遍历左子树，然后访问根节点，最后递归地遍历右子树。
  • 后序遍历：先递归地遍历左子树和右子树，最后访问根节点。

创建树并实现前序遍历和中序遍历：

# 树的节点
class Node:
    def __init__(self, data):
        self.data = data
        self.left_child = None
        self.right_child = None

# 创建一颗树
def build_tree():
    root = Node(1)
    root.left_child = Node(2)
    root.right_child = Node(3)
    root.left_child.left_child = Node(4)
    root.left_child.right_child = Node(5)
    root.right_child.left_child = Node(6)
    root.right_child.right_child = Node(7)
    return root

# 前序遍历
def preorder_traversal(node):
    if node is None:
        return
    print(node.data, end=' ')
    preorder_traversal(node.left_child)
    preorder_traversal(node.right_child)

# 中序遍历 
def inorder_traversal(node):
    if node is None:
        return
    inorder_traversal(node.left_child)
    print(node.data, end=' ')
    inorder_traversal(node.right_child)

if __name__ == '__main__':
    root = build_tree()
    print('前序遍历：', end='')
    preorder_traversal(root)
    print('\n中序遍历：', end='')
    inorder_traversal(root)

7.2 图的基本概念和常见算法

在Python中，图是一种非常重要的数据结构，它由节点和边组成。节点代表图中的实体，边表示节点之间的关系或连接。图的遍历是指按照一定顺序访问图中的所有节点和边，包括起始节点和终止节点。常用的图的遍历方式有两种：深度优先搜索和广度优先搜索。

  • 深度优先搜索（DFS）：从一个起始节点出发，递归地访问它的各个邻居节点，直到所有可达节点都被访问过。
  • 广度优先搜索（BFS）：从一个起始节点出发，按照距离递增的顺序依次访问其周围的节点，直到所有可达节点都被访问过。

创建图并实现深度优先搜索和广度优先搜索：

from queue import Queue

class Graph:
    def __init__(self):
        self.vertices = {}
    
    # 添加节点
    def add_vertex(self, vertex):
        if vertex not in self.vertices:
            self.vertices[vertex] = []
    
    # 添加边
    def add_edge(self, v1, v2):
        self.vertices[v1].append(v2)
        self.vertices[v2].append(v1)

    # 深度优先搜索
    def dfs(self, start, visited=None):
        if visited is None:
            visited = set()
        visited.add(start)
        print(start, end=' ')
        for next_vertex in self.vertices[start]:
            if next_vertex not in visited:
                self.dfs(next_vertex, visited)

    # 广度优先搜索
    def bfs(self, start):
        visited = set()
        q = Queue()
        q.put(start)
        visited.add(start)
        while not q.empty():
            vertex = q.get()
            print(vertex, end=' ')
            for next_vertex in self.vertices[vertex]:
                if next_vertex not in visited:
                    visited.add(next_vertex)
                    q.put(next_vertex)
# 创建了一个图并对其进行深度优先搜索和广度优先搜索
if __name__ == '__main__':
    g = Graph()
    for i in range(6):
        g.add_vertex(i)
    g.add_edge(0, 1)
    g.add_edge(0, 2)
    g.add_edge(1, 2)
    g.add_edge(2, 3)
    g.add_edge(3, 4)
    g.add_edge(3, 5)

    print('深度优先搜索：', end='')
    g.dfs(0)
    print('\n广度优先搜索：', end='')
    g.bfs(0)

八、排序和搜索算法

8.1 常见排序算法：冒泡排序、插入排序、选择排序、快速排序、归并排序

在计算机科学中，排序算法是一种将一组元素按照特定顺序排列的算法。常见的排序算法有冒泡排序、插入排序、选择排序、快速排序和归并排序等。

  1. 冒泡排序

冒泡排序是一种简单的排序算法，其基本思想是多次遍历待排序序列，每次比较相邻的两个元素，如果顺序错误就交换它们。时间复杂度为O(n^2)。

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(n-1-i):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr
  1. 插入排序

插入排序是一种简单直观的排序算法，其基本思想是将待排序序列分为已排序区间和未排序区间，每次从未排序区间选择一个元素插入到已排序区间的合适位置。时间复杂度为O(n^2)。

def insertion_sort(arr):
    n = len(arr)
    for i in range(1, n):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j+1] = arr[j]
            j -= 1
        arr[j+1] = key
    return arr
  1. 选择排序

选择排序是一种简单直观的排序算法，其基本思想是将待排序序列分为已排序区间和未排序区间，每次从未排序区间选择一个最小元素放到已排序区间的末尾。时间复杂度为O(n^2)。

def selection_sort(arr):
    n = len(arr)
    for i in range(n-1):
        min_idx = i
        for j in range(i+1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]
    return arr
  1. 快速排序

快速排序是一种高效的排序算法，其基本思想是通过一次划分将待排序序列分成两个子序列，左边序列中的所有元素都比右边序列中的元素小，然后对两个子序列进行递归排序。时间复杂度为O(nlogn)。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr)//2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)
  1. 归并排序

归并排序是一种高效的排序算法，其基本思想是将待排序序列分成若干个子序列，每个子序列都是有序的，然后再将子序列合并成一个有序的序列。时间复杂度为O(nlogn)。

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)

def merge(left, right):
    i, j = 0, 0
    res = []
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            res.append(left[i])
            i += 1
        else:
            res.append(right[j])
            j += 1
    res += left[i:]
    res += right[j:]
    return res

8.2 常见搜索算法：线性搜索、二分搜索

常见的搜索算法包括线性搜索和二分搜索。

  1. 线性搜索

线性搜索（也称为顺序搜索）是一种简单直观的搜索算法，其基本思想是从待搜索序列的第一个元素开始逐个比较，直到找到目标元素或者遍历完整个序列。时间复杂度为O(n)。

def linear_search(arr, target):
    n = len(arr)
    for i in range(n):
        if arr[i] == target:
            return i
    return -1
  1. 二分搜索

二分搜索（也称为折半搜索）是一种高效的搜索算法，其前提是待搜索序列已经按照升序或降序排列。其基本思想是将待搜索序列分成两个子序列，如果目标元素小于中间元素，则在左侧子序列中继续搜索，否则在右侧子序列中继续搜索，直到找到目标元素或者子序列为空。时间复杂度为O(logn)。

def binary_search(arr, target):
    left, right = 0, len(arr)-1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

九、动态规划和贪心算法

9.1 动态规划的基本思想和应用

动态规划（Dynamic Programming）是一种用于解决具有重叠子问题和最优子结构性质的问题的算法设计方法。其基本思想是将原问题分解为若干个子问题，并先求解子问题的解，然后通过子问题的解推导出原问题的解。动态规划常用于优化问题，可以大大减少重复计算，提高效率。

动态规划的基本步骤：

  1. 定义状态：将原问题划分成若干个子问题，并定义状态表示子问题的解。
  2. 确定状态转移方程：根据子问题之间的关系，得到子问题的状态转移方程。
  3. 确定边界条件：确定最简单的子问题的解，作为边界条件。
  4. 确定计算顺序：根据状态转移方程，确定子问题的计算顺序，通常采用自底向上的方式进行计算。
  5. 计算最终结果：根据计算顺序，计算出原问题的解。

动态规划广泛应用于各个领域，包括但不限于以下几个方面：

  1. 最优化问题：如背包问题、旅行商问题等。
  2. 路径搜索问题：如最短路径问题、最长公共子序列问题等。
  3. 字符串处理问题：如编辑距离问题、正则表达式匹配问题等。
  4. 组合优化问题：如排列组合问题、划分问题等。
  5. 矩阵链乘法问题、最大子数组和问题等。

动态规划算法的关键是找到合适的状态定义和状态转移方程，通过合理地设计问题的划分和求解顺序，可以高效地解决一些复杂的优化问题。

9.2 贪心算法的基本思想和应用

贪心算法（Greedy Algorithm）是一种在每个阶段选择当前最优解的策略，以希望最终能够得到全局最优解的算法。其基本思想是通过局部最优选择来达到全局最优。

贪心算法的基本步骤：

  1. 定义问题的子问题和局部最优解的性质。
  2. 根据局部最优解的性质，构建一个最优解的解空间。
  3. 通过贪心选择原则，逐步构建问题的最优解。
  4. 判断最终解是否是全局最优解。

贪心算法的关键是确定选择的贪心策略，即在每个阶段都选择当前最优的解，以期望最终得到全局最优解。然而，贪心算法并不一定能够得到全局最优解，因为当前最优解未必能够导致全局最优解。因此，在使用贪心算法时需要谨慎选择贪心策略，确保其能够满足问题的要求。

贪心算法广泛应用于各个领域，包括但不限于以下几个方面：

  1. 最小生成树：如Prim算法和Kruskal算法。
  2. 单源最短路径：如Dijkstra算法。
  3. 哈夫曼编码：用于数据压缩。
  4. 区间调度问题：如活动选择问题。
  5. 背包问题的近似算法：如分数背包问题。

贪心算法的优势在于其简单性和高效性。相对于动态规划等算法，贪心算法通常具有较低的时间复杂度，能够在较短的时间内得到一个可接受的解。然而，贪心算法也存在局限性，不能保证一定能够得到全局最优解，因此在使用时需要根据具体问题进行评估和选择。

十、 实践项目 ： 实现一个简单的推荐系统

推荐系统是通过分析用户的历史行为和偏好，给用户提供个性化的推荐内容。

具体步骤：

  • 收集用户信息：收集用户的偏好、历史行为等信息，可以使用表格或数据库存储。
  • 特征提取：根据用户的信息特征，对内容进行特征提取和表示，例如使用关键词、标签等描述内容。
  • 相似度计算：计算不同内容之间的相似度，可以使用余弦相似度等方法。
  • 推荐生成：根据用户的偏好和相似度计算，生成推荐列表并呈现给用户。

简单Demo：

# 定义内容和用户信息
content = {
    'article1': ['Python', '机器学习'],
    'article2': ['Java', '系统开发'],
    'article3': ['Python', '深度学习'],
    'article4': ['C++', '算法'],
    'article5': ['Python', '数据科学']
}

user1 = ['Python', '机器学习']
user2 = ['Java', '系统开发']
user3 = ['Python', '深度学习']

# 计算相似度
def similarity(user, content):
    user_set = set(user)
    content_set = set(content)
    intersection = user_set.intersection(content_set)
    union = user_set.union(content_set)
    return len(intersection) / len(union)

# 生成推荐列表
def generate_recommendations(user, content):
    recommendations = []
    for item in content:
        sim = similarity(user, content[item])
        recommendations.append((item, sim))
    recommendations.sort(key=lambda x: x[1], reverse=True)
    return recommendations

# 获取推荐列表
user = user1
recommendations = generate_recommendations(user, content)

# 打印推荐列表
print("推荐列表：")
for item, sim in recommendations:
    print(f"{item}，相似度：{sim}")

以蝼蚁之行，展鸿鹄之志文章来源地址https://www.toymoban.com/news/detail-798600.html

到了这里，关于探索Python数据结构与算法：解锁编程的无限可能的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 学习高级数据结构：探索平衡树与图的高级算法

    学习高级数据结构：探索平衡树与图的高级算法

    🎉欢迎来到数据结构学习专栏~学习高级数据结构：探索平衡树与图的高级算法 ☆* o(≧▽≦)o *☆嗨~我是IT·陈寒🍹 ✨博客主页：IT·陈寒的博客 🎈该系列文章专栏：数据结构学习 📜其他专栏：Java学习路线 Java面试技巧 Java实战项目 AIGC人工智能 数据结构学习 🍹文章作者技

    2024年02月09日
    浏览(45)
  • 【编程实践】JVM内存管理的核心数据结构和算法思想&代码示例说明

    【编程实践】JVM内存管理的核心数据结构和算法思想&代码示例说明

    2024年02月06日
    浏览(40)
  • 数据结构--》解锁数据结构中树与二叉树的奥秘（一）

    数据结构--》解锁数据结构中树与二叉树的奥秘（一）

            数据结构中的树与二叉树，是在建立非线性数据结构方面极为重要的两个概念。它们不仅能够模拟出生活中各种实际问题的复杂关系，还常被用于实现搜索、排序、查找等算法，甚至成为一些大型软件和系统中的基础设施。         无论你是初学者还是进阶者

    2024年02月08日
    浏览(46)
  • 数据结构--》解锁数据结构中树与二叉树的奥秘（二）

    数据结构--》解锁数据结构中树与二叉树的奥秘（二）

            数据结构中的树与二叉树，是在建立非线性数据结构方面极为重要的两个概念。它们不仅能够模拟出生活中各种实际问题的复杂关系，还常被用于实现搜索、排序、查找等算法，甚至成为一些大型软件和系统中的基础设施。         无论你是初学者还是进阶者，

    2024年02月08日
    浏览(43)
  • 【数据结构与算法】之8道顺序表与链表典型编程题心决！

    【数据结构与算法】之8道顺序表与链表典型编程题心决！

                                                                                    个人主页：秋风起，再归来~                                                                                             数据结构与算

    2024年04月14日
    浏览(59)
  • 【Python数据结构与算法】线性结构小结

    【Python数据结构与算法】线性结构小结

    🌈个人主页: Aileen_0v0 🔥系列专栏:PYTHON学习系列专栏 💫\\\"没有罗马,那就自己创造罗马~\\\"   目录 线性数据结构Linear DS 1.栈Stack 栈的两种实现 1.左为栈顶,时间复杂度为O(n) 2.右为栈顶,时间复杂度O(1)   2.队列Queue 3.双端队列Deque 4.列表List 5.链表 a.无序链表的实现 b.有序链表的实

    2024年02月04日
    浏览(42)
  • Python数据结构与算法-数据结构(列表、栈、队列、链表)

    Python数据结构与算法-数据结构(列表、栈、队列、链表)

    数据结构是指相互之间存在这一种或者多种关系的数据元素的集合和该集合中元素之间的关系组成。 简单来说，数据结构就是设计数据以何种方式组织并存储在计算机中。 比如：列表、集合与字典等都是一种数据结构。 N.Wirth:“程序=数据结构+算法” 数据结构按照其 逻辑结

    2024年02月08日
    浏览(58)

  • python数据结构和算法

    参考 python图解算法 选择/快速排序 哈希表 广度优先搜索算法 迪杰斯特拉算法 贪婪算法 动态规划 K-邻近算法 算法计时 time模块，与算法复杂度 O() [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EIwk2Zdi-1691788469064)(https://facert.gitbooks.io/python-data-str

    2024年02月13日
    浏览(50)
  • Python数据结构与算法

    Python数据结构与算法

    栈、队列、双端队列和列表都是有序的数据集合， 其元素的顺序取决于添加顺序或移除顺序。一旦某个元素被添加进来，它与前后元素的相对位置将保持不变。这样的数据集合经常被称为线性数据结构。 栈的添加操作和移除操作总发生在同一端。栈中的元素离底端越近，代

    2024年02月02日
    浏览(55)
  • Python数据结构与算法-树

    Python数据结构与算法-树

    详情见 https://blog.csdn.net/little_limin/article/details/129845592 Python数据结构与算法-堆排序（NB组）—— 一、树的基础知识 树结构也是链式存储的，与链表的结构相似，只是树存在多个子节点，不是线性的，存在一堆多的情况。与双链表相似，只不过链表节点对应的下一个节点只有一

    2023年04月15日
    浏览(37)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包