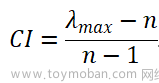层次分析法简介
层次分析法(Analytic Hierarchy Process,AHP)是一种多准则决策方法,用于解决复杂的决策问题。它是由美国数学家托马斯·萨亚基(Thomas L. Saaty)于20世纪70年代提出的。其基本思想是将复杂的决策问题分解为层次结构,通过对准则和方案进行定量和定性的比较,最终得出最佳决策。层次结构由准则层、子准则层和方案层组成,准则层表示决策问题的目标和标准,子准则层表示实现目标的具体要素,方案层表示可选的决策方案。在AHP中,通过构建判断矩阵来比较准则和方案之间的重要性。判断矩阵是一个方阵,其中每个元素表示两个准则或方案之间的比较结果。通过对准则和方案进行两两比较,可以得到判断矩阵。然后,通过计算判断矩阵的特征向量,可以得出准则和方案的权重,用于进行综合决策。在进行判断矩阵的构建和权重计算时,AHP还考虑了一致性的问题。一致性是指比较结果的合理性和稳定性。AHP通过计算一致性指标和一致性比率来检验判断矩阵的一致性,确保比较结果的可靠性。AHP可以应用于各种决策问题,例如项目选择、投资决策、供应商选择、产品评估等。它提供了一种系统化和结构化的方法,帮助决策者在面对复杂的决策问题时做出明智的选择。
题目举例
请为大学毕业的青年建立一个选择志愿的层次结构模型.
解题步骤
Ⅰ、建立层次结构
首先对题目进行问题分析并搜索多方面资料对问题进行回答。
1.为什么要选择志愿?(目标层)
为同学选择最合适的发展路线。
2.有什么因素影响志愿选择?(准则层)
经济情况、学习情况、兴趣情况、性格情况、家庭情况。
3.选择的志愿类型有哪些?(方案层)
工作、考公、读研、创业。
建立层次结构图如下:
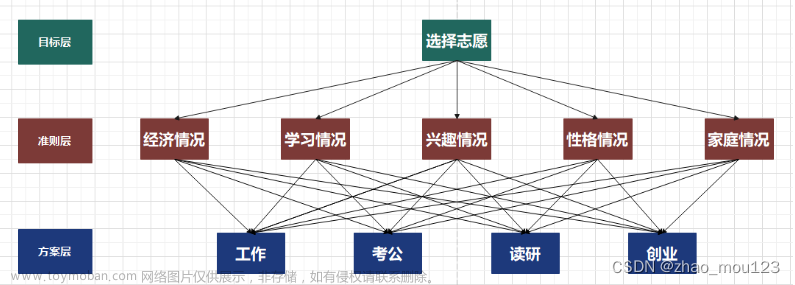
图1-1 层次结构图
Ⅱ、构造判断矩阵
我们的解题目标为填写出权重表格。
假设各准则之间相互独立。

图2-1 权重表格
通过进行各准则与各方案的关系判断矩阵求出权重比例。构造空白目标判断矩阵如下:

图2-2 判断矩阵O-C
空白处为各准则之间的比例关系。通过简单的分治策略可以轻松求出。这里以经济和学习进行举例。
eg:
重要程度表如下:

图2-3 重要程度表
根据重要程度表进行专家判断得出判断矩阵如下:

图2-4 判断矩阵O-C
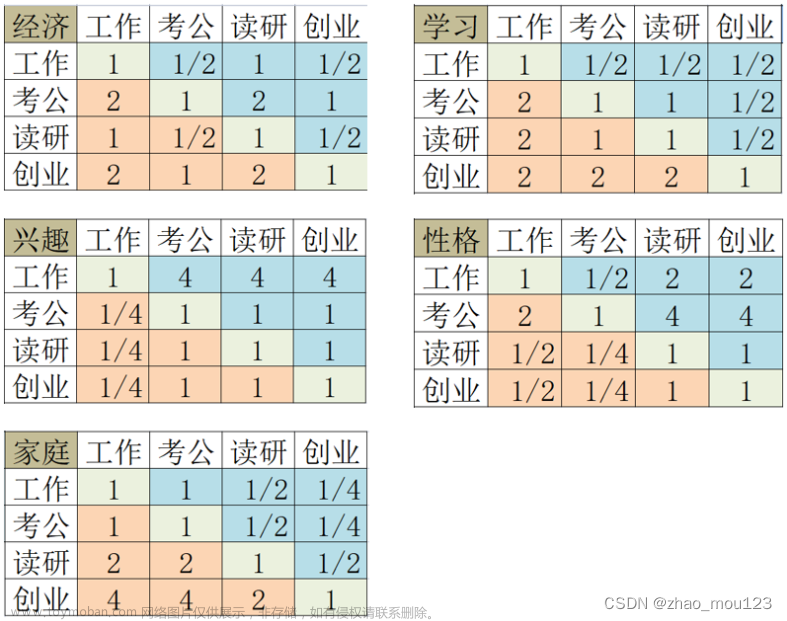
图2-5 判断矩阵C-P
Ⅲ、一致性检验
对所有判断矩阵进行一致性检验通过后才能进行求权重。
首先需要了解两个概念:
①矩阵中的所有元素均大于0且满足Aij*Aji=1,即正互反矩阵。
②在正互反矩阵中满足Aij*Ajk=Aik,即一致矩阵。
以图2-5中C1-P举例,当i=1,j=2,k=4时:

图3-1 判断矩阵C1-P

即①条件满足。

*一致矩有一个特征值为n,其余为0。

即②条件满足。
接下来进行一致性检验:
1.计算一致性指标CI

其中:n为矩阵的阶,λmax为矩阵最大特征值。
clear;clc
disp('判断矩阵A: ')
A = [1 1/2 2 1 2;
2 1 4 2 1;
1/2 1/4 1 1/2 1/4;
1 1/2 2 1 1/2;
1/2 1 4 2 1]
[row,col] = size(A);
[V,D] = eig(A);
% 求最大特征值
MAX_D = max(max(D));
CI = (MAX_D - row) / (row - 1)CI = 0.0613
2.查找对应的平均随机一致性指标RI

平常n大多小于10,如果超过10可以考虑建立二级指标体系。
3.计算一致性比例CR

如果CR<0.1,则可认为判断矩阵的一致性可以接受,否则需要对判断矩阵进行修正。
clear;clc
disp('判断矩阵A: ')
A = [1 1/2 2 1 2;
2 1 4 2 1;
1/2 1/4 1 1/2 1/4;
1 1/2 2 1 1/2;
1/2 1 4 2 1]
[row,col] = size(A);
[V,D] = eig(A);
% 求最大特征值
MAX_D = max(max(D));
CI = (MAX_D - row) / (row - 1);
CR = CI / 1.12
if CR < 0.1
disp('True')
else
disp('False')
endCR = 0.0548 True
Ⅳ、合成权重
权重合成方法有三种:算数平均值法、几何平均值法、特征值法。
1.算数平均值法
clear;clc
disp('判断矩阵A: ')
A = [1 1/2 2 1 2;
2 1 4 2 1;
1/2 1/4 1 1/2 1/4;
1 1/2 2 1 1/2;
1/2 1 4 2 1]
%% 方法1:算术平均法求权重
% 第一步:将判断矩阵按照列归一化(每一个元素除以其所在列的和)
Sum_col_A = sum(A);
% 求出A的行列大小
[row,col] = size(A);
% 构造出中间矩阵
Temp_A = repmat(Sum_col_A,row,1);
clc;
% 得出答案
Stand_A = A ./ Temp_A;
% 这里我们直接将两个矩阵对应的元素相除即可
% 第二步:将归一化的各列相加
Stand_SUM_A = sum(Stand_A,2);
% 第三步:将得到的向量点除阶数得到权重
ans_A = Stand_SUM_A ./ row;
ans_A.'
% 检验求出的矩阵和是否为一,为一表示正确
if sum(ans_A) == 1
disp("True")
else
disp("False")
end// 得出权重 ans_A.' = [0.2165 0.3067 0.0767 0.1534 0.2467]
2.几何平均值法
clear;clc
disp('判断矩阵A: ')
A = [1 1/2 2 1 2;
2 1 4 2 1;
1/2 1/4 1 1/2 1/4;
1 1/2 2 1 1/2;
1/2 1 4 2 1]
%% 方法2:几何平均法求权重
% 第一步:将A的元素按照行相乘得到一个新的列向量
Prduct_A = prod(A,2)
% 第二步:将新的向量的每个分量开n次方
% 求出A的行列大小
[row,col] = size(A);
Prduct_row_A = Prduct_A .^ (1/row)
% 第三步:对该列向量进行归一化即可得到权重向量
% 即将这个列向量中的每一个元素除以这一个向量的和
ans_A = Prduct_row_A ./ sum(Prduct_row_A)
% 检验求出的矩阵和是否为一,为一表示正确
if sum(ans_A) == 1
disp("True")
else
disp("False")
end// 得出权重 ans_A.' = [0.2083 0.3157 0.0789 0.1578 0.2393]
3.特征值法
clear;clc
disp('判断矩阵A: ')
A = [1 1/2 2 1 2;
2 1 4 2 1;
1/2 1/4 1 1/2 1/4;
1 1/2 2 1 1/2;
1/2 1 4 2 1]
%% 方法3:特征值法
% 第一步:求出矩阵A的最大特征值以及其对应的特征向量
[V,D] = eig(A);
MAX_D = max(max(D));
[r,c] = find(D == MAX_D,1);
% 第二步:对求出的特征向量进行归一化即可得到我们的权重
ans_A = V(:,1) ./ sum(V(:,1))
% 检验求出的矩阵和是否为一,为一表示正确
if sum(ans_A) == 1
disp("True")
else
disp("False")
end// 得出权重 ans_A.' = [0.2223 0.3059 0.0765 0.1530 0.2424]
Ⅴ、得出权重表
根据判断矩阵和准则权重得出答案。
clear;clc;
% 三种方法得出的权重矩阵
weight_1 = [0.2165 0.3067 0.0767 0.1534 0.2467];
weight_2 = [0.2083 0.3157 0.0789 0.1578 0.2393];
weight_3 = [0.2223 0.3059 0.0765 0.1530 0.2424];
% C-P矩阵
C1 = [1 1/2 1 1/2;
2 1 2 1;
1 1/2 1 1/2;
2 1 2 1;];
C2 = [1 1/2 1/2 1/2;
2 1 1 1/2;
2 1 1 1/2;
2 2 2 1;];
C3 = [1 4 4 4;
1/4 1 1 1;
1/4 1 1 1;
1/4 1 1 1;];
C4 = [1 1/2 2 2;
2 1 4 4;
1/2 1/4 1 1;
1/2 1/4 1 1;];
C5 = [1 1 1/2 1/4;
1 1 1/2 1/4;
2 2 1 1/2;
4 4 2 1;];
% 求权重
disp('算数平均值求解答案:')
C1_weight = C1(:,1) .* weight_1;
C1_weight = C1_weight(:,1)
C2_weight = C2(:,1) .* weight_1;
C2_weight = C2_weight(:,1)
C3_weight = C3(:,1) .* weight_1;
C3_weight = C3_weight(:,1)
C4_weight = C4(:,1) .* weight_1;
C4_weight = C4_weight(:,1)
C5_weight = C5(:,1) .* weight_1;
C5_weight = C5_weight(:,1)
disp('几何平均值求解答案:')
C1_weight = C1(:,1) .* weight_2;
C1_weight = C1_weight(:,1)
C2_weight = C2(:,1) .* weight_2;
C2_weight = C2_weight(:,1)
C3_weight = C3(:,1) .* weight_2;
C3_weight = C3_weight(:,1)
C4_weight = C4(:,1) .* weight_2;
C4_weight = C4_weight(:,1)
C5_weight = C5(:,1) .* weight_2;
C5_weight = C5_weight(:,1)
disp('特征值求解答案:')
C1_weight = C1(:,1) .* weight_3;
C1_weight = C1_weight(:,1)
C2_weight = C2(:,1) .* weight_3;
C2_weight = C2_weight(:,1)
C3_weight = C3(:,1) .* weight_3;
C3_weight = C3_weight(:,1)
C4_weight = C4(:,1) .* weight_3;
C4_weight = C4_weight(:,1)
C5_weight = C5(:,1) .* weight_3;
C5_weight = C5_weight(:,1)根据答案填写权重表。文章来源:https://www.toymoban.com/news/detail-799137.html
 文章来源地址https://www.toymoban.com/news/detail-799137.html
文章来源地址https://www.toymoban.com/news/detail-799137.html
到了这里,关于数学建模:层次分析法(AHP)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!