DDPM:去噪扩散概率模型
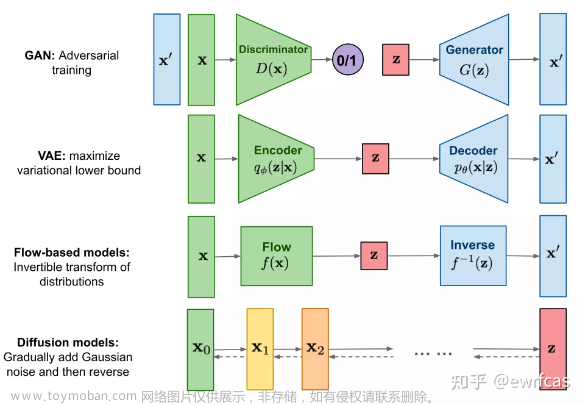
ddpm是一类生成模型,其工作原理是逐渐向数据中添加噪声,然后学习如何逆转这一过程。这个想法是通过一个称为扩散的过程将一个简单的分布(通常是高斯噪声)转换成一个复杂的数据分布(如图像或音频),然后反向生成新的样本。
简单的过程可以描述如下:
- 从数据分布中的数据示例 x 0 x_0 x0开始。
- 通过一系列步骤将噪声添加到该数据样本 t t t以生成 x t x_t xt,最终变为纯噪声。
- 训练一个神经网络来逆转这个过程,即去噪,从 x T x_T xT(纯噪声)回到 x 0 x_0 x0(数据样本)。
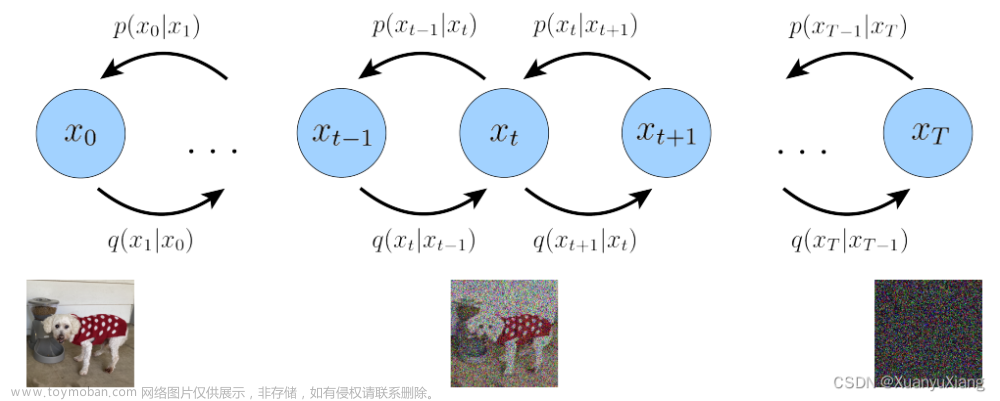
正向扩散过程可以用马尔可夫链来描述:
x t = 1 − β t x t − 1 + β t ϵ , ϵ ∼ N ( 0 , I ) x_{t} = \sqrt{1 - \beta_t} x_{t-1} + \sqrt{\beta_t} \epsilon, \quad \epsilon \sim \mathcal{N}(0, I) xt=1−βtxt−1+βtϵ,ϵ∼N(0,I)
式中$ \beta_t 为方差调度参数, 为方差调度参数, 为方差调度参数, \epsilon $为高斯噪声。
相反的过程,也就是模型所学到的,可以简化为:
x t − 1 = f ( x t , t ; θ ) x_{t-1} = f(x_t, t; \theta) xt−1=f(xt,t;θ)
其中 f f f是一个由 θ \theta θ参数化的神经网络,它学习对 x t x_t xt去噪以估计 x t − 1 x_{t-1} xt−1。
DDIM:去噪扩散隐式模型
ddim是ddpm的非马尔可夫变体,允许更快的采样,并可以提供确定性输出。关键思想是,它们改变了逆向过程的计算方式,在不牺牲质量的情况下,允许更少的步骤生成样本。
在ddim中,反向过程被修改,以便每个步骤都可能撤销多个正向扩散步骤。反向过程可表述为:
x t − 1 = α t − 1 f ( x t , t ; θ ) + 1 − α t − 1 ϵ t , ϵ t ∼ N ( 0 , I ) x_{t-1} = \sqrt{\alpha_{t-1}} f(x_t, t; \theta) + \sqrt{1 - \alpha_{t-1}} \epsilon_t, \quad \epsilon_t \sim \mathcal{N}(0, I) xt−1=αt−1f(xt,t;θ)+1−αt−1ϵt,ϵt∼N(0,I)这里, α t − 1 \alpha_{t-1} αt−1是控制学习到的去噪函数 f f f和添加的噪声 ϵ t \epsilon_t ϵt之间权衡的系数。DDPM和DDIM反向过程之间的关键区别在于DDIM的确定性设置,其中 ϵ t \epsilon_t ϵt是从模型派生出来的,创建了从 x T x_T xT到 x 0 x_0 x0的确定性路径。
ddim可以被认为是一种更有效地遍历扩散过程的方法,通常会导致更快的推理时间,因为它们可以采取更大的步骤而不会引入太多错误。
我们尝试进一步简化ddpm和ddim的解释:
DDPM:去噪扩散概率模型
想象一下,你有一张清晰的照片(你的原始数据),你开始在许多小步骤中添加一点随机噪声。每一步,照片都变得更加混乱,直到它完全是随机的噪音。ddpm学习如何做相反的事情:从噪音开始,他们弄清楚如何一步一步地消除噪音,以恢复原始的清晰照片。
用数学术语来说,你可以这样考虑每个增加噪声的步骤:
x
noisy
=
x
clear
+
noise
x_{\text{noisy}} = x_{\text{clear}} + \text{noise}
xnoisy=xclear+noise
而ddpm学会做相反的事情,就像:
x
less noisy
=
some process to remove noise from
x
noisy
x_{\text{less noisy}} = \text{some process to remove noise from } x_{\text{noisy}}
xless noisy=some process to remove noise from xnoisy
DDIM:去噪扩散隐式模型
现在,对于ddimm,这个想法是类似的,但是ddimm不是在许多步骤中去除一点点噪声,而是找到了一种方法,只需几个步骤就可以去除大量噪声。因此,它们可以更快地清除有噪点的照片,因为它们每次都在清除噪点方面有更大的飞跃。
简单来说,他们学习的反向过程更像是:
x
less noisy
=
a more effective noise removal process applied to
x
noisy
x_{\text{less noisy}} = \text{a more effective noise removal process applied to } x_{\text{noisy}}
xless noisy=a more effective noise removal process applied to xnoisy
ddpm和ddim之间的区别主要在于它们如何逆转噪声添加过程。ddpm通过许多小步骤来完成,而ddim通过更少、更大的步骤来完成。这使得ddimm能够更快地从噪声中生成清晰的图像,因为它们可以走捷径,而不需要经过每一个小步骤就能获得清晰的图像。
总而言之,ddpm就像一丝不苟地一块一块地清理脏窗户,而ddim就像把整个窗户擦几次,让它变得一样干净。
DDPM(去噪扩散概率模型)
在DDPM中,在每个反向步骤中,网络将噪声图像$ x_t 和时间步长 和时间步长 和时间步长 t 作为输入,并预测已添加到原始图像中的噪声 作为输入,并预测已添加到原始图像中的噪声 作为输入,并预测已添加到原始图像中的噪声 \epsilon 以到达 以到达 以到达 x_t $。逆扩散过程在每一步的公式为:
x t − 1 = 1 α t ( x t − 1 − α t 1 − α ˉ t ϵ ^ θ ( x t , t ) ) + σ t ⋅ z x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \hat{\epsilon}_\theta(x_t, t) \right) + \sigma_t \cdot z xt−1=αt1(xt−1−αˉt1−αtϵ^θ(xt,t))+σt⋅z
其中$ \hat{\epsilon}_\theta(x_t, t) 是神经网络预测的噪声, 是神经网络预测的噪声, 是神经网络预测的噪声, z $是一个随机噪声向量,如果需要可以添加(用于随机抽样)。
DDIM(去噪扩散隐式模型)
DDIM使用相同的神经网络来预测噪声$ \epsilon $。然而,反向过程的表述不同,以允许非马尔可夫动力学和更大的步骤。DDIM中反向步骤的公式为:
x t − 1 = α ˉ t − 1 ( x t − 1 − α ˉ t ⋅ ϵ ^ θ ( x t , t ) α ˉ t ) + 1 − α ˉ t − 1 − σ t 2 ⋅ ϵ ^ θ ( x t , t ) + σ t ⋅ z x_{t-1} = \sqrt{\bar{\alpha}_{t-1}} \left( \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \cdot \hat{\epsilon}_\theta(x_t, t)}{\sqrt{\bar{\alpha}_t}} \right) + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \cdot \hat{\epsilon}_\theta(x_t, t) + \sigma_t \cdot z xt−1=αˉt−1(αˉtxt−1−αˉt⋅ϵ^θ(xt,t))+1−αˉt−1−σt2⋅ϵ^θ(xt,t)+σt⋅z
在这个公式中,$ \hat{\epsilon}_\theta(x_t, t) 同样是神经网络的输出。术语 同样是神经网络的输出。术语 同样是神经网络的输出。术语 \sigma_t 是该步骤所选择的噪声级别, 是该步骤所选择的噪声级别, 是该步骤所选择的噪声级别, z $是一个随机噪声向量,可以将其设置为零以使该过程具有确定性。
说明
在这两种情况下,只有一个网络可以预测噪声$ \epsilon $。DDPM和DDIM之间的关键区别在于它们如何在反向过程中使用预测的噪声和其他术语来重建原始图像。由于其公式,DDIM可以在反向过程中进行更大的跳跃,这使得它比DDPM更有效,DDPM需要更小、更渐进的步骤。文章来源:https://www.toymoban.com/news/detail-799342.html
网络$ \theta 预测 预测 预测 \epsilon ,但是它用于计算下一个 ,但是它用于计算下一个 ,但是它用于计算下一个 x_{t-1} $的方式在DDPM和DDIM之间是不同的,DDIM允许一个非马尔可夫过程,它可以通过扩散过程向后采取可变大小的步骤。文章来源地址https://www.toymoban.com/news/detail-799342.html
到了这里,关于【扩散模型】DDPM,DDIM的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!