Python时间序列分析–ARIMA模型实战案例,利用ARIMA模型对时间序列进行分析的经典案例(详细代码)
**本文将介绍使用Python来完成时间序列分析ARIMA模型的完整步骤与流程,绘制时序图,平稳性检验,单位根检验,白噪声检验,模型定阶,参数估计,模型检验等完整步骤。Python建立时间序列分析–ARIMA模型实战案例时间序列指的是将带有同一指标单位的数值按照产生时间的先后顺序排成的数列,对时间序列分析的主要目的是对目前已有的数据对未来进行预测。本文将使用将差分移动自回归模型(ARIMA)来对中国区域CH4浓度未来变化趋势做预测。
步骤:
(1) 首先判断时间序列数据是否平稳,若平稳,则进行下一步,若不平稳,就通
过差分处理将序列变为平稳,为保证数据的准确性,差分次数应该不超过2。
(2) 判断时间序列是否是白噪声序列,如果是白噪声序列,那么该不序列并不适合ARIMA 模型分析,若不是,则进行下一步。
(3) 模型定阶,通过自相关函数 ACF 和偏自相关函数 PACF 来决定模型的阶数
P、Q,也可以通过Bayesian Information Criterion(贝叶斯信息量BIC)准则来确定。
(4) 建模并进行残差分析和白噪声检验。
(5) 对时间序列数据使用训练完成的 ARIMA 模型进行预测,并对差分的数据进
行还原。
参考文章:
https://blog.csdn.net/qq_45176548/article/details/111504846#comments_14302892
https://blog.csdn.net/weixin_41013322/article/details/111221251
https://blog.csdn.net/u010414589/article/details/49622625
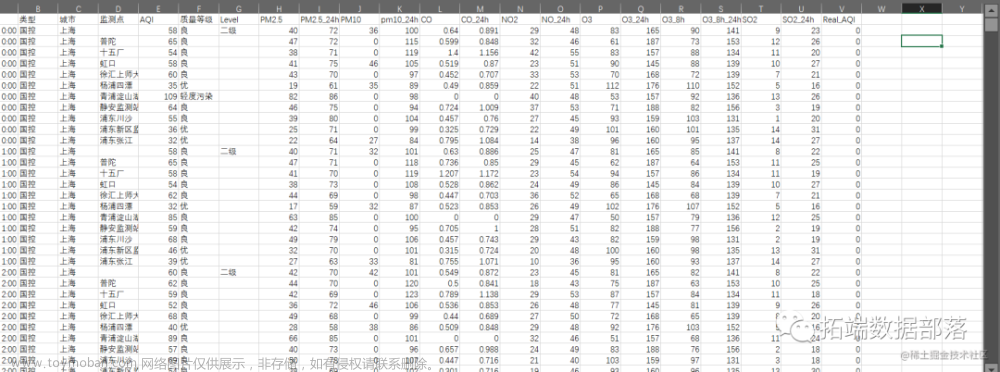
所用csv文件形式,只用这一列即可。
- 第一步导包
import decimal
import sys
import os
import statsmodels
from math import sqrt
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
import warnings
import seaborn as sns
import matplotlib as matplotlib
import math
import matplotlib
from keras.losses import mean_squared_error, mean_absolute_error
from pasta.augment import inline
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
from arch.unitroot import ADF
import matplotlib.pylab as plt
# %matplotlib inline
from matplotlib.pylab import style
style.use('ggplot')
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.tsa.stattools import adfuller
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.graphics.api import qqplot
pd.set_option('display.float_format', lambda x: '%.5f' % x)
np.set_printoptions(precision=5, suppress=True)
"""中文显示问题"""
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
pd.set_option('display.width', 10000)
- 导入csv文件
这里是将CSV文件与python代码放在同一目录下,data1为一阶差分的序列
data = pd.read_csv('LSTM-01.csv',parse_dates=True)
dc=data["ch4"]
data1 = data["ch4"].diff(1)
data1.dropna(inplace=True)
print(data.head())
- 检查平稳性
ADF 单位根检验法是一种严格的统计检验方法,原理是指时间序列中是否存在单位根,如果是非平稳序列则存在单位根,反之是平稳序列则不存在单位根。本研究中使用ADF单位根检验法。
print("原始单位根检验:\n")
print(ADF(data["ch4"].dropna())) #原始
- 检查平稳性
这里结果求得p值为0.995,大于0.05,可以直接判定该序列为非平稳序列
然后对其进行一阶差分,再使用ADF检验
P 值为 0.002,远小于0.05,并且 Τ 统计量都小于 1%,5%,10%的临界值,可以直接判定该序列为平稳序列,符合时间序列模型。确定d=1
data["diff1"] = data["ch4"].diff(1).dropna()
print("一阶单位根检验:\n")
print(ADF(data.diff1.dropna())) #一阶

- 判断是不是非白噪声序列,前一步的平稳性检验证明了该序列是平稳的,下面要判断该序列是否是白噪声序列,白噪声序列是没有研究意义的。所以需要对该序列进行白噪声检验,保证该序列是有研究意义的。白噪声检验结果的 P 值均小于0.05,可以判定该时序序列为非白噪声序列。
from statsmodels.stats.diagnostic import acorr_ljungbox
lb=acorr_ljungbox(data["ch4"].diff(1).dropna(), lags = [i for i in range(1,12)],boxpierce=True)
print("白噪声检验")
print(lb)

- 建立ARIMA模型,求得合适P,Q值
建立 ARIMA 模型首先要确定模型阶数,也就是要确定(P,D,Q)的值,在前一步已经确定差分次数为 1,所以 D 的值为 1。为找到适合模型的最佳阶数 P,Q 的值,将通过BIC 信息准则来进行判断。
data1为一阶差分的序列
train_results = sm.tsa.arma_order_select_ic(data1, ic=['aic', 'bic'], max_ar=4, max_ma=4)
print('AIC', train_results.aic_min_order)
print('BIC', train_results.bic_min_order)

- ARIMA 模型的检验
确定了模型之后,要对拟合的模型进行检验,主要是对模型的显著性检验,检验模型的有效性,一个良好的模型的观察值序列中的样本信息应该是一个纯随机序列,即白噪声序列。如果残差序列是白噪声序列,说明序列中已经剔除了能对预测结果产生干扰的因素,残差序列就是不想关的,相反,如果不是白噪声序列,残差序列相关可能会造成预测结果的失真。
德宾-沃森(Durbin-Watson)检验。德宾-沃森检验,简称D-W检验,是目前检验自相关性最常用的方法,但它只使用于检验一阶自相关性。因为自相关系数ρ的值介于-1和1之间,所以 0≤DW≤4。并且DW=O=>ρ=1 即存在正自相关性
DW=4<=>ρ=-1 即存在负自相关性
DW=2<=>ρ=0 即不存在(一阶)自相关性
因此,当DW值显著的接近于O或4时,则存在自相关性,而接近于2时,则不存在(一阶)自相关性。这样只要知道DW统计量的概率分布,在给定的显著水平下,根据临界值的位置就可以对原假设H0进行检验。
首先观察连续残差是否(自)相关,进行D-W检验。求得DW的值为#1.0077473271396427说明不存在自相关性。
print('dwwwwwwwwwwww的值为')
print(sm.stats.durbin_watson(result.resid.values))
LB检验
Ljung-Box test是对randomness的检验,或者说是对时间序列是否存在滞后相关的一种统计检验。对于滞后相关的检验,我们常常采用的方法还包括计算ACF和PCAF并观察其图像,但是无论是ACF还是PACF都仅仅考虑是否存在某一特定滞后阶数的相关。LB检验则是基于一系列滞后阶数,判断序列总体的相关性或者说随机性是否存在。
时间序列中一个最基本的模型就是高斯白噪声序列。而对于ARIMA模型,其残差被假定为高斯白噪声序列,所以当我们用ARIMA模型去拟合数据时,拟合后我们要对残差的估计序列进行LB检验,判断其是否是高斯白噪声,如果不是,那么就说明ARIMA模型也许并不是一个适合样本的模型。
r,q,p = sm.tsa.acf(resid.values.squeeze(), qstat=True)
print(r[1:])
print('---------')
print(q)
print('-------p值为--')
print(p)
print('ssssss')
统计量的 P 值大于 0.05 的显著性水平,通过了显著性检验,结果说明 ARIMA(3,1,2),模型的残差序列为白噪声序列,模型显著有效
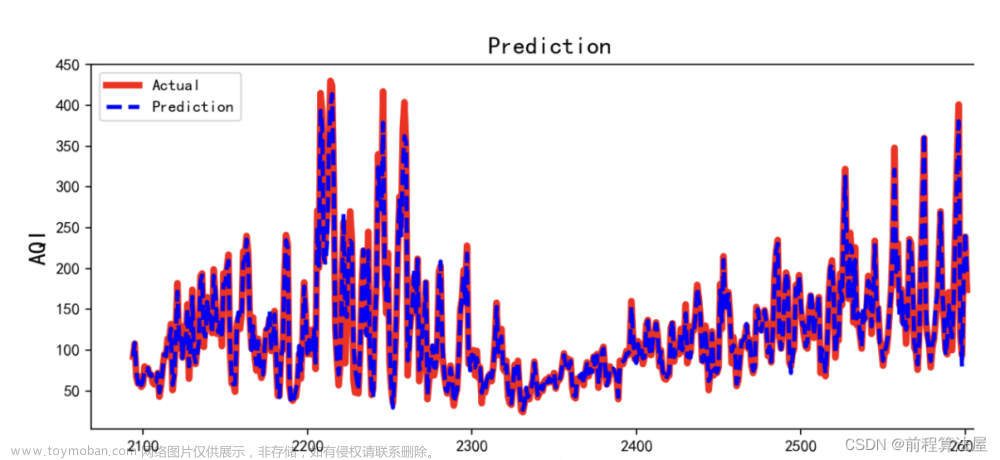
- 模型预测
利用ARIMA模型进行预测,预测已有的228个数据,预测未来的200个数据。
model1 = sm.tsa.ARIMA(data1, order=(3, 1, 2)) # 传入参数,构建并拟合模型
result=model1.fit()
predict_data = result.predict(0, 227) # 预测数据
print('预测数据')
print(predict_data)
forecast_data = result.forecast(200) # 预测未来数据
```bash
绘制图像文章来源:https://www.toymoban.com/news/detail-799356.html
plt.plot(dc, label='原数据')
plt.plot(predict_data, label='预测数据')
plt.plot(forecast_data, label='未来数据')
plt.legend()
plt.show()
print('----------预测未来值')
print(forecast_data)
以下可以求一些用于评价模型标准的值文章来源地址https://www.toymoban.com/news/detail-799356.html
# calculate MSE 均方误差
mse=mean_squared_error(dc,pred)
# calculate RMSE 均方根误差
rmse = math.sqrt(mean_squared_error(dc,pred))
#calculate MAE 平均绝对误差
mae=mean_absolute_error(dc,pred)
#calculate R square
r_square=r2_score(dc,pred)
print('均方误差MSE: %.6f' % mse)
print('均方根误差RMSE: %.6f' % rmse)
print('平均绝对误差MAE: %.6f' % mae)
print('R_square: %.6f' % r_square)
11.
到了这里,关于Python时间序列分析--ARIMA模型实战案例的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!