自动驾驶中的坐标系
0.引言
总结于网络。重点在世界坐标系理解。
图自
图自
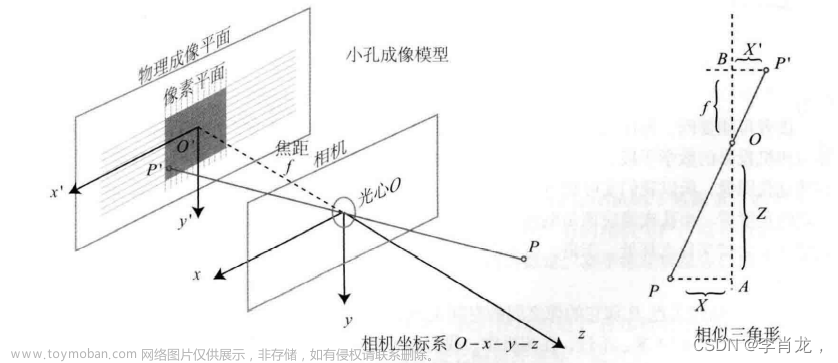
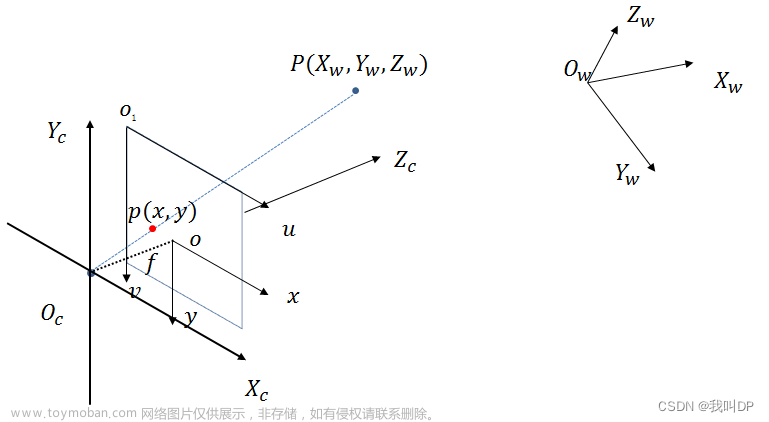
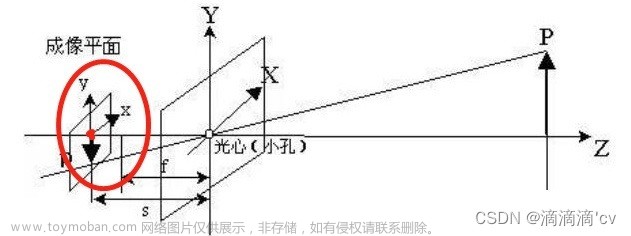
1.相机传感器坐标系
针孔模型:

图自
2.激光雷达坐标系
Velodyne生产的64线激光雷达HDL64:
64线激光雷达进行环境扫描过程:单帧扫描数据
64线激光雷达进行环境扫描过程:全周扫描数据
激光雷达坐标系统

此节来自
3.车体坐标系
车体坐标系用来描述车辆周围的物体和本车之间的相对位置关系。目前学术界和工业界有几种比较常用的车体坐标系定义方式。分别是ISO国际标准定义,SAE(Society of Automotive Engineers)汽车工程师协会定义,和基于惯性测量单元IMU的坐标定义。
在车辆动力学分析中,ISO定义的车体坐标系较为常见。SAE定义的车体坐标系与航空航天领域常用的机体坐标系相一致。基于IMU定义的车体坐标系,则在IMU的相关应用中较为常见。
此节来自
4.世界坐标系

地理坐标系统(英文简写GCS,Geographical Coordinate System)地理坐标系单位 度°分’秒"–>擅长定位
投影坐标系统(英文简写PCS,Projection Coordinate System)投影坐标系单位 米m–>擅长计算
4.1.地理坐标系

图自
某官网
大地坐标系与地理坐标系有何不同?
大地坐标系和地理坐标系都是经纬度表示的坐标系,本身并不包含投影信息,很多时候,这两种说法都是相同的。

蓝色:实际地球
红色:地心坐标系–>全球拟合表达
绿色:参心坐标系–>局部拟合表达(对于局部精度更高!)
大地坐标系(经纬度)
L:longitude -->经度
B:latitude -->纬度
H: altitude -->海拔height above sea level
0度经线:国际上将通过英国伦敦格林尼治天文台原址的那条经线称为0°经线,也叫本初子午线:分别向东向西从 0°到 180°
0度纬线:赤道,越往两极纬度越高。纬线在南北极缩成一个点,叫极点,也分别是90°纬线。
表述:东经、西经、南纬、北纬–>"E"东经、"W"西经、"N"北纬、"S"南纬–>平时一般使用东经和北纬(也即是以东经北纬方向为正)

WGS84坐标系,全称为世界大地测量系统(英语:World Geodetic System)。WGS包含一套地球的标准经纬坐标系、一个用于计算原始海拔数据的参考椭球体,和一套用以定义海平面高度的引力等势面数据。WGS-84坐标为GPS(经过差分后)测量出来的,属于大地坐标系。
4.2.投影坐标系
4.2.1.投影方式



4.2.2.墨卡托(Mercator)投影

墨卡托(Mercator)投影,是一种"等角正切圆柱投影”.墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
图自
4.2.3.高斯-克吕格(Gauss-Kruger)投影
1.高斯-克吕格投影
高斯-克吕格(Gauss-Kruger)投影简称“高斯投影”,又名"等角横切椭圆柱投影”,地球椭球面和平面间正形投影的一种。投影后,除中央子午线和赤道为直线外, 其他子午线均为对称于中央子午线的曲线。投影在长度和面积上变形很小,中央经线无变形,自中央经线向投影带边缘,变形逐渐增加(为什么会有变形,想象橘子皮剥开后压平),变形最大之处在投影带内赤道的两端。
2.高斯-克吕格投影分带
按照经线每隔多少度(三分度,六分度)进行划分:三分度:每隔三度一个中央经线(360/3 =120条中央子午线)
无带号坐标:
有带号坐标:
 三度带变形小,覆盖区域小
三度带变形小,覆盖区域小
六度带变形大,覆盖区域大
4.2.4.通用横轴墨卡托UTM(UniversalTransverseMercator)投影
和高斯克吕格投影非常相似,只不过它并不是切于经线圈,而是穿地球而过。我们从侧面来看,高斯投影面和经线圈是完全重合的,但是UTM则不是:
UTM投影现在采用WGS84地理坐标系统进行投影。
UTM投影全称为“通用横轴墨卡托投影”,是等角横轴割圆柱投影(高斯-克吕格为等角横轴切圆柱投影),圆柱割地球于南纬80度、北纬84度两条等高圈,该投影将地球划分为60个投影带,每带经差为6度,已被许多国家作为地形图的数学基础。UTM投影与高斯投影的主要区别在南北格网线的比例系数上添加链接描述,高斯-克吕格投影的中央经线投影后保持长度不变,即比例系数为1,而UTM投影的比例系数为0.9996。UTM投影沿每一条南北格网线比例系数为常数,在东西方向则为变数,中心格网线的比例系数为0.9996,在南北纵行最宽部分的边缘上距离中心点大约 363公里,比例系数为 1.00158。
高斯-克吕格投影与UTM投影可近似采用 Xutm=0.9996 * X高斯,Yutm=0.9996 * Y高斯进行坐标转换。
UTM
坐标3度带与6度带的知识01
坐标3度带与6度带的知识02
中央子午线
6度带中央子午线计算公式:当地经度/6=N;中央子午线L=6 X N
当没有除尽,N有余数时,中央子午线L=6 X N - 3
3度带中央子午线计算公式:当地经度/3=N;中央子午线L=3 X N
顺带知识点:
全球分为二十四个时区,以能够被15整除的经度作为该区域的中央子午线,每一时区占经度15度。
在该时区中央子午线以东的地区,时间要加,以西的地区,时间要减,一度4分钟。
中国共分五个时区:
(1)中原时区:以东经120度为中央子午线。
(2)陇蜀时区:以东经105度为中央子午线。
(3)新藏时区:以东经90度为中央子午线。
(4)昆仑时区:以东经75(82.5)度为中央子午线。
(5)长白时区:以东经135(127.5)度为中央子午线。
一个时区的“标准时”,只是一个大地区的统一时间,大家共同遵守的“人工”时间而已,并不是该时区内每个地点的“本地时间(LMT)”——真正的经度时。要用出生地的经度与出生大地区的标准时来加减,全球任何地点都用这个原则。
例如:中原时区包括内蒙古、辽宁、河北、山西、山东、河南、安徽、江苏、湖北、湖南、江西、浙江、福建、广东、海南、香港、澳门、台湾。这个大地区当时钟敲定正午12点时,只有位于东经120度线上的地点才是12点,其它的地方是少于或多于12点。如香港位于东经114度10分,比东经120度偏西5度50分,其真正经度时是11时36分40秒。

4.3.WGS84与UTM相互转换
UTM与WGS84相互转换
在每个纵向区域内,横向墨卡托投影用于给出以米为单位的坐标(东距和北距)。
对于东距,原点定义为每个纵向带中央子午线以西 500,000 米的点,给出中央子午线的东距 500,000 米。
对于北半球的北向,原点被定义为赤道。
对于南半球的北向,原点定义为赤道以南 10,000,000 米的点。
X轴:指向东边
Y轴:指向北边
Z轴:指向天顶
将中央子午线指定为每个区域内坐标系的参考 y 轴(即东距 = 0)将导致中央子午线以西的点的东距值为负。为此,中央子午线被指定为 500000 米的任意值,从而避免任何负东坐标;位于其东面的点的东距值将大于 500000m,位于西面的点的值将小于 500000m。此分配会将原点放置在中央子午线以西 500000m 的区域外,因此原点称为假原点,东坐标称为假东。
赤道被指定为 UTM 北向坐标的水平参考轴,并为北半球的区域分配了 0 米北的值。为了避免负数,赤道被分配了一个10,000,000米南的假北距,用于参考南半球的北距坐标。(但是好像图中没有给出假北距)
UTM - 通用横轴墨卡托
UTM坐标和WGS84坐标
UTM的东北坐标只有两个数字,还需要zone的区间号才能转换为经纬度坐标因此准确的UTM坐标包括三个参数,区间+东北坐标。
GPS经纬度坐标转UTM坐标(c++)
void LonLat2UTM(double longitude, double latitude, double& UTME, double& UTMN)
{
double lat = latitude;
double lon = longitude;
double kD2R = PI / 180.0;
double ZoneNumber = floor((lon - 1.5) / 3.0) + 1;
double L0 = ZoneNumber * 3.0;
double a = 6378137.0;
double F = 298.257223563;
double f = 1 / F;
double b = a * (1 - f);
double ee = (a * a - b * b) / (a * a);
double e2 = (a * a - b * b) / (b * b);
double n = (a - b) / (a + b);
double n2 = (n * n);
double n3 = (n2 * n);
double n4 = (n2 * n2);
double n5 = (n4 * n);
double al = (a + b) * (1 + n2 / 4 + n4 / 64) / 2.0;
double bt = -3 * n / 2 + 9 * n3 / 16 - 3 * n5 / 32.0;
double gm = 15 * n2 / 16 - 15 * n4 / 32;
double dt = -35 * n3 / 48 + 105 * n5 / 256;
double ep = 315 * n4 / 512;
double B = lat * kD2R;
double L = lon * kD2R;
L0 = L0 * kD2R;
double l = L - L0;
double cl = (cos(B) * l);
double cl2 = (cl * cl);
double cl3 = (cl2 * cl);
double cl4 = (cl2 * cl2);
double cl5 = (cl4 * cl);
double cl6 = (cl5 * cl);
double cl7 = (cl6 * cl);
double cl8 = (cl4 * cl4);
double lB = al * (B + bt * sin(2 * B) + gm * sin(4 * B) + dt * sin(6 * B) + ep * sin(8 * B));
double t = tan(B);
double t2 = (t * t);
double t4 = (t2 * t2);
double t6 = (t4 * t2);
double Nn = a / sqrt(1 - ee * sin(B) * sin(B));
double yt = e2 * cos(B) * cos(B);
double N = lB;
N = N + t * Nn * cl2 / 2;
N = N + t * Nn * cl4 * (5 - t2 + 9 * yt + 4 * yt * yt) / 24;
N = N + t * Nn * cl6 * (61 - 58 * t2 + t4 + 270 * yt - 330 * t2 * yt) / 720;
N = N + t * Nn * cl8 * (1385 - 3111 * t2 + 543 * t4 - t6) / 40320;
double E = Nn * cl;
E = E + Nn * cl3 * (1 - t2 + yt) / 6;
E = E + Nn * cl5 * (5 - 18 * t2 + t4 + 14 * yt - 58 * t2 * yt) / 120;
E = E + Nn * cl7 * (61 - 479 * t2 + 179 * t4 - t6) / 5040;
E = E + 500000;
N = 0.9996 * N;
E = 0.9996 * (E - 500000.0) + 500000.0;
UTME = E;
UTMN = N;
}
GPS坐标转换:经纬度转UTM坐标(Matlab程序)
感悟:没有系统的学习,去网上查资料都是零碎的业余选手讲解,很难形成系统,所以有时间还是需要多读书,但是也不知道这个知识点在那本书中有详细的讲解,就像这篇博客下面的评论一样,想问问是那本书上的公式都没人理。
根据经纬度算UTM带号
UTM是由美国制定,因此起始分带并不在本初子午线,而是在180度,因而所有美国本土都处于0-30带内。UTM投影采用6度分带,从东经180度(或西经180度)开始,自西向东算起,因此1带的中央经线为-177(-180 -(-6)),而0度经线为30带和31带的分界,这两带的分界分别是-3和3度。纬度采用8度分带,从80S到84N共20个纬度带(X带多4度),分别用C到X的字母来表示。为了避免和数字混淆,I和O没有采用。UTM的“false easting”值为500km,而南半球UTM带的“false northing”为10000km
“WGS 1984”坐标系的墨卡托投影分度带(UTM ZONE)选择方法如下:
(1)北半球地区,选择最后字母为“N”的带;
(2)可根据公式计算,带数=(经度整数位/6)的整数部分+31
如:北京经度约116.4,
带数=116/6+31=50,选50N,即WGS 1984 UTM ZONE 50N
GPS定位技术
apollo 采用的UTM投影
- 根据经度求带号
namespace {
int GetLongZone(double longitude) {
double longZone = 0.0;
if (longitude < 0.0) {
longZone = ((180.0 + longitude) / 6.0) + 1;
} else {
longZone = (longitude / 6.0) + 31;
}
return static_cast<int>(longZone);
}
}
5.自动驾驶中的坐标定位
GPS/RTK获得经度lon、纬度lat、高程height、偏航角yaw、俯仰角pitch、横滚角roll 。
将lon,lat转化为utm坐标,(utm_x, utm_y, height)就可以作为GPS此时在世界坐标系下位置,再把yaw,pitch,roll转化为旋转矩阵,就可以得到GPS在世界坐标系下的姿态q,合起来就得到了GPS在世界坐标系下的位姿
通过标定可得到GPS到车身base_link坐标系的变换,这样就能得到当前车身base_link在世界坐标系下的位姿,再由标定可得到lidar到车身base_link坐标系的变换,这样就能把lidar坐标系下的点云变换到世界坐标系下,也就是高精地图中点云的坐标。
由于地图太大,需要对其进行方形网格分块进行存储和查询,每一块的id可通过resolution, col(utm_x/resolution), row(utm_y/resolution), utm_zone, utm_band进行编码。
同时,将GPS得到的经纬度转换为火星坐标系 (在中国大陆使用地图服务的话,我们可能会看到GCJ-02这个坐标系统,这又是什么东西呢?GCJ-02是国家测绘局(国测局,GCJ,这样的缩写比较罕见)02号标准的意思。它是一种对经纬度数据的加密算法,即加入随机的偏差。国内出版的各种地图系统(包括电子形式),必须至少采用GCJ-02对地理位置进行首次加密。由于最开始的时候一些国外地图服务商没搞明白这点,直接使用了GCJ-02加密的坐标来显示POI,从而把这些POI移到太平洋上去了,所以网友也戏称火星坐标。) ,就通过一些地理信息可视化库在地图上可视化轨迹,如通过轨迹坐标生成kml文件,就可以在谷歌地球上显示轨迹。文章来源:https://www.toymoban.com/news/detail-799391.html
整篇文章转载自文章来源地址https://www.toymoban.com/news/detail-799391.html
到了这里,关于自动驾驶中的坐标系的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!