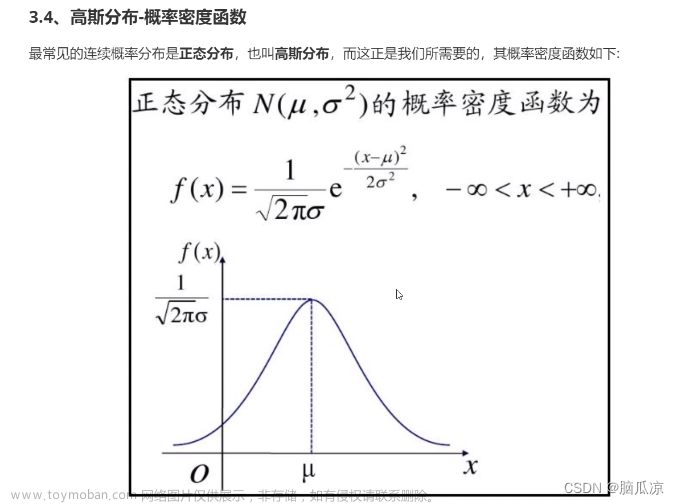
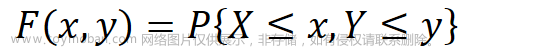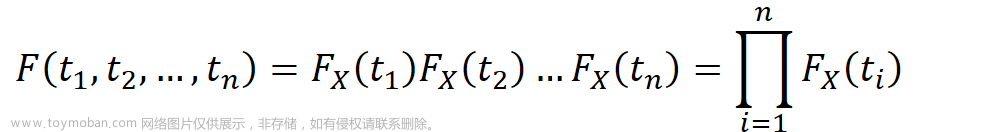对数高斯分布-Toy模板网

这篇具有很好参考价值的文章主要介绍了对数高斯分布。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

对数高斯分布是指服从正态分布的随机变量经过取对数变换后得到的分布。具体地，设 $X\sim N(\mu,\sigma^2)$ 为一个正态分布随机变量， $Y=\ln(X)$ 则 $Y$ 服从对数高斯分布，即 $Y\sim\mathcal{LN}(\mu,\sigma^2)$ 。
设 $X\sim N(\mu,\sigma^2)$ 为一个正态分布随机变量， $Y=\ln(X)$ 则 $Y$ 服从对数高斯分布，即 $Y\sim\mathcal{LN}(\mu,\sigma^2)$ 。那么 $Y$ 的均值和方差可以如下计算：

均值：

$E(Y)=E(\ln(X))=\int_{-\infty}^\infty \ln(x) \cdot \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx$ 根据对数高斯分布的定义，我们可以将 $x=e^y$ 带入上式中得到： $E(Y)=E(\ln(X))=\int_{-\infty}^\infty y \cdot \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(e^y-\mu)^2}{2\sigma^2}}dy$ 由于此处无法对积分式子进行解析求解，所以我们无法得到 $Y$ 的均值的显式表达式，但是可以使用数值计算方法进行求解。
常用的数值积分算法有梯形法、辛普森法和高斯积分法等。其中，辛普森法是一种较为常用的数值积分方法，其基本思路是将被积函数分段逼近为二次多项式，然后对每一段进行积分。下面是使用辛普森法计算对数高斯分布的均值E(Y)的示例MATLAB代码：

% 定义对数高斯分布的均值和方差
mu = 1; 
sigma = 0.5; 

% 定义被积函数
f = @(y) y .* lognpdf(y, mu, sigma);

% 定义积分上下限和分段数
a = 0;
b = 10;
n = 10000;

% 使用辛普森法计算积分
x = linspace(a, b, n+1);
y = f(x);
S = (b-a) / (3*n) * (y(1) + 4*sum(y(2:2:end-1)) + 2*sum(y(3:2:end-2)) + y(end));

% 输出对数高斯分布的均值
EY = exp(S)

其中，lognpdf(y, mu, sigma)表示对数高斯分布的概率密度函数，linspace(a, b, n+1)表示在区间[a, b]上均匀地生成n+1个点。

方差：

$\mathrm{Var}(Y)=E(Y^2)-(E(Y))^2$ 同样利用 $x=e^y$ 的关系，我们有： $Y^2=\ln^2(X)=(\ln X)^2$ 所以 $E(Y^2)=E((\ln X)^2)=\int_{-\infty}^\infty (\ln x)^2 \cdot \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx$ 我们可以通过对上式进行两次分部积分，得到： $E(Y^2)=\mu^2+\sigma^2$ 于是，对数高斯分布的方差为： $\mathrm{Var}(Y)=\mu^2+\sigma^2-(E(Y))^2$ 文章来源地址https://www.toymoban.com/news/detail-799572.html