目录
一.引言
二.位运算简介
1.二进制与十进制
2.左/右移
3.位运算
4.异或 XOR
5.指定位置的位运算
6.实战要点
三.经典算法实战
1.Number-1-of-bits [191]
2.Power-Of-Two [231]
3.Reverse-2-Bits [190]
4.N-Queens [51]
四.总结
一.引言
通常情况下我们计数采取十进制,这是因为日常生活中我们习惯了 0-9 的数字习惯,而对于计算机而言,其通过 0-1 的二进制方式表示和存储数字。本节开始我们学习二进制以及其对应的位运算。
二.位运算简介
1.二进制与十进制
机器中数字的表示和存储格式就是二进制,给定数字 0101 其等于从后向前:
即对应位置的索引作为 2 的指数,对应位置的值作为指数幂的系数,累加即为 10 进制的数字。

相反的,如果想把一个 10 进制的数字转换为 2 进制,则我们依次除 2 取余,把得到的数字反转即可得到其二进制。这里不好理解的话可以对照着上面 10 进制转 2 进制的公式再思考思考。上面的图片来自: wikihow,是一个很好玩的百科网站,大家可以去搜索你想了解的内容。
2.左/右移

左移右移就是把当前二进制数字向左或向右移动一个位置,空出来的位置补 0 ,被顶出去的位置就不要了。我们老式的计算机一般是采用 32 位表示,而新的计算机则都采用了 64 位表示。
3.位运算

- 按位或 有一个 1,则或出来就是 1
- 按位与 有一个 0 ,则与出来就是 0
- 按位取反 0 变成 1,1 变成 0
- 按位异或 相同为 0,不同为 1
以上位运算都是在两个二进制数字之间展开。
4.异或 XOR

这里 1s 代表全为 1,即把 0 取反 ~0。 后面两条定律使用的比较少,前面四条性质比较常用。
5.指定位置的位运算

上面给出了一些位运算常见的位置操作,用于我们处理对应位置的位数。
6.实战要点

判断奇偶以及 /2 的常规操作,我们都可以改写为位运算的方式提高效率,除此之外通过 & 方法可以得到清除、得到最低位 1 的操作。
三.经典算法实战
1.Number-1-of-bits [191]
位1的个数: https://leetcode.cn/problems/number-of-1-bits/description/

◆ 题目分析
& 操作是, 1 & x = x,所以我们可以遍历 32 位数的每一位 & 1 的值,如果为 1 则说明该位为 1,则 cnt += 1,或者使用上面实战要点中 X = X & (X-1) 清零最低位 1 的操作,能清几次代表有几个 1。
◆ 1 & x = x
class Solution(object):
def hammingWeight(self, n):
"""
:type n: int
:rtype: int
"""
cnt = 0
for i in range(32):
if n & (1 << i):
cnt += 1
return cnt
◆ x & (x-1)
class Solution(object):
def hammingWeight(self, n):
"""
:type n: int
:rtype: int
"""
cnt = 0
while n:
n = n & (n-1)
cnt += 1
return cnt
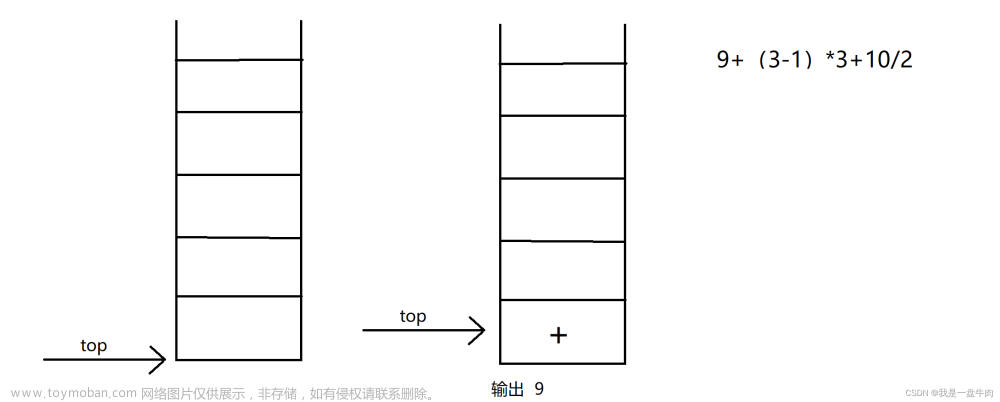
n & (n-1) 的示意图可以参考上面的过程。

2.Power-Of-Two [231]
2的幂: https://leetcode.cn/problems/power-of-two/description/

◆ 题目分析
套用上面的 1 bits 方法,由于2的幂次一定只有 1 位有 1,所以判断 cnt 是否为 1 即可。也可以一直 % 2 并 / 2,看能不能一直除下去。
◆ x & (x-1)
class Solution(object):
def isPowerOfTwo(self, n):
"""
:type n: int
:rtype: bool
"""
if n == 0:
return False
return n & (n-1) == 0
◆ x % 2 - x / 2
class Solution(object):
def isPowerOfTwo(self, n):
"""
:type n: int
:rtype: bool
"""
if n == 1:
return True
if n <= 0 or n % 2:
return False
return self.isPowerOfTwo(n / 2)
3.Reverse-2-Bits [190]
颠倒 2 进制: https://leetcode.cn/problems/reverse-bits/description/

◆ 题目分析
把 n 的 32 位,每一位拿出来再往后追加,类似于一位一位 reverse。
◆ x << 1
class Solution:
# @param n, an integer
# @return an integer
def reverseBits(self, n):
res = 0
for i in range(32):
# 有 1 就 1,没 1 就 0
res = (res << 1) | (n & 1)
n >>= 1
return resres << 1: 把最后一位空出来
n & 1: 0 是 0、1 是 1
|: 前面 res 部分不动,后面 0 是 0、1 是 1
通过这三部分实现反转与追加。

4.N-Queens [51]
N 皇后: https://leetcode.cn/problems/n-queens/description/

◆ 题目分析
老生常谈的问题了, 传统的办法我们是构造了 pie、na、row 三个 set 进行去重,学习了位运算后,我们也可以将棋盘按 45 度划分 2n-1 个对角线,这样 pie、na 就只需要位运算判重而不需要 set 了,提高了空间利用率和时间效率。
◆ DFS + Set
class Solution(object):
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
results = []
# 行 左 右 是否可以放置
cols = set()
pie = set()
na = set()
def dfs(n, row, cur):
if row >= n:
results.append(cur)
for col in range(n):
if col in cols or (row + col) in pie or (row - col) in na:
continue
# 判断有效
cols.add(col)
pie.add(row + col)
na.add(row - col)
dfs(n, row + 1, cur + [col])
# 恢复状态
cols.remove(col)
pie.remove(row + col)
na.remove(row - col)
dfs(n, 0, [])
return self.genResult(n, results)
def genResult(self, n, results):
return [[ '.' * i + 'Q' + (n - i - 1) * '.' for i in result] for result in results]
def genResultV2(self, n, results):
re = []
for result in results:
re.append([ '.' * i + 'Q' + (n - i - 1) * '.' for i in result])
return re

◆ DFS + Simple Set
class Solution(object):
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
results = []
def dfs(queue, diff, total):
row = len(queue)
if row == n:
results.append(queue)
return None
for col in range(n):
if col not in queue and row + col not in total and row - col not in diff:
dfs(queue + [col], diff + [row - col], total + [row + col])
dfs([], [], [])
return [[ '.' * i + 'Q' + (n - i - 1) * '.' for i in result] for result in results]

◆ DFS + Bit
class Solution(object):
def power_of_two(self, num):
power = 0
while num % 2 == 0:
power += 1
num = num / 2
return power
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
if n < 1:
return []
results = []
def DFS(n, row, cols, pie, na, cur):
if row >= n:
results.append(cur)
return
# 得到当前所有空位
bits = (~(cols | pie | na) & ((1 << n) - 1))
while bits:
p = bits & -bits # 取最低位的 1
bits = bits & (bits - 1) # P 位置放置皇后
DFS(n, row + 1, cols | p, (pie | p) << 1, (na | p) >> 1, cur + [p])
DFS(n, 0, 0, 0, 0, [])
return [['.' * self.power_of_two(i) + 'Q' + (n - self.power_of_two(i) - 1) * '.' for i in result] for result in results]这里 bits 以及一些递进的操作直接看容易懵,大家可以在 n=4 的情况下,打印每一次运算的 2 进制,感受下如何通过位运算求解,这里可以通过 bin() 方法获取二进制表示。
 文章来源:https://www.toymoban.com/news/detail-799662.html
文章来源:https://www.toymoban.com/news/detail-799662.html
四.总结
位运算的解法和题目相对来说比较抽象,不理解的时候还是多转换为 2 进制数字,查看其演进的过程,更好的熟悉其推导过程。文章来源地址https://www.toymoban.com/news/detail-799662.html
到了这里,关于Python - 深夜数据结构与算法之 位运算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!