深度学习
必备的数学知识
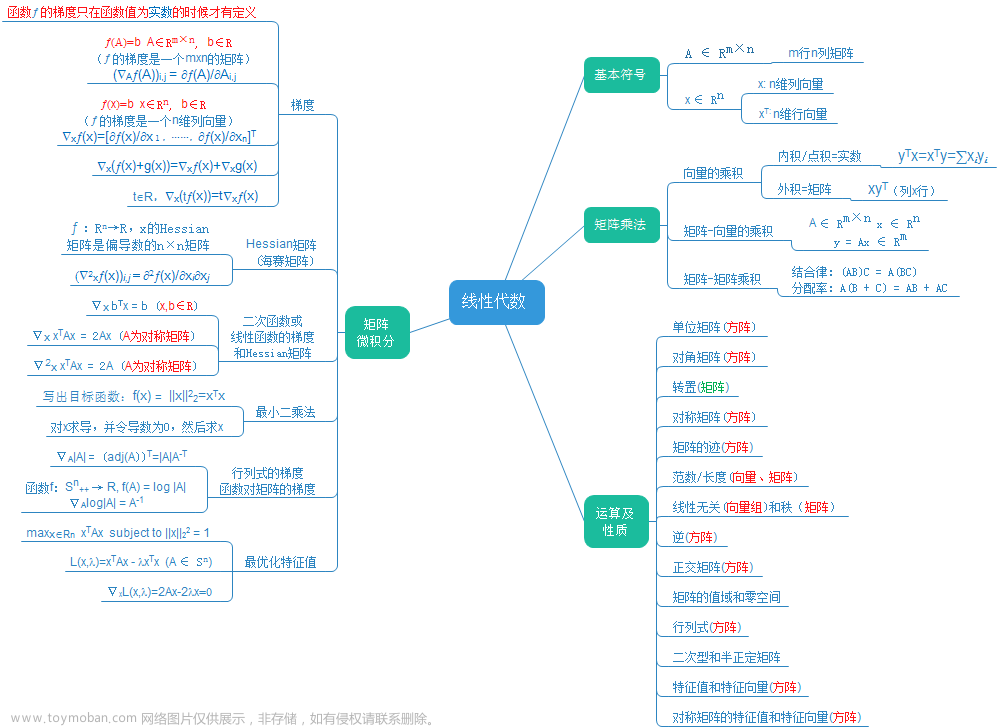
线性代数
通过伪逆求解线性方程组
伪逆,又称为Moore-Penrose逆,它是一种广义的矩阵。我们可以找到任意一个矩阵的伪逆。矩阵
A
\mathbf{A}
A的伪逆定义为:
A
+
=
lim
x
→
0
(
A
T
A
+
α
I
)
−
1
A
T
\mathbf{A}^+=\lim_{x \to 0}(\mathbf{A}^T\mathbf{A}+\alpha\mathbf{I})^{-1}\mathbf{A}^T
A+=x→0lim(ATA+αI)−1AT
这个公式被称为Tikhonov正则化,或岭回归。计算矩阵伪逆的方法很多, 这是其中的一种。我们还可以通过奇异值(SVD)计算伪逆。
A
+
=
V
D
+
U
T
\mathbf{A}^+=\mathbf{V}\mathbf{D}^+\mathbf{U}^T
A+=VD+UT
其中
V
D
U
\mathbf{V} \mathbf{D} \mathbf{U}
VDU分别对应于奇异值分解中的三个矩阵。
- V \mathbf{V} V是右奇异向量组成的矩阵
- D + \mathbf{D}^+ D+是 D \mathbf{D} D的伪逆,是一个以奇异值为对角元素的对角矩阵。对角矩阵的伪逆是通过取原矩阵的对角线上元素的倒数得到的
- U \mathbf{U} U是左奇异向量组成的矩阵
对于一个 m × n m \times n m×n的矩阵 A \mathbf{A} A,其伪逆 A + \mathbf{A}^+ A+是一个 n × m n \times m n×m的矩阵, A + \mathbf{A}^+ A+满足以下四个条件:
- A A + A = A \mathbf{A}\mathbf{A}^+\mathbf{A}=\mathbf{A} AA+A=A
- A + A A + = A + \mathbf{A}^+\mathbf{A}\mathbf{A}^+=\mathbf{A}^+ A+AA+=A+
- ( A + A ) T = A + A (\mathbf{A}^+\mathbf{A})^T=\mathbf{A}^+\mathbf{A} (A+A)T=A+A
- ( A A + ) T = A A + (\mathbf{A}\mathbf{A}^+)^T=\mathbf{A}\mathbf{A}^+ (AA+)T=AA+
在求解线性方程
A
x
=
y
\mathbf{A}\mathbf{x}=\mathbf{y}
Ax=y时,如果
A
\mathbf{A}
A是可逆的,那么我们可以通过
x
=
A
−
1
b
\mathbf{x}=\mathbf{A}^{-1}\mathbf{b}
x=A−1b
来求解,但是并不是每一个矩阵都存在逆矩阵。对于不可以使用矩阵逆求解的方程,我们可以使用伪逆进行求解。
伪逆的一个重要性质是
A
A
+
A
=
A
\mathbf{A}\mathbf{A}^+\mathbf{A}=\mathbf{A}
AA+A=A,
所以
A
x
=
b
A
A
+
A
x
=
A
A
+
b
A
x
=
A
A
+
b
x
=
A
+
b
\mathbf{A}\mathbf{x}=\mathbf{b}\\ \mathbf{A}\mathbf{A}^+\mathbf{A}\mathbf{x}=\mathbf{A}\mathbf{A}^+\mathbf{b}\\ \mathbf{A}\mathbf{x}=\mathbf{A}\mathbf{A}^+\mathbf{b}\\ \mathbf{x}=\mathbf{A}^+\mathbf{b}
Ax=bAA+Ax=AA+bAx=AA+bx=A+b
x
=
A
+
b
\mathbf{x}=\mathbf{A}^+\mathbf{b}
x=A+b的解是满足
∣
∣
A
x
−
b
∣
∣
2
||\mathbf{A}\mathbf{x}-\mathbf{b}||_2
∣∣Ax−b∣∣2最小的解,换句话说
x
=
A
+
b
\mathbf{x}=\mathbf{A}^+\mathbf{b}
x=A+b的解是方程所有可行性解中欧几里得距离
∣
∣
x
∣
∣
2
||x||_2
∣∣x∣∣2最小的一个
迹运算
迹运算是线性代数中的一种运算, 它对应的是一个方程所有主对角线元素的和:
T
r
(
A
)
=
∑
i
A
i
,
i
Tr({\mathbf{A}})=\sum_{i}A_{i,i}
Tr(A)=i∑Ai,i
迹运算有着很多重要的性质。
对于任意方阵
A
\mathbf{A}
A和
B
\mathbf{B}
B
T
r
(
A
+
B
)
=
T
r
(
A
)
+
T
r
(
B
)
Tr(\mathbf{A}+\mathbf{B})=Tr(\mathbf{A})+Tr(\mathbf{B})
Tr(A+B)=Tr(A)+Tr(B)
对于任意方阵
A
\mathbf{A}
A和标量c
T
r
(
c
A
)
=
c
T
r
(
A
)
Tr(\mathbf{c\mathbf{A}})=cTr(\mathbf{A})
Tr(cA)=cTr(A)
标量的迹运算结果仍然是它自身
T
r
(
a
)
=
a
Tr(a)=a
Tr(a)=a
矩阵的迹运算结果等同于矩阵逆的迹运算结果
T
r
(
A
)
=
T
r
(
A
T
)
Tr(\mathbf{A})=Tr(\mathbf{A}^T)
Tr(A)=Tr(AT)
对一组矩阵乘积进行迹运算得到的迹与将这组矩阵的最后一个移至最前面之后相乘的迹是相同(要保证在移动后,矩阵乘积仍然成立)
T
r
(
A
B
.
.
N
)
=
T
r
(
N
A
B
.
.
)
Tr(\mathbf{A}\mathbf{B}..\mathbf{N})=Tr(\mathbf{N}\mathbf{A}\mathbf{B}..)
Tr(AB..N)=Tr(NAB..)
更一般的
T
r
(
∏
i
=
1
n
F
(
i
)
)
=
T
r
(
F
(
n
)
∏
i
=
1
n
−
1
F
(
i
)
)
Tr(\prod_{i=1}^{n}\mathbf{F}^{(i)})=Tr(\mathbf{F}^{(n)}\prod_{i=1}^{n-1}\mathbf{F}^{(i)})
Tr(i=1∏nF(i))=Tr(F(n)i=1∏n−1F(i))
迹运算还提供了描述矩阵Frobenius范式的方式:
∣
∣
A
∣
∣
F
=
T
r
(
A
A
T
)
||A||_{F}=\sqrt{Tr(\mathbf{A}\mathbf{A}^T)}
∣∣A∣∣F=Tr(AAT)
行列式
矩阵特征值的乘积称为行列式,记作
d
e
t
(
A
)
det(A)
det(A)或
∣
A
∣
|\mathbf{A}|
∣A∣。
行列式有着许多重要的性质和应用:文章来源:https://www.toymoban.com/news/detail-799980.html
- 行列式可以帮助我们判断一个矩阵是否可逆,如果一个矩阵的行列式为0,那么这个矩阵是不可逆的,如果一个矩阵的行列式不为0,那么这个矩阵是可逆的
- 行列式可以用来计算一个矩阵的伪逆
- 等等
如有问题 恳请指正
持续更新中…文章来源地址https://www.toymoban.com/news/detail-799980.html
到了这里,关于深度学习-必备的数学知识-线性代数6的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!