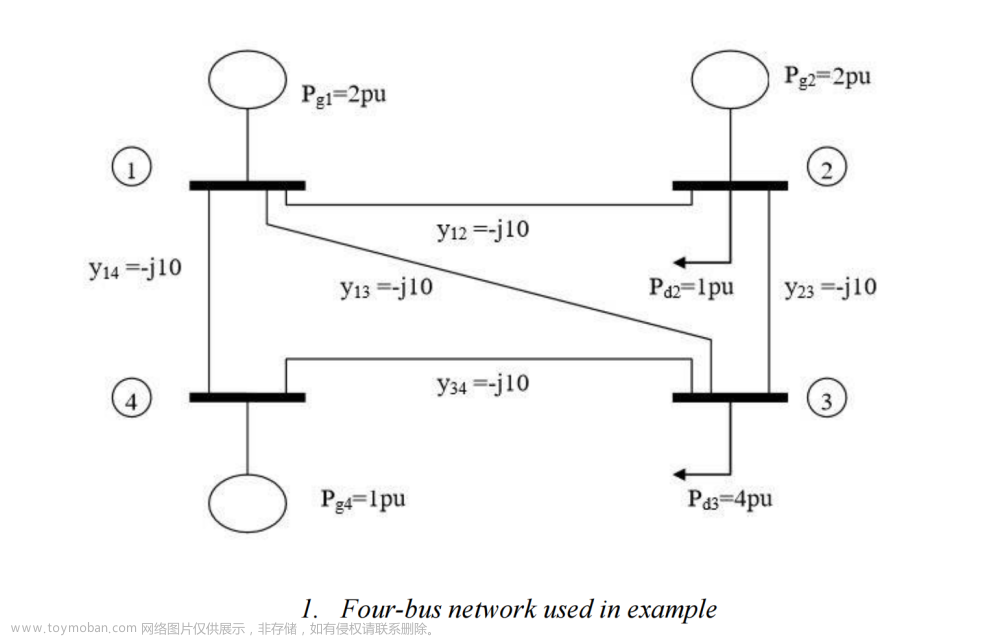
一、分别运用雅克比、高斯-赛德尔两种迭代方法计算如下方程:

解:由于系数方程组不满足严格行(列)对角优矩阵的条件,即迭代不收敛,故将方程组转化成以下形式:

(一)Jacobi迭代法:
迭代方程可以化为:

得迭代矩阵:

可以在Matlab编写出以下迭代程序,创建脚本函数文件名为Jacobi_solve.m:

创建好函数文件之后,新建脚本,输入
A: 线性方程组的系数矩阵(n*n,非奇异)
b: 方程组右边的常数项列向量
n: 方程组维数
x0: 初始值
tol: 精度上限值
N: 最大迭代次数
调用函数Jacobi_solve.m:

在命令窗口可以看出,当取:

时,得:

查看程序结果验证:


依次收敛下去,雅可比迭代12次,得出程序精确解:

(二)Gauss_Seidel迭代法:
迭代方程可以化为:

得迭代矩阵:

可以在Matlab编写出以下迭代程序,创建名为Gauss_Seidel_solve.m:

创建好函数文件之后,在方法一得基础上,输入量不变,注释掉调用Jacobi_solve,更改调用函数Gauss_Seidel_solve.m:,运行函数,观察命令窗口出现具体迭代过程:

此时,在命令窗口可以看出,当取:

时,得:

继续迭代:

依次收敛迭代下去:

在命令行窗口可以看出,高斯—赛德尔迭代只需要迭代8次,比雅可比迭代快,程序精确解为:

二、采用牛顿-拉夫逊方法求解方程的根:xe^x-1=0

解:初步判断:当x=0时,y=-1<0,当x=1时,y=e-1>0,函数在[0,1]内方程有解,在指令窗口输入x=0:0.0001:1,确定好横坐标的范围后,观察函数在坐标系中的具体图像:

由上图可以看出函数y在坐标系中的图线,可以看到过零点在0.5-0.6之间,图中发现过零点在0.567附件。我们可以在matlab中新建脚本,按照牛顿拉夫逊求解方程法编写好函数之后,创建函数文件名为newton.m,对函数进行精确求解(程序如下):

在函数图像的基础上求导函数,精度为0.0001,继续编写调用newton(),取x=0.5,0.5710时,画出函数切线,观察验证迭代过程趋向:

将箭头中黑色框部分放大观察一次,二次导函数切线过零点:

验证结果发现,函数的二次导切线过零点已经非常趋向于函数的真解,因此:一共迭代3次即可得出函数精确解:文章来源:https://www.toymoban.com/news/detail-800146.html
x=0.5671文章来源地址https://www.toymoban.com/news/detail-800146.html
到了这里,关于电力系统分析常用的三种迭代方法(雅克比、高斯赛德尔、牛顿拉夫逊法)求解方程的精确解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!