NSGA-II 遗传多目标算法（python示例）

一、前言

        最近在准备毕业论文，研究了一下主流的多目标算法，对于NSGA-II，网上大部分代码是全部是面向过程来实现的，本人更喜欢采用面向对象的方式，故采用python面向对象实现了一个示例，实现了对于二元多目标问题的求解。

二、算法基本流程

三、核心思想

1、非支配排序

这个简单的例子说明了帕累托最优的概念。上面我们有4个成员A, B, C和D，有两个特征:身高和工资。现在，如果我们同时比较他们的身高和薪水，我们会发现这不是很直观，因为他们有多个目标。

既然这两个目标越大越好，我们可以简单地对它们进行比较。首先，我们观察到A和B都比C和D多，所以我们说A和B在身高和薪水上“支配”C和D。同理，C支配D，D可被A,B,C支配。

A和B呢?A比B高，但是工资低。相反，B面临着同样的情况。我们称这种情况为“非支配”。 如果我们能找到一组解它们不互相支配，也不受其他解支配，我们称之为"帕累托最优"解。在上面的例子中，A和B都在帕累托最优前沿。

几个概念：

非支配解：假设任何二解S1 及S2 对所有目标而言，S1均优于S2，则我们称S1 支配S2，若S1 的解没有被其他解所支配，则S1 称为非支配解（不受支配解），也称Pareto解（帕雷托解）

支配解：若解S2的所有目标均劣于S1，则称S1优于S2，也称S1支配S2，S2为受支配解。

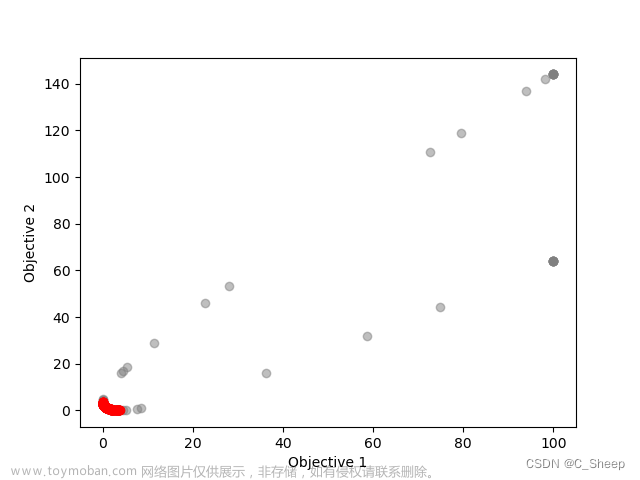
Pareto前沿面：找到所有Pareto解之后，这些解组成的平面叫做Pareto前沿面（Non-dominated front）。在目标函数较多时，前沿面通常为超曲面。

2、拥挤度

通俗的来讲，当需要舍弃某一rank平面的部分节点时，由于同一平面中的所有节点rank相同，不能通过rank来舍弃，而是要通过拥挤度来舍弃，以上就是拥挤度的作用。

算法更倾向于稀疏的点，也就是让节点更可能的分散，可以有效地方式早熟和过拟合现象

3、精英选择策略

每次都将父类与子类想结合，依次采用非支配排序、计算拥挤度来选择父代。

四、python实现

github:   源代码地址文章来源地址https://www.toymoban.com/news/detail-800569.html

"""
author: pym
time: 2023.10.29
ide: pycharm2
"""

from collections import defaultdict
import numpy as np
import random
import matplotlib.pyplot as plt
import math

class Individual(object):
    def __init__(self):
        self.solution = None    # 实际为nparray类型，方便四则运算
        self.objective = defaultdict()

        self.n = 0              # 解p被几个解支配
        self.rank = 0           # 解p所在层数
        self.S = []             # 解p支配解的集合
        self.distance = 0       # 拥挤度距离

    def bound_process(self, bound_min, bound_max):
        """
        对解向量 solution 中的每个分量进行定义域判断；超过最大值赋为最大值
        :param bound_min: 定义域下限
        :param bound_max: 定义域上限
        :return:
        """
        for i, item in enumerate(self.solution):
            if item > bound_max:
                self.solution[i] = bound_max
            elif item < bound_min:
                self.solution[i] = bound_min

    def calculate_objective(self, objective_fun):
        """
        计算目标值
        :param objective_fun: 目标函数
        :return:
        """
        self.objective = objective_fun(self.solution)

    def __lt__(self, other):
        """
        重载小于号，只有当solution中全部小于对方，才判断小于
        :param other: 比较的个体
        :return: 1：小于 0：大于
        """
        v1 = list(self.objective.values())
        v2 = list(other.objective.values())
        for i in range(len(v1)):
            if v1[i] > v2[i]:
                return 0
        return 1

def fast_non_dominated_sort(P):
    """
    非支配排序
    :param P: 种群P
    :return: F：分层结果，返回值类型为dict，键为层号，值为list（该层中的个体）
    """
    F = defaultdict(list)

    for p in P:
        p.S = []
        p.n = 0
        for q in P:
            if p < q:       # p支配q
                p.S.append(q)
            elif q < p:     # q支配p
                p.n += 1
        if p.n == 0:
            p.rank = 1
            F[1].append(p)
    i = 1
    while F[i]:
        Q = []
        for p in F[i]:
            for q in p.S:
                q.n -= 1
                if q.n == 0:
                    q.rank = i + 1
                    Q.append(q)
        i += 1
        F[i] = Q
    return F

def crowding_distance_assignment(L):
    """
    计算拥挤度
    :param L: F[i]，是个list，为第i层的节点集合
    :return:
    """
    l = len(L)
    # 初始化距离
    for i in range(l):
        L[i].distance = 0
    # 遍历每个目标方向（有几个优化目标，就有几个目标方向）
    for m in L[0].objective.keys():
        L.sort(key=lambda x: x.objective[m])    # 使用objective值排序
        L[0].distance = float('inf')
        L[l - 1].distance = float('inf')
        f_max = L[l - 1].objective[m]
        f_min = L[0].objective[m]
        # 当某一个目标方向上的最大值和最小值相同时，会出现除0错误
        try:
            for i in range(1, l - 1):
                L[i].distance = L[i].distance + (L[i + 1].objective[m] - L[i - 1].objective[m]) / (f_max - f_min)
        except Exception:
            print(str(m) + "目标方向上，最大值为：" + str(f_max) + " 最小值为：" + str(f_min))

def binary_tornament(ind1, ind2):
    """
    二元锦标赛：先选非支配排序靠前的，再选拥挤度低（即距离远）；如果都不行，则随机
    :param ind1: 个体1
    :param ind2: 个体1
    :return: 返回较优的个体
    """
    if ind1.rank != ind2.rank:
        return ind1 if ind1.rank < ind2.rank else ind2
    elif ind1.distance != ind2.distance:
        return ind1 if ind1.distance > ind2.distance else ind2
    else:
        return ind1

def crossover_mutation(parent1, parent2, eta, bound_min, bound_max, objective_fun):
    """
    交叉：二进制交叉算子（SBX），变异：多项式变异（PM）
    :param parent1: 父代1
    :param parent2: 父代2
    :param eta: 变异参数，越大则后代个体越逼近父代
    :return:
    """
    poplength = len(parent1.solution)   # 解向量维数
    # 初始化两个后代个体
    offspring1 = Individual()
    offspring2 = Individual()
    offspring1.solution = np.empty(poplength)
    offspring2.solution = np.empty(poplength)
    # 二进制交叉
    for i in range(poplength):
        rand = random.random()
        if rand < 0.5:
            beta = (rand * 2) ** (1 / (eta + 1))
        else:
            beta = (1 / (2 * (1 - rand)))**(1 / (eta + 1))
        offspring1.solution[i] = 0.5 * ((1 + beta) * parent1.solution[i] + (1 - beta) * parent2.solution[i])
        offspring2.solution[i] = 0.5 * ((1 - beta) * parent1.solution[i] + (1 + beta) * parent2.solution[i])
    # 多项式变异
    for i in range(poplength):
        mu = random.random()
        if mu < 0.5:
            delta = 2 * mu ** (1 / (eta + 1))
        else:
            delta = (1 - (2 * (1 - mu)) ** (1 / (eta + 1)))
        # 只变异一个
        offspring1.solution[i] = offspring1.solution[i] + delta
    offspring1.bound_process(bound_min, bound_max)
    offspring2.bound_process(bound_min, bound_max)
    offspring1.calculate_objective(objective_fun)
    offspring2.calculate_objective(objective_fun)
    return [offspring1, offspring2]

def make_new_pop(P, eta, bound_min, bound_max, objective_fun):
    """
    选择交叉变异获得新后代
    :param P: 父代种群
    :param eta: 变异参数，越大则后代个体越逼近父代
    :param bound_min: 定义域下限
    :param bound_max: 定义域上限
    :param objective_fun: 目标函数
    :return: 子代种群
    """
    popnum = len(P)     # 种群个数
    Q = []
    # 二元锦标赛选择
    for i in range(int(popnum / 2)):
        # 从种群中随机选择两个个体，进行二元锦标赛，选择一个parent
        i = random.randint(0, popnum - 1)
        j = random.randint(0, popnum - 1)
        parent1 = binary_tornament(P[i], P[j])
        parent2 = parent1
        while (parent1.solution == parent2.solution).all():     # 小细节all
            i = random.randint(0, popnum - 1)
            j = random.randint(0, popnum - 1)
            parent2 = binary_tornament(P[i], P[j])
        Two_offspring = crossover_mutation(parent1, parent2, eta, bound_min, bound_max, objective_fun)
        Q.append(Two_offspring[0])
        Q.append(Two_offspring[1])
    return Q

def KUR(x):
    """
    计算各个目标方向上的目标值
    :param x: 解向量
    :return: 字典：各个方向上的目标值（key：目标方向；value：目标值）
    """
    f = defaultdict(float)
    poplength = len(x)
    f[1] = 0
    f[2] = 0
    for i in range(poplength - 1):
        f[1] = f[1] + (-10) * math.exp((-0.2) * (x[i] ** 2 + x[i + 1] ** 2) ** 0.5)
    for i in range(poplength):
        f[2] = f[2] + abs(x[i]) ** 0.8 + 5 * math.sin(x[i] ** 3)
    return f

def plot_P(P):
    """
    给种群绘图
    :param P: 种群集合
    :return:
    """
    X = []
    Y = []
    for ind in P:
        X.append(ind.objective[1])
        Y.append(ind.objective[2])
    plt.xlabel('F1')
    plt.ylabel('F2')
    plt.scatter(X, Y)

def main():
    # 初始化参数
    generations = 250   # 迭代次数
    popnum = 100        # 种群大小
    eta = 1             # 变异分布参数
    poplength = 3       # 单个个体解向量的维数
    bound_min = -5
    bound_max = 5
    objective_fun = KUR

    # 生成第一代种群
    P = []
    for i in range(popnum):
        P.append(Individual())
        P[i].solution = np.random.rand(poplength) * (bound_max - bound_min) + bound_min
        P[i].bound_process(bound_min, bound_max)    # 越界处理
        P[i].calculate_objective(objective_fun)     # 计算目标值

    # 快速非支配排序
    fast_non_dominated_sort(P)
    Q = make_new_pop(P, eta, bound_min, bound_max, objective_fun)
    P_t = P     # 当前这一代的父代种群
    Q_t = Q     # 当前这一代的子代种群
    for gen_cur in range(generations):
        R_t = P_t + Q_t
        F = fast_non_dominated_sort(R_t)
        P_n = []    # 即为P_t+1，表示下一代的父代
        i = 1
        # 依次将最高级别的支配平面中的节点放入到P_n中，之后更新非支配，直到达到要求的规模
        while len(P_n) + len(F[i]) < popnum:
            crowding_distance_assignment(F[i])
            P_n += F[i]
            i += 1
        # 按照支配排序选完之后，再按照拥挤度来选择
        F[i].sort(key=lambda x: x.distance)
        P_n = P_n + F[i][:popnum - len(P_n)]
        Q_n = make_new_pop(P_n, eta, bound_min, bound_max, objective_fun)

        # 将下一届的父代和子代成为当前的父代和子代
        P_t = P_n
        Q_t = Q_n

        # 可视化
        plt.clf()
        plt.title("current generation: " + str(gen_cur + 1))
        plot_P(P_t)
        plt.pause(0.1)

    plt.show()
    return 0



if __name__ == "__main__":
    main()

到了这里，关于NSGA-II 遗传多目标算法（python示例）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！